Sıradan en küçük kareler - Ordinary least squares

Bir serinin parçası
Regresyon analizi
Modeller
Doğrusal regresyon Basit regresyon polinom regresyon Genel doğrusal model
Genelleştirilmiş doğrusal model ayrık seçim Binom regresyon ikili regresyon Lojistik regresyon Çok terimli lojistik regresyon karışık logit yasaklamak çok terimli probit sıralı logit sıralı probit zehir
çok seviyeli model Sabit efektler rastgele efektler Doğrusal karışık efekt modeli Doğrusal olmayan karışık efekt modeli
Doğrusal olmayan regresyon Parametrik olmayan yarı parametrik güçlü Çeyreklik izotonik Ana bileşenleri en küçük açı Yerel parçalı
Değişkenlerdeki hatalar
Tahmin
En küçük kareler Doğrusal doğrusal olmayan
Sıradan Ağırlıklı genelleştirilmiş
Kısmi Toplam Negatif olmayan sırt regresyonu düzenli
En küçük mutlak sapmalar yinelemeli olarak yeniden ağırlıklandırılmış Bayes Bayes çok değişkenli
Arka plan
Regresyon doğrulama Ortalama ve tahmin edilen yanıt Hatalar ve artıklar Formda olmanın güzelliği Öğrencileştirilmiş kalıntı Gauss-Markov teoremi
matematik portalı
v T e

Olarak istatistik , sıradan en küçük kareler ( en küçük kareler ), bir tür azından doğrusal kareler bilinmeyen tahmin edilmesi için bir yöntem parametrelerinin bir de doğrusal regresyon modeli. OLS , bir dizi açıklayıcı değişkenin doğrusal bir fonksiyonunun parametrelerini en küçük kareler ilkesiyle seçer : verilen veri kümesinde gözlenen bağımlı değişken ( gözlenen değişkenin değerleri) ile tahmin edilenler arasındaki farkların karelerinin toplamını en aza indirgemek bağımsız değişkenin lineer fonksiyonu ile .

Geometrik olarak, bu, kümedeki her veri noktası ile regresyon yüzeyindeki karşılık gelen nokta arasındaki bağımlı değişkenin eksenine paralel olan uzaklıkların karesinin toplamı olarak görülür; farklar ne kadar küçükse, model verilere o kadar iyi uyar. . Ortaya çıkan tahmin edici , özellikle regresyon denkleminin sağ tarafında tek bir regresörün olduğu basit bir lineer regresyon durumunda basit bir formülle ifade edilebilir .

Olduğu tahmincisi EKK tutarlı önsavının olduğunda eksojen ve-by Gauss-Markov teoremi - lineer yansız tahmin edicilerin sınıfında optimum zaman hatalar vardır homoskedastik ve otokorelasyonsuz . Bu koşullar altında, OLS yöntemi , hatalar sonlu varyanslara sahip olduğunda minimum varyanslı ortalama yansız tahmin sağlar . Hataların normal dağıldığına dair ek varsayım altında , OLS maksimum olabilirlik tahmincisidir .

Doğrusal model

Verilerin gözlemlerden oluştuğunu varsayalım . Her gözlem skalar yanıtı içeren ve bir sütun vektörü içinde , yani parametreleri (önsavının), . Bir de doğrusal regresyon modeli , yanıt değişkeni, Regresörlerin doğrusal bir fonksiyonudur: ${\görüntüleme stili n}$ ${\displaystyle \sol\{\mathbf {x} _{i},y_{i}\sağ\}_{i=1}^{n}}$${\görüntüleme stili ben}$${\görüntüleme stili y_{i}}$${\displaystyle \mathbf {x} _{i}}$${\görüntüleme stili p}$${\displaystyle \mathbf {x} _{i}=\left[x_{i1},x_{i2},\dots ,x_{ip}\sağ]^{\mathsf {T}}}$${\görüntüleme stili y_{i}}$

${\displaystyle y_{i}=\beta _{1}\ x_{i1}+\beta _{2}\ x_{i2}+\cdots +\beta _{p}\ x_{ip}+\varepsilon _ {ben},}$

veya vektör biçiminde,

${\displaystyle y_{i}=\mathbf {x} _{i}^{\mathsf {T}}{\boldsymbol {\beta}}+\varepsilon _{i},\,}$

burada , daha önce tanıtıldığı gibi , tüm açıklayıcı değişkenlerin -th gözleminin bir sütun vektörüdür ; bilinmeyen parametrelerin bir vektörüdür; ve skaler , -th gözleminin gözlemlenmemiş rastgele değişkenlerini ( hataları ) temsil eder . açıklayıcılar dışındaki kaynaklardan gelen yanıtlar üzerindeki etkileri açıklar . Bu model ayrıca matris notasyonunda şu şekilde yazılabilir: ${\displaystyle \mathbf {x} _{i}}$${\görüntüleme stili ben}$${\ Displaystyle {\boldsymbol {\beta }}}$${\ Displaystyle p\times 1}$${\displaystyle \varepsilon _{i}}$${\görüntüleme stili ben}$${\displaystyle \varepsilon _{i}}$${\görüntüleme stili y_{i}}$${\displaystyle \mathbf {x} _{i}}$

${\displaystyle \mathbf {y} =\mathrm {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }},\,}$

burada ve vardır tepki değişkenleri vektörler ve hatalar gözlemler ve bir bir de de denir Regresör matrisi, tasarım matris Satır, olduğu ve ihtiva tüm açıklayıcı değişkenler inci gözlemler. ${\görüntüleme stili \mathbf {y} }$${\displaystyle {\boldsymbol {\varepsilon }}}$${\görüntüleme stili n\ kere 1}$${\görüntüleme stili n}$${\görüntüleme stili \mathrm {X} }$${\görüntüleme stili n\kez p}$${\görüntüleme stili ben}$${\displaystyle \mathbf {x} _{i}^{\mathsf {T}}}$${\görüntüleme stili ben}$

Kural olarak, sabit terim her zaman regresörler kümesine dahil edilir , örneğin all için alınır . Bu regresöre karşılık gelen katsayıya kesme denir . ${\görüntüleme stili \mathrm {X} }$${\displaystyle x_{i1}=1}$${\görüntüleme stili i=1,\noktalar,n}$${\görüntüleme stili \beta _{1}}$

Regresörlerin bağımsız olması gerekmez: Regresörler arasında arzu edilen herhangi bir ilişki olabilir (doğrusal bir ilişki olmadığı sürece). Örneğin, yanıtın hem bir değere hem de karesine doğrusal olarak bağlı olduğundan şüphelenebiliriz; bu durumda değeri başka bir regresörün karesi olan bir regresörü dahil edeceğiz. Bu durumda, model olacağını kuadratik ikinci regresör içinde, ama hiçbiri-az hala kabul edilir doğrusal modeli, çünkü modeli olan (parametrelerde hala çizgisel ). ${\ Displaystyle {\boldsymbol {\beta }}}$

Matris/vektör formülasyonu

Aşırı belirlenmiş bir sistem düşünün

${\displaystyle \sum _{j=1}^{p}X_{ij}\beta _{j}=y_{i},\ (i=1,2,\dots ,n),}$

arasında lineer denklem içinde bilinmeyen katsayılar , ile . (Not: yukarıdaki gibi bir lineer model için, içindeki tüm öğeler veri noktaları hakkında bilgi içermez. İlk sütun bir ile doldurulur, . Sadece diğer sütunlar gerçek verileri içerir. Yani burada regresör sayısı artı bire eşittir. ) Bu matris formunda şu şekilde yazılabilir:${\görüntüleme stili n}$ ${\görüntüleme stili p}$${\displaystyle \beta _{1},\beta _{2},\dots ,\beta _{p}}$${\displaystyle n>p}$${\görüntüleme stili \mathrm {X} }$${\displaystyle X_{i1}=1}$${\görüntüleme stili p}$

${\displaystyle \mathrm {X} {\boldsymbol {\beta }}=\mathbf {y} ,}$

nerede

${\displaystyle \mathrm {X} ={\başlangıç{bmatrix}X_{11}&X_{12}&\cdots &X_{1p}\\X_{21}&X_{22}&\cdots &X_{2p}\\\ vdots &\vdots &\ddots &\vdots \\X_{n1}&X_{n2}&\cdots &X_{np}\end{bmatrix}},\qquad {\boldsymbol {\beta }}={\başlangıç{bmatrix }\beta _{1}\\\beta _{2}\\\vdots \\\beta _{p}\end{bmatrix}},\qquad \mathbf {y} ={\begin{bmatrix}y_{ 1}\\y_{2}\\\vdots \\y_{n}\end{bmatrix}}.}$

Böyle bir sistemin genellikle kesin bir çözümü yoktur, bu nedenle amaç, ikinci dereceden minimizasyon problemini çözme anlamında "en iyi" denklemlere uyan katsayıları bulmaktır.${\ Displaystyle {\boldsymbol {\beta }}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}={\underset {\boldsymbol {\beta }}{\operatöradı {arg\,min} }}\,S({\boldsymbol {\beta }} ),}$

amaç fonksiyonunun verildiği yerde${\görüntüleme stili S}$

${\displaystyle S({\boldsymbol {\beta }})=\sum _{i=1}^{n}{\biggl |}y_{i}-\sum _{j=1}^{p}X_ {ij}\beta _{j}{\biggr |}^{2}={\bigl \|}\mathbf {y} -\mathrm {X} {\boldsymbol {\beta }}{\bigr \|} ^{2}.}$

Bu kriteri seçme gerekçesi aşağıdaki Özellikler'de verilmiştir. Bu minimize etme sorunu da koşuluyla, tek bir çözümü vardır matrisin sütunları olan lineer bağımsız çözerek verilen normal bir denklem${\görüntüleme stili p}$${\görüntüleme stili \mathrm {X} }$

${\displaystyle (\mathrm {X} ^{\mathsf {T}}\mathrm {X} ){\hat {\boldsymbol {\beta }}}=\mathrm {X} ^{\mathsf {T}}\ matematikbf {y} \ .}$

Matris olarak bilinen Gram matris ve matris olarak bilinen an matris Regresörlerin regressand arasında. Son olarak, en küçük kareler hiperdüzleminin katsayı vektörü şu şekilde ifade edilir: ${\displaystyle \mathrm {X} ^{\mathsf {T}}\mathrm {X} }$${\displaystyle \mathrm {X} ^{\mathsf {T}}\mathbf {y} }$${\displaystyle {\hat {\boldsymbol {\beta }}}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}=\left(\mathrm {X} ^{\mathsf {T}}\mathrm {X} \sağ)^{-1}\mathrm {X} ^{\mathsf {T}}\mathbf {y} .}$

veya

${\displaystyle {\hat {\boldsymbol {\beta }}}={\boldsymbol {\beta }}+(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf { X} ^{\top }{\boldsymbol {\varepsilon }}.}$

Tahmin

b'nin β parametre vektörü için bir "aday" değer olduğunu varsayalım . Miktarı y _ı - X _i ^{, T} B adı verilen kalıntı için i veri noktası arasındaki önlemler düşey mesafe, inci gözlem ( x _i , y _i ) ve hiper y = x ^T B , ve böylece derecesini ölçmek gerçek veriler ve model arasında uyum sağlar. Kare toplamlarının ( SSR ) (ayrıca kareler hata toplamı ( ESS ) ya da rezidüel kareler toplamı ( RSS )) bu model, uyum bir ölçüsüdür:

${\displaystyle S(b)=\sum _{i=1}^{n}(y_{i}-x_{i}^{\mathrm {T} }b)^{2}=(y-Xb) ^{\mathrm {T} }(y-Xb),}$

burada T matris devriğini gösterir ve X satırları , bağımlı değişkenin belirli bir değeriyle ilişkili tüm bağımsız değişkenlerin değerlerini belirtir, X _i = x _i ^T'dir . Bu toplamı minimize eden b değerine β için OLS tahmincisi denir . S ( b ) işlevi , b'de pozitif tanımlı Hessian ile ikinci derecedendir ve bu nedenle bu işlev , açık formülle verilebilecek benzersiz bir global minimuma sahiptir : ^[kanıt]${\displaystyle b={\hat {\beta }}}$

${\displaystyle {\hat {\beta }}=\operatör adı {argmin} _{b\in \mathbb {R} ^{p}}S(b)=(X^{\mathrm {T} }X)^ {-1}X^{\mathrm {T} }y\ .}$

Ürün K = X ^{, T} x a, gram matris ve tersi, Q, = N ^-1 , bir kofaktör matrisi arasında p yakından ilişkili, kovaryans matrisinin , Cı- _P . ( X ^T X ) ^–1 X ^T = Q X ^T matrisi, X'in Moore-Penrose sözde -ters matrisi olarak adlandırılır. Bu formülasyon, tahminin ancak ve ancak, aralarında mükemmel bir çoklu doğrusal bağlantı olmaması durumunda gerçekleştirilebileceğini vurgular . açıklayıcı değişkenler (ki bu, gram matrisinin tersi olmamasına neden olur).

Olduğunu tahmin sonra β , edilen değeri (ya da öngörülen değerler regresyonundan) olacaktır

${\displaystyle {\hat {y}}=X{\hat {\beta }}=Py,}$

burada P = X ( X ^T X ) ⁻¹ X ^T , X'in sütunları tarafından yayılan V uzayına izdüşüm matrisidir . Bu matris P aynı zamanda bazen şapka matrisi olarak da adlandırılır çünkü y değişkenine "bir şapka koyar" . P ile yakından ilişkili başka bir matris, yok edici matristir M = I _n − P ; bu, V'ye dik uzay üzerine bir izdüşüm matrisidir . Hem matris P ve M olan simetrik ve İdempotent (yani P ² = P ve M ² = E ve veri matrisi ile ilgilidir) X kimlikleri ile PX = X ve MX = 0 . Matrix M , regresyondan kalanları oluşturur :

${\displaystyle {\hat {\varepsilon }}=y-{\hat {y}}=yX{\hat {\beta }}=My=M(X\beta +\varepsilon )=(MX)\beta + M\varepsilon =M\varepsilon .}$

Bu artıkları kullanarak, indirgenmiş ki-kare istatistiğini kullanarak σ ² değerini tahmin edebiliriz :

${\displaystyle s^{2}={\frac {{\hat {\varepsilon }}^{\mathrm {T} }{\hat {\varepsilon }}}{np}}={\frac {(Benim) ^{\mathrm {T} }Benim}{np}}={\frac {y^{\mathrm {T} }M^{\mathrm {T} }Benim}{np}}={\frac {y^ {\mathrm {T} }My}{np}}={\frac {S({\hat {\beta }})}{np}},\qquad {\hat {\sigma }}^{2}= {\frac {np}{n}}\;s^{2}}$

Payda, n - p , istatistiksel serbestlik derecesidir . İlk nicelik, s ² , σ ² için OLS tahmini iken, ikincisi, , σ ² için MLE tahminidir . Büyük örneklerde iki tahmin edici oldukça benzerdir; İlk tahmincisi daima edilir tarafsız ikinci tahmincisi önyargılı iken, ancak daha küçük sahiptir ortalama karesel hata . Uygulamada s ² , hipotez testi için daha uygun olduğu için daha sık kullanılır. Karekökü s ² olarak adlandırılır regresyon standart hata , regresyon standart hata , veya denklemin standart hata . ${\displaystyle \scriptstyle {\hat {\sigma }}^{2}}$

OLS regresyonunun uyum iyiliğini, X'e gerileyerek örnekteki ilk varyasyonun ne kadar azaltılabileceğini karşılaştırarak değerlendirmek yaygındır . Belirleme katsayısı R ² bağımlı değişken bir "toplam" varyansa varyans "açıklandığı" bir oranı olarak tanımlanır y kareler regresyon toplamı artıkların karelerinin toplamı eşittir durumlarda:

${\displaystyle R^{2}={\frac {\sum ({\hat {y}}_{i}-{\overline {y}})^{2}}{\sum (y_{i}-) {\overline {y}})^{2}}}={\frac {y^{\mathrm {T} }P^{\mathrm {T} }LPy}{y^{\mathrm {T} }Ly }}=1-{\frac {y^{\mathrm {T} }My}{y^{\mathrm {T} }Ly}}=1-{\frac {\rm {RSS}}{\rm { TS}}}}$

burada TSS, bağımlı değişken için karelerin toplam toplamıdır ve bir n × n matrisidir. ( bir sabit üzerindeki regresyona eşdeğer bir merkezleme matrisidir ; sadece bir değişkenden ortalamayı çıkarır.) R ^2'nin anlamlı olması için, regresörler üzerindeki verilerin X matrisi, aşağıdakileri temsil edecek bir sütun vektörü içermelidir. katsayısı regresyon kesişimi olan sabit. Bu durumda, R ' ² , her zaman değerleri uyum iyi derecede gösteren 1'e yakın olan, 0 ile 1 arasında bir sayı olacaktır. ${\textstyle L=I_{n}-{\frac {1}{n}}J_{n}}$${\textstyle J_{n}}$${\görüntüleme stili L}$

Bağımsız değişkenin bağımlı değişkenin bir fonksiyonu olarak tahminindeki varyans, Polinom en küçük kareler makalesinde verilmiştir .

Basit doğrusal regresyon modeli

X veri matrisi yalnızca iki değişken, bir sabit ve bir skaler regresör x _i içeriyorsa , buna "basit regresyon modeli" denir. Bu durum, manuel hesaplama için bile uygun olan çok daha basit formüller sağladığından, genellikle başlangıç ​​istatistik sınıflarında dikkate alınır. Parametreler genel olarak ( α , β ) olarak belirtilir :

${\displaystyle y_{i}=\alpha +\beta x_{i}+\varepsilon _{i}.}$

Bu durumda en küçük kareler tahminleri basit formüllerle verilir.

${\displaystyle {\begin{hizalanmış}{\hat {\beta }}&={\frac {{n}\sum {x_{i}y_{i}}-\sum {x_{i}}\sum { y_{i}}}{{n}\sum {x_{i}^{2}}-(\sum {x_{i}})^{2}}}\\{\hat {\alpha }}& ={\overline {y}}-{\hat {\beta }}\,{\overline {x}}\ ,\end{hizalı}}}$

alternatif türevler

Bir önceki bölümde en küçük kareler tahmincisi , modelin artık karelerinin toplamını minimize eden bir değer olarak elde edilmiştir. Ancak aynı tahmin ediciyi diğer yaklaşımlardan da elde etmek mümkündür. Her durumda OLS tahmincisi formülü aynı kalır: ^{^} β = ( X ^T X ) ⁻¹ X ^T y ; tek fark, bu sonucu nasıl yorumladığımızdır. ${\ Displaystyle {\hat {\beta }}}$

Projeksiyon

Matematikçiler için, OLS, β'nın bilinmeyen olduğu Xβ ≈ y aşırı belirlenmiş bir lineer denklem sistemine yaklaşık bir çözümdür . Sistemini varsayarsak (denklem sayısı tam olarak çözülemez n bilinmeyenler sayısının çok daha büyüktür p ), biz sağ ve sol yön tarafı arasında en küçük tutarsızlığı sağlayabilir çözüm aramaktadır. Başka bir deyişle, tatmin edici bir çözüm arıyoruz.

${\displaystyle {\hat {\beta }}={\rm {arg}}\min _{\beta }\,\lVert yX\beta \rVert,}$

nerede ||·|| standart L ²  normu içinde n- boyutlu Öklid alan R ^{, n} . Tahmin edilen Xβ miktarı , sadece regresör vektörlerinin belirli bir lineer birleşimidir. Bu nedenle, artık vektör y - Xβ küçük uzunluğa sahip olacaktır y olan dikey olarak yansıtılan üzerine lineer alt uzay yayılmış ve sütunlara göre X . OLS tahmin bu durumda katsayıları olarak yorumlanabilir vektör ayrışma içinde ^{^} y = Py temelinde boyunca X . ${\ Displaystyle {\hat {\beta }}}$

Başka bir deyişle, minimumdaki gradyan denklemleri şu şekilde yazılabilir:

${\displaystyle (\mathbf {y} -X{\hat {\boldsymbol {\beta }}})^{\rm {T}}X=0.}$

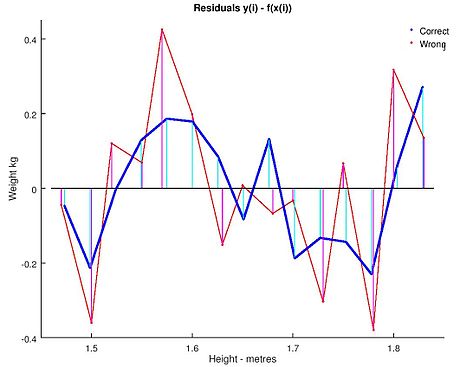
Bu denklemler bir geometrik yorumu artıkların vektörü, yani ortogonal olan kolon alanı arasında X nokta ürün için, sıfıra eşit olduğu bir konformal vektörü, v . Bu , mümkün olan tüm vektörlerin en kısasının olduğu anlamına gelir , yani artıkların varyansı mümkün olan en düşük değerdir. Bu sağda gösterilmiştir. ${\displaystyle \mathbf {y} -X{\hat {\boldsymbol {\beta }}}}$${\displaystyle (\mathbf {y} -X{\hat {\boldsymbol {\beta }}})\cdot X\mathbf {v} }$${\displaystyle \mathbf {y} -X{\boldsymbol {\hat {\beta }}}}$${\displaystyle \mathbf {y} -X{\boldsymbol {\beta }}}$

Bir matrisin tekil olmadığı ve K ^T X = 0 (cf. Ortogonal projeksiyonlar ) varsayımıyla bir K matrisi tanıtıldığında , artık vektör aşağıdaki denklemi sağlamalıdır: ${\displaystyle {\hat {\boldsymbol {\gamma }}}}$${\görüntüleme stili [X\ K]}$

${\displaystyle {\hat {\mathbf {r} }}\triangleq \mathbf {y} -X{\hat {\boldsymbol {\beta }}}=K{\hat {\boldsymbol {\gamma }}}. }$

Doğrusal en küçük karelerin denklemi ve çözümü aşağıdaki gibi tanımlanır:

${\displaystyle \mathbf {y} ={\begin{bmatrix}X&K\end{bmatrix}}{\begin{pmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {\ gama }}}\end{pmatrix}},}$

${\displaystyle {\begin{pmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {\gamma }}}\end{pmatrix}}={\begin{bmatrix}X&K\ bitiş{bmatrix}}^{-1}\mathbf {y} ={\başlangıç{bmatrix}(X^{\rm {T}}X)^{-1}X^{\rm {T}}\\ (K^{\rm {T}}K)^{-1}K^{\rm {T}}\end{bmatrix}}\mathbf {y} .}$

Buna bakmanın başka bir yolu, regresyon çizgisini, veri kümesindeki herhangi iki noktanın birleşiminden geçen çizgilerin ağırlıklı ortalaması olarak düşünmektir. Bu hesaplama yöntemi, hesaplama açısından daha pahalı olmasına rağmen, OLS üzerinde daha iyi bir sezgi sağlar.

Maksimum olasılık

OLS tahmincisi, hata terimleri için normallik varsayımı altında maksimum olabilirlik tahmincisi (MLE) ile aynıdır . ^[kanıt] Bu normallik varsayımı tarihsel öneme sahiptir, çünkü Yule ve Pearson tarafından lineer regresyon analizindeki erken çalışma için temel sağlar . MLE'nin özelliklerinden , normallik varsayımı karşılanırsa , OLS tahmincisinin asimptotik olarak verimli olduğunu ( varyans için Cramér-Rao sınırına ulaşma anlamında) çıkarabiliriz .

Genelleştirilmiş moment yöntemi

Gelen iid durumda en küçük kareler tahmincisi olarak ta görülebilir GMM zaman şartlarının kaynaklanan tahmin

${\displaystyle \mathrm {E} {\big [}\,x_{i}(y_{i}-x_{i}^{T}\beta )\,{\big ]}=0.}$

Bu moment koşulları, regresörlerin hatalarla ilişkisiz olması gerektiğini belirtir. Yana x _i a, p -vector, zaman şartlarının sayısı parametre vektörü boyutuna eşit olan p ve böylece sistem tam olarak tanımlanır. Bu, tahmin edicinin ağırlıklandırma matrisinin seçimine bağlı olmadığı klasik GMM durumudur.

Orijinal katı dışsallık varsayımının E[ ε _i  | x _i ] = 0 , yukarıda belirtilenden çok daha zengin bir moment koşulları kümesi anlamına gelir. Özellikle, bu varsayım, herhangi bir vektör fonksiyonu ƒ için , E[ ƒ ( x _i )· ε _i ] = 0 moment koşulunun geçerli olacağını ima eder . Bununla birlikte, ƒ fonksiyonunun optimal seçiminin ƒ ( x ) = x almak olduğu Gauss-Markov teoremi kullanılarak gösterilebilir , bu da yukarıda verilen moment denklemiyle sonuçlanır.

Özellikler

varsayımlar

OLS tekniğini uygulanabilir kılmak için doğrusal regresyon modelinin oluşturulabileceği birkaç farklı çerçeve vardır . Bu ayarların her biri aynı formülleri ve aynı sonuçları üretir. Tek fark, yöntemin anlamlı sonuçlar vermesi için uygulanması gereken yorum ve varsayımlardır. Uygulanabilir çerçevenin seçimi, çoğunlukla eldeki verilerin doğasına ve gerçekleştirilmesi gereken çıkarım görevine bağlıdır.

Yorumdaki farklılık çizgilerinden biri, regresörlerin rastgele değişkenler olarak mı yoksa önceden tanımlanmış sabitler olarak mı ele alınacağıdır. İlk durumda ( rasgele tasarım ) önsavının x _i , rastgele ve birlikte örneklenmiş olan y _ı 'bazı s nüfus bir olduğu gibi, gözlem çalışma . Bu yaklaşım , tahmin edicilerin asimptotik özelliklerinin daha doğal çalışmasına izin verir . Diğer yorumlamada ( sabit tasarım ), X regresörleri bir tasarım tarafından belirlenen bilinen sabitler olarak ele alınır ve y , bir deneyde olduğu gibi X değerlerine göre koşullu olarak örneklenir . Pratik amaçlar için, bu ayrım genellikle önemsizdir, çünkü tahmin ve çıkarım, X üzerinde koşullandırma sırasında yürütülür . Bu makalede belirtilen tüm sonuçlar rastgele tasarım çerçevesi içindedir.

Klasik doğrusal regresyon modeli

Klasik model, "sonlu örnek" tahmini ve çıkarımına odaklanır, yani gözlem sayısı n sabittir. Bu, OLS'nin asimptotik davranışını inceleyen ve gözlem sayısının sonsuza kadar büyümesine izin verilen diğer yaklaşımlarla çelişir .

• Doğru şartname . Doğrusal işlevsel biçim, gerçek veri oluşturma sürecinin biçimiyle örtüşmelidir.
• Katı dışsallık . Regresyondaki hatalar koşullu ortalama sıfıra sahip olmalıdır :

  ${\displaystyle \operatöradı {E} [\,\varepsilon \mid X\,]=0.}$

Dışsallık varsayımının hemen sonucu, hataların ortalama sıfıra sahip olması: E[ ε ] = 0 ve regresörlerin hatalarla ilişkisiz olmasıdır: E[ X ^T ε ] = 0 .

OLS teorisi için dışsallık varsayımı kritik öneme sahiptir. Tutarsa, regresör değişkenlere eksojen denir . Olmazsa, hata terimiyle ilişkili olan regresörlere endojen denir ve OLS tahminleri geçersiz olur. Böyle bir durumda, çıkarımı gerçekleştirmek için araç değişkenler yöntemi kullanılabilir.

• Doğrusal bağımlılık yok . X'teki regresörlerin tümü lineer olarak bağımsız olmalıdır . Matematiksel olarak bu, X matrisinin neredeyse kesin olarak tam sütun sıralamasına sahip olması gerektiği anlamına gelir :

  ${\displaystyle \Pr \!{\big [}\,\operatöradı {rütbe} (X)=p\,{\big ]}=1.}$

Genellikle, regresörlerin en azından ikinci momente kadar sonlu momentleri olduğu da varsayılır. O halde Q _xx = E[ X ^T X  /  n ] matrisi sonlu ve pozitif yarı tanımlıdır.

Bu varsayım ihlal edildiğinde, regresörlere doğrusal bağımlı veya mükemmel çoklu doğrusal bağlantı denir . Bu durumda , aynı lineer bağımlı alt uzayda bulunan regresörlerin yeni değerleri için y değerlerinin tahmini hala mümkün olsa da , regresyon katsayısının β değeri öğrenilemez .

• Küresel hatalar :

  ${\displaystyle \operatöradı {Var} [\,\varepsilon \mid X\,]=\sigma ^{2}I_{n},}$

burada I _{, n} olan birim matris boyutta , n ve σ ² , her gözlem varyansını belirleyen bir parametredir. Bu σ ² , genellikle tahmin edilmesine rağmen, modelde rahatsız edici bir parametre olarak kabul edilir . Bu varsayım ihlal edilirse, OLS tahminleri hala geçerlidir, ancak artık verimli değildir.

Bu varsayımı iki bölüme ayırmak gelenekseldir:

• Homoscedasticity : E[  ε _i ²  | X  ] = σ ² , bu, hata terimininher gözlemdeaynı varyansa σ ² sahip olduğu anlamına gelir. Bu gereklilik ihlal edildiğinde buna değişen varyans denir, böyle bir durumda daha verimli bir tahmin edici ağırlıklı en küçük kareler olacaktır . Hatalar sonsuz varyansa sahipse, OLS tahminleri de sonsuz varyansa sahip olacaktır (her ne kadar büyük sayılar yasasına göre hatalar sıfır ortalamaya sahip olduğu sürece yine de gerçek değerlere yöneleceklerdir). Bu durumda, sağlam tahmin teknikleri önerilir.
• Otokorelasyon yok : hatalar gözlemler arasında korelasyonsuzdur : E[  ε _i ε _j  | i ≠ j için X  ] = 0 . Bu varsayım, zaman serisi verileri, panel verileri , küme örnekleri, hiyerarşik veriler, tekrarlanan ölçüm verileri, boylamsal veriler ve bağımlı diğer veriler bağlamında ihlal edilebilir . Bu gibi durumlarda genelleştirilmiş en küçük kareler , OLS'den daha iyi bir alternatif sağlar. Otokorelasyon için başka bir ifade seri korelasyondur .

• Normallik . Bazen ek olarak, hataların regresörlere bağlı olarak normal dağılıma sahip olduğu varsayılır :

  ${\displaystyle \varepsilon \mid X\sim {\mathcal {N}}(0,\sigma ^{2}I_{n}).}$

Bu varsayım, OLS yönteminin geçerliliği için gerekli değildir, ancak gerekli olduğu durumda (özellikle hipotez testleri alanında) bazı ek sonlu örnek özellikleri oluşturulabilir. Ayrıca hatalar normal olduğunda, OLS tahmincisi maksimum olabilirlik tahmincisine (MLE) eşdeğerdir ve bu nedenle tüm düzenli tahmin ediciler sınıfında asimptotik olarak etkindir . Daha da önemlisi, normallik varsayımı yalnızca hata terimleri için geçerlidir; Popüler bir yanılgının aksine, yanıt (bağımlı) değişkeninin normal dağılması gerekli değildir.

Bağımsız ve aynı şekilde dağıtılmış (iid)

Bazı uygulamalarda, özellikle enine kesit verileriyle , ek bir varsayım uygulanır - tüm gözlemler bağımsız ve aynı şekilde dağıtılır. Bu, tüm gözlemlerin, daha önce listelenen tüm varsayımları daha basit ve yorumlanmasını kolaylaştıran rastgele bir örnekten alındığı anlamına gelir . Ayrıca bu çerçeve , veri üretme sürecinden yeni bağımsız gözlemler getirmenin teorik bir olasılığı olarak anlaşılan asimptotik sonuçların (örnek boyutu n  → ∞ olarak ) belirtilmesine izin verir . Bu durumda varsayımların listesi:

• iid gözlemler : ( x _ben , y _ben ) tüm i ≠ j için ( x _j , y _j ) ' den bağımsızdır ve aynı dağılıma sahiptir ;
• Hiçbir mükemmel çoklu doğrusal : Q, _xx = E [  x _i  x _i ^T  ] a, pozitif tanımlı bir matris ;
• dışsallık : E[  ε _i  | x _ben  ] = 0;
• homoscedasticity : Var[  ε _i  | x _ben  ] = σ ² .

Zaman serisi modeli

• Stokastik işlem { x _i , y _i } olan sabit ve ergodik ; { x _i , y _ben } durağan değilse, { x _i , y _ben } birlikte bütünleşmediği sürece OLS sonuçları genellikle sahtedir .
• Regresörler önceden belirlenir : tüm i = 1, ..., n için E[ x _ben ε _ben ] = 0 ;
• P x s matrisi S _xx = E [  x _i  x _i ^T  ] tam sıralı olan ve bu nedenle pozitif tanımlı ;
• { x _i ε _ben } ikinci momentlerin sonlu matrisi olan bir martingale fark dizisidir Q _{xxε ²} = E[  ε _ben ² x _ben  x _ben ^T  ] .

Sonlu örnek özellikleri

Altında Öncelikle sıkı eksojenite varsayımı EKK tahmin edicileri ve s ² olan tarafsız beklenen değerler parametrelerin gerçek değerleri ile çakışacak yani: ^[geçirmez]${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatöradı {E} [\,{\hat {\beta }}\mid X\,]=\beta ,\quad \operatöradı {E} [\,s^{2}\mid X\,] =\sigma ^{2}.}$

Katı dışsallık geçerli değilse (birçok zaman serisi modelinde olduğu gibi, dışsallığın yalnızca geçmiş şoklara göre varsayıldığı ancak gelecekteki şoklara göre değil), bu tahminciler sonlu örneklerde yanlı olacaktır.

Varyans-kovaryans matrisi (veya basitçe kovaryans matrisi ) arasında eşittir ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {Var} [\,{\hat {\beta }}\mid X\,]=\sigma ^{2}(X^{T}X)^{-1}=\sigma ^{ 2}S.}$

Özellikle, her katsayının standart hatası , bu matrisin j -inci köşegen elemanının kareköküne eşittir . Bu standart hatanın tahmini, bilinmeyen σ ² miktarının tahmini s ² ile değiştirilmesiyle elde edilir . Böylece, ${\displaystyle \scriptstyle {\hat {\beta }}_{j}}$

${\displaystyle {\widehat {\operatöradı {s.\!e.} }}({\hat {\beta }}_{j})={\sqrt {s^{2}(X^{T}X) )_{jj}^{-1}}}}$

Tahmin edicinin modelden kalanlarla ilişkisiz olduğu da kolayca gösterilebilir : ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatöradı {Cov} [\,{\hat {\beta }},{\hat {\varepsilon }}\mid X\,]=0.}$

Gauss-Markov teoremi altında olduğunu belirtmektedir küresel hatalar varsayımı (olduğunu, hatalar olmalı ilintisiz ve homoskedastik tahmincisi) lineer yansız tahmin edicilerin sınıfında etkilidir. Buna en iyi doğrusal yansız tahmin edici (MAVİ) denir . Bunu başka tahmincisi bulmak için sanki Verimlilik anlaşılmalıdır lineer olacağını y ve tarafsız ardından, ${\displaystyle \scriptstyle {\hat {\beta }}}$${\displaystyle \scriptstyle {\tilde {\beta }}}$

${\displaystyle \operatöradı {Var} [\,{\tilde {\beta }}\mid X\,]-\operatöradı {Var} [\,{\hat {\beta }}\mid X\,]\geq 0}$

Bu, negatif-tanımlı olmayan bir matris olması anlamında . Bu teorem, optimalliği yalnızca oldukça kısıtlayıcı olan doğrusal yansız tahmin ediciler sınıfında kurar. Hata terimlerinin dağılımına bağlı olarak ε , diğer doğrusal olmayan tahmin ediciler OLS'den daha iyi sonuçlar verebilir.

normallik varsayarsak

Şimdiye kadar listelenen özelliklerin tümü, hata terimlerinin altında yatan dağılımdan bağımsız olarak geçerlidir. Ancak, normallik varsayımının geçerli olduğunu varsaymaya istekliyseniz (yani, ε ~ N (0, σ ² I _n ) ), o zaman OLS tahmincilerinin ek özellikleri belirtilebilir.

Tahmin edici , daha önce verildiği gibi ortalama ve varyansla normal olarak dağıtılır: ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle {\hat {\beta }}\ \sim \ {\mathcal {N}}{\big (}\beta ,\ \sigma ^{2}(X^{\mathrm {T} }X)^) {-1}{\büyük )}}$

burada Q , kofaktör matrisidir . Bu tahmin edici , model için Cramér-Rao sınırına ulaşır ve bu nedenle tüm yansız tahmin ediciler sınıfında optimaldir. Gauss-Markov teoreminin aksine , bu sonucun hem lineer hem de lineer olmayan tahmin ediciler arasında optimalliği oluşturduğuna, ancak sadece normal dağılmış hata terimleri durumunda olduğuna dikkat edin.

Tahmin edici s ² , ki-kare dağılımıyla orantılı olacaktır :

${\displaystyle s^{2}\ \sim \ {\frac {\sigma ^{2}}{np}}\cdot \chi _{np}^{2}}$

Bu tahmin varyansı eşittir 2 σ ⁴ / ( n  -  p ) , elde etmeyen Cramer-Rao bağlanmış bir 2 σ ⁴ / n . Ancak , varyansı s ² kestiricisinden daha küçük olan σ ^2'nin yansız kestiricilerinin olmadığı gösterilmiştir . Önyargılı tahmincilere izin vermeye istekliysek ve modelin karesel artıklarının (SSR) toplamı ile orantılı tahmin edici sınıfını göz önünde bulundurursak, bu sınıftaki en iyi ( ortalama kare hatası anlamında ) tahmin edici olacaktır. ^~ σ ² = SSR  /  ( n  −  p  + 2) , bu, yalnızca bir regresör ( p = 1 ) olduğunda Cramér–Rao sınırını bile geçer .

Ayrıca, tahmin ve s ² olan , bağımsız , regresyon için T ve F-test yapımında yararlıdır gelir aslında. ${\displaystyle \scriptstyle {\hat {\beta }}}$

Etkili gözlemler

Daha önce olduğu gibi sözü edilen tahmin edici lineerdir y bağımlı değişkenlerin lineer kombinasyonu temsil eder, yani, y _i . Bu lineer kombinasyondaki ağırlıklar, X regresörlerinin fonksiyonlarıdır ve genellikle eşit değildir. Yüksek ağırlıklı gözlemler , tahmin edicinin değeri üzerinde daha belirgin bir etkiye sahip oldukları için etkili olarak adlandırılır . ${\ Displaystyle {\hat {\beta }}}$

Biz belirli kaldırmak etkili olan gözlemler analiz etmek j -inci gözlem ve tahmini miktarlar (benzer Değişikliğin olacak ne kadar dikkate sustalı çakı yöntemiyle ). β için OLS tahmin edicisindeki değişimin şuna eşit olacağı gösterilebilir.

${\displaystyle {\hat {\beta }}^{(j)}-{\hat {\beta }}=-{\frac {1}{1-h_{j}}}(X^{\mathrm { T} }X)^{-1}x_{j}^{\mathrm {T} }{\hat {\varepsilon }}_{j}\,,}$

burada h _j = x _j ^T  ( X ^T X ) ⁻¹ x _j , şapka matrisinin P'nin j -inci köşegen elemanıdır ve x _j , j -inci gözleme karşılık gelen regresörlerin vektörüdür . Benzer bir şekilde, tahmin edilen değer değişiklik j veri kümesinden bu gözlemi atlama kaynaklanan-inci gözlem eşit olacaktır

${\displaystyle {\hat {y}}_{j}^{(j)}-{\hat {y}}_{j}=x_{j}^{\mathrm {T} }{\hat {\ beta }}^{(j)}-x_{j}^{T}{\hat {\beta }}=-{\frac {h_{j}}{1-h_{j}}}\,{\ şapka {\varepsilon }}_{j}}$

Şapka matrisinin özelliklerinden, 0 ≤ h _j ≤ 1 ve toplamları p'ye eşittir , böylece ortalama olarak h _j ≈ p/n . Bu miktarlar h _j denir kaldıraç ve yüksek olan gözlemler h _j denir kaldıraç noktalarını . Genellikle, yüksek kaldıraçlı gözlemler, hatalı olmaları, aykırı olmaları veya başka bir şekilde veri kümesinin geri kalanının atipik olması durumunda daha dikkatli bir şekilde incelenmelidir.

bölümlenmiş regresyon

Bazen regresyondaki değişkenler ve karşılık gelen parametreler mantıksal olarak iki gruba ayrılabilir, böylece regresyon şekillenir.

${\displaystyle y=X_{1}\beta _{1}+X_{2}\beta _{2}+\varepsilon,}$

burada X, ₁ ve X, ₂ boyutlara sahip , n x s ₁ , n x P ₂ ve β ₁ , β ₂ olan p ₁ x 1 ve p ₂ ile x 1 vektörler, s ₁ + p ₂ = s .

Frisch-Waugh-Lovell teoremi bu regresyon artıklar belirtmektedir ve en küçük kareler tahmin artıklar sayısal aynı olacaktır ve en küçük kareler için tahmin p ₂ , aşağıdaki regresyon: ${\displaystyle {\hat {\varepsilon }}}$${\displaystyle \scriptstyle {\hat {\beta }}_{2}}$

${\displaystyle M_{1}y=M_{1}X_{2}\beta _{2}+\eta \,,}$

burada M ₁ olduğu Yokedici matris regresyonu x ₁ .

Teorem, bir dizi teorik sonuç oluşturmak için kullanılabilir. Örneğin, bir sabit ve başka bir regresör ile bir regresyona sahip olmak, bağımlı değişkenden ve regresörden ortalamaları çıkarmaya ve ardından regresyonu, sabit terim olmadan, anlamı azaltılmış değişkenler için çalıştırmaya eşdeğerdir.

kısıtlı tahmin

Regresyondaki katsayıların bir lineer denklem sistemini sağladığının bilindiğini varsayalım.

${\displaystyle A\colon \quad Q^{T}\beta =c,\,}$

burada Q , tam sıralı bir p × q matrisidir ve c , bilinen sabitlerin bir q × 1 vektörüdür, burada q < p . Bu durumda, en küçük kareler tahmini, A kısıtına tabi olan modelin artık karelerinin toplamının minimizasyonuna eşdeğerdir . Kısıtlı en küçük kareler (CLS) tahmin açık bir formül verilebilir:

${\displaystyle {\hat {\beta }}^{c}={\hat {\beta }}-(X^{T}X)^{-1}Q{\Big (}Q^{T}( X^{T}X)^{-1}Q{\Big )}^{-1}(Q^{T}{\hat {\beta }}-c).}$

Kısıtlı tahmin edici için bu ifade, X ^T X matrisi ters çevrilebilir olduğu sürece geçerlidir . Bu makalenin başından itibaren bu matrisin tam ranklı olduğu varsayıldı ve rank koşulu başarısız olduğunda β'nın tanımlanamayacağı belirtildi. Bununla birlikte, A kısıtlamasının eklenmesi β'yı tanımlanabilir hale getirebilir , bu durumda tahmin edicinin formülünü bulmak istenir. Tahminci şuna eşittir:

${\displaystyle {\hat {\beta }}^{c}=R(R^{T}X^{T}XR)^{-1}R^{T}X^{T}y+{\Büyük ( }I_{p}-R(R^{T}X^{T}XR)^{-1}R^{T}X^{T}X{\Big )}Q(Q^{T}Q) ^{-1}c,}$

burada R bir p ×( p  −  q ) matrisidir, öyle ki [ QR ] matrisi tekil değildir ve R ^T Q = 0 . Böyle bir matris her zaman bulunabilir, ancak genellikle benzersiz değildir. X ^T X'in ters çevrilebilir olması durumunda ikinci formül birinciyle çakışır .

Büyük numune özellikleri

En küçük kareler tahmin edicileri , doğrusal regresyon modeli parametrelerinin β nokta tahminleridir . Bununla birlikte, genellikle bu tahminlerin, parametrelerin gerçek değerlerine ne kadar yakın olabileceğini de bilmek isteriz. Başka bir deyişle, aralık tahminlerini oluşturmak istiyoruz .

Biz hata teriminin dağılımı hakkında herhangi tahmininde bulunmayan yana ε _i , tahmin edicilerin dağılımını anlaması mümkün değildir ve . Yine de, örneklem büyüklüğü n sonsuza giderken asimptotik özelliklerini türetmek için merkezi limit teoremini uygulayabiliriz . Örnek boyutu zorunlu olarak sonlu olsa da , OLS tahmincisinin gerçek dağılımının asimptotik sınırına yakın olması için n'nin "yeterince büyük" olduğunu varsaymak gelenekseldir . ${\ Displaystyle {\hat {\beta }}}$${\displaystyle {\hat {\sigma }}^{2}}$

Bu model, varsayımlar altında, en az kareli tahmincisi olduğunu gösterebilir p olan tutarlı (olduğunu olasılık yakınsamaktadır için P : ve asimptotik normal) ^[geçirmez]${\ Displaystyle {\hat {\beta }}}$

${\displaystyle ({\hat {\beta }}-\beta )\ {\xrightarrow {d}}\ {\mathcal {N}}{\big (}0,\;\sigma ^{2}Q_{xx) }^{-1}{\büyük )},}$

nerede ${\displaystyle Q_{xx}=X^{T}X.}$

Aralıklar

Bu asimptotik dağılımı kullanarak , vektörün j -inci bileşeni için yaklaşık iki taraflı güven aralıkları şu şekilde oluşturulabilir: ${\ Displaystyle {\hat {\beta }}}$

${\displaystyle \beta _{j}\in {\bigg [}\ {\hat {\beta }}_{j}\pm q_{1-{\frac {\alpha }{2}}}^{{ \mathcal {N}}(0,1)}\!{\sqrt {{\hat {\sigma }}^{2}\left[Q_{xx}^{-1}\sağ]_{jj}} }\ {\büyük ]}}$   de 1 -  α güven seviyesinde,

burada q belirtmektedir miktarsal fonksiyonunu , standart normal dağılımın ve [·] _jj olan j matris inci çapraz eleman.

Benzer şekilde, σ ² için en küçük kareler tahmincisi de tutarlı ve asimptotik olarak normaldir ( e _i'nin dördüncü momentinin mevcut olması şartıyla ) sınırlayıcı dağılımla

${\displaystyle ({\hat {\sigma }}^{2}-\sigma ^{2})\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\operatöradı { E} \sol[\varepsilon _{i}^{4}\sağ]-\sigma ^{4}\sağ).}$

Bu asimptotik dağılımlar tahmin, hipotezlerin test edilmesi, diğer tahmin edicilerin oluşturulması vb. için kullanılabilir. Örnek olarak tahmin problemini ele alalım. Regresörlerin dağılım alanı içinde bir nokta olduğunu varsayalım ve kişi bu noktada yanıt değişkeninin ne olacağını bilmek istiyor. Ortalama tepki miktar ise, tahmin edilen cevap olup . Açıkça tahmin edilen yanıt rastgele bir değişkendir, dağılımı aşağıdakilerden türetilebilir : ${\görüntüleme stili x_{0}}$${\displaystyle y_{0}=x_{0}^{\mathrm {T} }\beta }$${\displaystyle {\hat {y}}_{0}=x_{0}^{\mathrm {T} }{\hat {\beta }}}$${\ Displaystyle {\hat {\beta }}}$

${\displaystyle \left({\hat {y}}_{0}-y_{0}\right)\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\sigma) ^{2}x_{0}^{\mathrm {T} }Q_{xx}^{-1}x_{0}\sağ),}$

bu, oluşturulacak ortalama yanıt için yapı güven aralıklarına izin verir : ${\görüntüleme stili y_{0}}$

${\displaystyle y_{0}\in \sol[\ x_{0}^{\mathrm {T} }{\hat {\beta }}\pm q_{1-{\frac {\alpha }{2}} }^{{\mathcal {N}}(0,1)}\!{\sqrt {{\hat {\sigma }}^{2}x_{0}^{\mathrm {T} }Q_{xx} ^{-1}x_{0}}}\ \sağ]}$   de 1 -  α güven seviyesinde.

Hipotez testi

İki hipotez testi özellikle yaygın olarak kullanılmaktadır. Birincisi, tahmin edilen regresyon denkleminin, yanıt değişkeninin tüm değerlerinin örnek ortalamasına eşit olduğunu basitçe tahmin etmekten daha iyi olup olmadığını bilmek ister (eğer değilse, açıklayıcı gücünün olmadığı söylenir). Boş hipotez tahmini regresyon açıklayıcı bir değeri olan bir kullanılarak test edilir , F-testi . Hesaplanan F değeri, önceden seçilen anlamlılık düzeyi için kritik değerini aşacak kadar büyük bulunursa, sıfır hipotezi reddedilir ve regresyonun açıklayıcı güce sahip olduğu alternatif hipotezi kabul edilir. Aksi takdirde, açıklayıcı gücün olmadığı sıfır hipotezi kabul edilir.

İkinci olarak, ilgilenilen her açıklayıcı değişken için, tahmin edilen katsayısının sıfırdan önemli ölçüde farklı olup olmadığını, yani bu özel açıklayıcı değişkenin aslında yanıt değişkenini tahmin etmede açıklayıcı güce sahip olup olmadığını bilmek istenir. Burada boş hipotez, gerçek katsayının sıfır olmasıdır. Bu hipotez, katsayı tahmininin standart hatasına oranı olarak katsayının t-istatistiği hesaplanarak test edilir . t istatistiği önceden belirlenmiş bir değerden büyükse, sıfır hipotezi reddedilir ve değişkenin katsayısı sıfırdan önemli ölçüde farklı olan açıklayıcı güce sahip olduğu bulunur. Aksi takdirde, gerçek katsayının sıfır değerinin sıfır hipotezi kabul edilir.

Ek olarak, Chow testi , iki alt örneğin her ikisinin de aynı temel gerçek katsayı değerlerine sahip olup olmadığını test etmek için kullanılır. Her bir alt kümedeki ve birleştirilmiş veri kümesindeki regresyonların artık karelerinin toplamı, bir F-istatistiğinin hesaplanmasıyla karşılaştırılır; eğer bu kritik bir değeri aşarsa, iki altküme arasında fark olmadığına dair boş hipotez reddedilir; aksi halde kabul edilir.

Gerçek verilerle örnek

Aşağıdaki veri seti, 30-39 yaş arası Amerikalı kadınların ortalama boy ve kilolarını vermektedir (kaynak: The World Almanac and Book of Facts, 1975 ).

Yükseklik (m)	1.47	1.50	1.52	1.55	1.57	1.60	1,63	1.65	1.68	1.70	1.73	1.75	1.78	1.80	1.83
Ağırlık (kg)	52.21	53.12	54.48	55.84	57.20	58.57	59.93	61.29	63.11	64.47	66.28	68.10	69.92	72.19	74.46

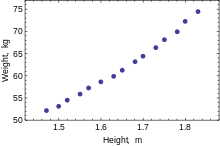
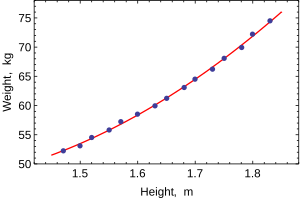
Yalnızca bir bağımlı değişken modellendiğinde, bir dağılım grafiği bağımlı değişken ile regresörler arasındaki ilişkinin biçimini ve gücünü önerecektir. Ayrıca, uygun bir regresyon modelinin yorumlanmasını karmaşıklaştırabilecek verilerin aykırı değerleri, değişen varyanslılığı ve diğer yönlerini ortaya çıkarabilir. Dağılım grafiği, ilişkinin güçlü olduğunu ve ikinci dereceden bir fonksiyon olarak tahmin edilebileceğini gösterir. OLS, HEIGHT ² regresörünü tanıtarak doğrusal olmayan ilişkileri işleyebilir . Regresyon modeli daha sonra çoklu doğrusal bir model haline gelir:

${\displaystyle w_{i}=\beta _{1}+\beta _{2}h_{i}+\beta _{3}h_{i}^{2}+\varepsilon _{i}.}$

En popüler istatistik paketlerinin çıktısı şuna benzer:

Yöntem	En küçük kareler
Bağımlı değişken	AĞIRLIK
gözlemler	15
Parametre	Değer	Std. Hata	t-istatistik	p değeri
${\görüntüleme stili \beta _{1}}$	128.8128	16.3083	7.8986	0.0000
${\displaystyle \beta _{2}}$	–143.1620	19.8332	–7.2183	0.0000
${\görüntüleme stili \beta _{3}}$	61.9603	6.0084	10.3122	0.0000
R, 2	0.9989	gerileme SE		0.2516
Ayarlanmış R 2	0.9987	Model toplamı metrekare		692.61
Log olasılığı	1.0890	Kalan toplam metrekare		0.7595
Durbin-Watson durumu.	2.1013	Toplam metrekare		693,37
Akaike kriteri	0.2548	F-istatistiği		5471.2
Schwarz kriteri	0.3964	p-değeri (F-stat)		0.0000

Bu tabloda:

• Değer sütun parametrelerin en küçük kareler tahminleri verir β _j
• Std hata sütunda, standart hatalar her katsayı tahmin:${\displaystyle {\hat {\sigma }}_{j}=\left({\hat {\sigma }}^{2}\left[Q_{xx}^{-1}\sağ]_{jj} \sağ)^{\frac {1}{2}}}$
• T-istatistiği ve p-değeri sütunları katsayılarının bir sıfıra eşit olabilir olup olmadığını test edilir. T , sadece şu şekilde hesaplanır -statistic . Hatalar ε normal bir dağılımı takip ediyorsa, t bir Student-t dağılımını takip eder. Daha zayıf koşullar altında, t asimptotik olarak normaldir. Büyük t değerleri , boş hipotezin reddedilebileceğini ve karşılık gelen katsayının sıfır olmadığını gösterir. İkinci sütun, p- değeri , hipotez testinin sonuçlarını anlamlılık düzeyi olarak ifade eder . Geleneksel olarak, 0,05'ten küçük p -değerleri, popülasyon katsayısının sıfır olmadığına dair kanıt olarak alınır.${\displaystyle t={\hat {\beta }}_{j}/{\hat {\sigma }}_{j}}$
• R-kare , regresyonun uyum iyiliğini gösteren belirleme katsayısıdır . Bu istatistik, eğer uyum mükemmelse bire, X regresörlerinin herhangi bir açıklayıcı gücü olmadığında ise sıfıra eşit olacaktır . Bu, R-kare popülasyonunun taraflı bir tahminidir ve alakasız olsalar bile ilave regresörler eklenirse asla azalmayacaktır.
• Düzeltilmiş R-kare , regresyonun açıklayıcı gücüne katkıda bulunmayan fazla sayıda regresör için ceza vermek üzere tasarlanmış, biraz değiştirilmiş bir versiyonudur . Bu istatistik her zaman 'den küçüktür , yeni regresörler eklendikçe azalabilir ve hatta uygun olmayan modeller için negatif olabilir:${\ Displaystyle R^{2}}$${\ Displaystyle R^{2}}$

${\displaystyle {\overline {R}}^{2}=1-{\frac {n-1}{np}}(1-R^{2})}$

• Log-olasılığı , hataların normal dağılımı takip ettiği varsayımı altında hesaplanır. Varsayım çok makul olmasa da, bu istatistik yine de LR testlerinin yürütülmesinde kullanımını bulabilir.
• Durbin-Watson istatistiği , artıklar arasında herhangi bir seri korelasyon kanıtı olup olmadığını test eder. Genel bir kural olarak, 2'den küçük değer, pozitif korelasyonun bir kanıtı olacaktır.
• Akaike bilgi kriteri ve Schwarz kriter hem modeli seçimi için kullanılmaktadır. Genellikle iki alternatif modeli karşılaştırırken, bu kriterlerden birinin daha küçük değerleri daha iyi bir modeli gösterir.
• Standart regresyon hatası, hata teriminin standart hatası olan σ tahminidir .
• Toplam karelerinin toplamı , kare model toplamı ve rezidüel kareler toplamı regresyon ile açıklanabilir nasıl numunede ilk varyasyonun çok bize.
• F-istatistiği , tüm katsayıların (kesme hariç) sıfıra eşit olduğu hipotezini test etmeye çalışır. Bu istatistik, sıfır hipotezi ve normallik varsayımı altında F ( p–1 , n–p ) dağılımına sahiptir ve p değeri , hipotezin gerçekten doğru olma olasılığını gösterir. Hatalar normal olmadığında bu istatistiğin geçersiz hale geldiğini ve Wald testi veya LR testi gibi diğer testlerin kullanılması gerektiğini unutmayın.

Olağan en küçük kareler analizi, genellikle, verilerin varsayılan model biçiminden sapmalarını tespit etmek için tasarlanmış tanılama grafiklerinin kullanımını içerir. Bunlar, yaygın tanılama grafiklerinden bazılarıdır:

• Modeldeki açıklayıcı değişkenlere karşı artıklar. Bu değişkenler arasındaki doğrusal olmayan bir ilişki, koşullu ortalama fonksiyonunun doğrusallığının geçerli olmayabileceğini gösterir. Açıklayıcı değişkenlerin farklı seviyeleri için artıklardaki farklı değişkenlik seviyeleri, olası değişen varyansı düşündürür.
• Modelde olmayan açıklayıcı değişkenlere karşı artıklar. Kalıntıların bu değişkenlerle herhangi bir ilişkisi, bu değişkenlerin modele dahil edilmesi için dikkate alınmasını önerir.
• Takılan değerlere karşı artıklar, .${\görüntüleme stili {\şapka {y}}}$
• Önceki kalıntıya karşı kalıntılar. Bu çizim, artıklardaki seri korelasyonları tanımlayabilir.

Regresyon modellerini kullanarak istatistiksel çıkarım yaparken önemli bir husus, verilerin nasıl örneklendiğidir. Bu örnekte, veriler tek tek kadınlara ilişkin ölçümler yerine ortalamalardır. Modelin uyumu çok iyidir, ancak bu, bir kadının ağırlığının yalnızca boyuna dayalı olarak yüksek doğrulukla tahmin edilebileceği anlamına gelmez.

Yuvarlama duyarlılığı

Bu örnek ayrıca, bu hesaplamalarla belirlenen katsayıların, verilerin nasıl hazırlandığına duyarlı olduğunu da göstermektedir. Yükseklikler başlangıçta en yakın inç'e yuvarlatılmış olarak verilmiş ve dönüştürülmüş ve en yakın santimetreye yuvarlanmıştır. Dönüştürme faktörü bir inç ila 2,54 cm olduğundan, bu tam bir dönüşüm değildir . Orijinal inç, Round(x/0.0254) ile geri alınabilir ve daha sonra yuvarlamadan tekrar metriğe dönüştürülebilir. Bu yapılırsa sonuçlar şöyle olur:

	Sabit	Boy uzunluğu	Yükseklik 2
Yuvarlama ile metriğe dönüştürülür.	128.8128	-143.162	61.96033
Yuvarlama yapılmadan metriğe dönüştürülür.	119.0205	-131.5076	58.5046

5' 6" (1.6764 m) bir kadının ağırlığını tahmin etmek için bu denklemlerden herhangi birinin kullanılması, benzer değerler verir: yuvarlatılmış 62.94 kg ve yuvarlamadan 62.98 kg. Dolayısıyla verilerdeki görünüşte küçük bir varyasyon katsayılar üzerinde gerçek bir etkiye sahiptir. ancak denklemin sonuçları üzerinde küçük bir etkisi vardır.

Bu, veri aralığının ortasında zararsız görünse de, uç noktalarda veya takılan modelin veri aralığının dışına yansıtmak için kullanıldığı ( ekstrapolasyon ) durumda önemli hale gelebilir .

Bu, yaygın bir hatayı vurgular: bu örnek, doğası gereği bağımsız değişkendeki (bu durumda yükseklik) hataların sıfır veya en azından ihmal edilebilir olmasını gerektiren OLS'nin kötüye kullanılmasıdır. En yakın inç'e ilk yuvarlama artı herhangi bir gerçek ölçüm hatası, sonlu ve ihmal edilemez bir hata oluşturur. Sonuç olarak, uydurulan parametreler tahmin edildikleri en iyi tahminler değildir. Tamamen sahte olmasa da, tahmindeki hata, x ve y hatalarının göreceli boyutuna bağlı olacaktır .

Daha az gerçek veri içeren başka bir örnek

Sorun bildirimi

Kutupsal taban koordinatlarında iki cisim yörüngesinin denklemini bulmak için en küçük kareler mekanizmasını kullanabiliriz. Tipik olarak kullanılan denklem , nesnenin gövdelerden birinden ne kadar uzakta olduğunun yarıçapının nerede olduğudur. Denklemde parametreler ve yörüngenin yolunu belirlemek için kullanılır. Aşağıdaki verileri ölçtük. ${\displaystyle r(\theta )={\frac {p}{1-e\cos(\theta )}}}$${\görüntüleme stili r(\teta)}$${\görüntüleme stili p}$${\görüntüleme stili e}$

${\görüntüleme stili\teta }$ (derece olarak)	43	45	52	93	108	116
${\görüntüleme stili r(\teta)}$	4.7126	4.5542	4.0419	2.2187	1.8910	1.7599

Verilen veriler için ve en küçük kareler yaklaşımını bulmamız gerekiyor . ${\görüntüleme stili e}$${\görüntüleme stili p}$

Çözüm

İlk önce e ve p'yi doğrusal bir biçimde temsil etmemiz gerekiyor. O halde denklemi şu şekilde yeniden yazacağız . Şimdi bu formu gözlemsel verilerimizi şu şekilde temsil etmek için kullanabiliriz: ${\görüntüleme stili r(\teta)}$${\displaystyle {\frac {1}{r(\theta )}}={\frac {1}{p}}-{\frac {e}{p}}\cos(\theta )}$

${\displaystyle A^{T}A{\binom {x}{y}}=A^{T}b}$burada olduğu ve olduğu ve katsayısı; birinci kolon ile inşa edilir ve katsayısı olan ikinci bir kolon ve bir karşılık gelen değerleri So ve${\görüntüleme stili x}$${\displaystyle {\frac {1}{p}}}$${\görüntüleme stili y}$${\displaystyle {\frac {e}{p}}}$${\görüntüleme stili A}$${\displaystyle {\frac {1}{p}}}$${\displaystyle {\frac {e}{p}}}$${\görüntüleme stili b}$${\displaystyle {\frac {1}{r(\theta )}}}$${\displaystyle A={\begin{bmatrix}1&-0.731354\\1&-0.707107\\1&-0.615661\\1&\ 0.052336\\1&0.39017\\1&0.438371\end{bmatrix}}}$${\displaystyle b={\begin{bmatrix}0.21220\\0.21958\\0.24741\\0.45071\\0.52883\\0.56820\end{bmatrix}}.}$

Çözerken elde ederiz ${\displaystyle {\binom {x}{y}}={\binom {0.43478}{0.30435}}}$

yani ve${\displaystyle p={\frac {1}{x}}=2.3000}$${\displaystyle e=p\cdot y=0.70001}$

Ayrıca bakınız

• Bayes en küçük kareler
• Fama-MacBeth regresyonu
• Doğrusal olmayan en küçük kareler
• Doğrusal en küçük kareler için sayısal yöntemler
• Doğrusal olmayan sistem tanımlama

Referanslar

daha fazla okuma

• Dougherty, Christopher (2002). Ekonometriye Giriş (2. baskı). New York: Oxford University Press. s. 48–113. ISBN'si 0-19-877643-8.
• Gujarati, Damodar N. ; Porter, Şafak C. (2009). Temel Ekonomi (Beşinci baskı). Boston: McGraw-Hill Irwin. s. 55–96. ISBN'si 978-0-07-337577-9.
• Heij, Christian; Boer, Paul; Franses, Philip H.; Kloek, Teun; van Dijk, Herman K. (2004). İşletme ve Ekonomi Uygulamaları ile Ekonometrik Yöntemler (1. baskı). Oxford: Oxford University Press. s. 76–115. ISBN'si 978-0-19-926801-6.
• Hill, R. Carter; Griffiths, William E.; Lim, Guay C. (2008). Ekonometrinin İlkeleri (3. baskı). Hoboken, NJ: John Wiley & Sons. s. 8–47. ISBN'si 978-0-471-72360-8.
• Wooldridge, Jeffrey (2008). "Basit Regresyon Modeli" . Giriş Ekonometrisi: Modern Bir Yaklaşım (4. baskı). Mason, OH: Cengage Learning. s. 22–67. ISBN'si 978-0-324-58162-1.