Tek boyutlu normal dağılımın daha yüksek boyutlara genelleştirilmesi
Gelen Olasılık teorisi ve istatistik , çok değişkenli normal dağılım , çok değişkenli normal dağılım veya ortak normal dağılım tek boyutlu (bir genellemedir tek değişkenli ) normal dağılım daha yüksek boyutlarda . Bir tanım olmasıdır rasgele vektör olduğu söylenir k her halinde -variate normal dağılım lineer birleşimi olan bir k bileşenleri bir tek değişkenli normal bir dağılıma sahiptir. Önemi esas olarak çok değişkenli merkezi limit teoreminden kaynaklanmaktadır . Çok değişkenli normal dağılım genellikle, en azından yaklaşık olarak, her biri ortalama bir değer etrafında kümelenen (muhtemelen) herhangi bir korelasyonlu gerçek değerli rastgele değişken kümesini tanımlamak için kullanılır .
Tanımlar
Notasyon ve parametreleştirme
Bir k boyutlu rastgele vektörün çok değişkenli normal dağılımı aşağıdaki gösterimle yazılabilir:


veya açıkça bilinmektedir yapmak X'in ise k , -boyutlu

ile k boyutlu ortalama vektörü
![{\displaystyle {\boldsymbol {\mu }}=\operatöradı {E} [\mathbf {X} ]=(\operatöradı {E} [X_{1}],\operatöradı {E} [X_{2}], \ldots ,\operatöradı {E} [X_{k}])^{\textbf {T}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e69e434645f47377bc8766624255c8026adf7964)
ve kovaryans matrisi
![{\displaystyle \Sigma _{i,j}=\operatöradı {E} [(X_{i}-\mu _{i})(X_{j}-\mu _{j})]=\operatöradı {Cov } [X_{i},X_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c970083f8469366521881996464f23d376b7c40b)
öyle ki ters kovaryans matrisinin denir hassas ile gösterilen, bir matris .


Standart normal rastgele vektör
Gerçek bir rastgele vektör , eğer tüm bileşenleri bağımsızsa ve her biri sıfır ortalamalı birim varyans normal dağılımlı rastgele değişkense, yani tümü için ise, standart normal rastgele vektör olarak adlandırılır .




Merkezlenmiş normal rastgele vektör
Gerçek rasgele vektör bir adlandırılır merkezli normal rasgele vektör deterministik mevcutsa matris gibi aynı dağılımına sahip burada bir standart normal rasgele vektör bileşenleri.







Normal rastgele vektör
Gerçek rasgele vektör denen normal bir rasgele vektör rasgele mevcutsa -vector standart normal rasgele vektör, bir olduğunu -vector ve matris , öyle ki .








Resmi olarak:

İşte kovaryans matrisi olduğunu .

Olarak dejenere kovaryans matrisidir durumda tekil , karşılık gelen dağıtım bir yoğunluğa sahiptir; bakınız aşağıdaki bölümü ayrıntılar için. Bu durum istatistiklerde sıklıkla karşımıza çıkmaktadır ; Örneğin, bir vektörün dağılımında artıkları içinde , en küçük kareler regresyon. Genel olarak değil , bağımsız; matrisin bağımsız Gauss değişkenleri koleksiyonuna uygulanmasının sonucu olarak görülebilirler .



eşdeğer tanımlar
Aşağıdaki tanımlar, yukarıda verilen tanıma eşdeğerdir. Rastgele bir vektör , aşağıdaki eşdeğer koşullardan birini sağlıyorsa çok değişkenli normal dağılıma sahiptir.

- Bileşenlerinin her doğrusal kombinasyonu normal olarak dağıtılır . Yani, herhangi bir sabit vektör için , rastgele değişken tek değişkenli normal dağılıma sahiptir, burada sıfır varyanslı tek değişkenli normal dağılım, ortalaması üzerinde bir nokta kütledir.



- Bir vardır k -vector ve simetrik bir, pozitif yarı kesin matris , bu şekilde karakteristik fonksiyonu arasında IS





Küresel normal dağılım, bileşenlerin herhangi bir ortogonal koordinat sisteminde bağımsız olduğu benzersiz dağılım olarak karakterize edilebilir.
Yoğunluk fonksiyonu
dejenere olmayan durum
Çok değişkenli normal dağılım simetrik olduğunda "dejenere" olduğu söylenir kovaryans matrisi olan pozitif tanımlı . Bu durumda dağılımın yoğunluğu vardır

nerede bir gerçek k boyutlu sütun vektörü ve bir belirleyici ait olarak da bilinen, genelleştirilmiş varyans . Yukarıdaki denklem bir matris ise (yani tek bir gerçek sayı) tek değişkenli normal dağılıma indirgenir .





Karmaşık normal dağılımın dairesel simetrik versiyonu biraz farklı bir forma sahiptir.
Her bir eş-yoğunluk yeri - k -boyutlu uzayda her biri aynı yoğunluk değerini veren noktaların yeri - bir elips veya onun daha yüksek boyutlu genellemesidir; dolayısıyla çok değişkenli normal, eliptik dağılımların özel bir halidir .
Miktar , test noktasının ortalamadan uzaklığını temsil eden Mahalanobis mesafesi olarak bilinir . Dağılımın tek değişkenli normal dağılıma düştüğü ve Mahalanobis mesafesinin standart puanın mutlak değerine düştüğü durumda unutmayın . Ayrıca bkz Aralığı altında.




iki değişkenli durum
2 boyutlu tekil olmayan durumda ( ), bir vektörün olasılık yoğunluk fonksiyonu şudur:

![{\görüntüleme stili {\metin{[XY]′}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24925a0dd360004248b2a1de70e2b0bcf3fcf687)
![{\displaystyle f(x,y)={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}}\exp \left(-{\frac {1}{2(1-\rho ^{2})}}\left[\left({\frac {x-\mu _{X}}{\sigma _{X}) }}\sağ)^{2}-2\rho \left({\frac {x-\mu _{X}}{\sigma _{X}}}\sağ)\sol({\frac {y- \mu _{Y}}{\sigma _{Y}}}\sağ)+\sol({\frac {y-\mu _{Y}}{\sigma _{Y}}}\sağ)^{ 2}\sağ]\sağ)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c616921276f29c0c0cd5383fd81045939f8f6e82)
nerede olduğunu korelasyon arasındaki ve nerede ve . Bu durumda,






Doğrulamak için yeterli olduğu iki değişkenli durumda, normallik değişkenli yeniden ilk eş durumu az kısıtlayıcı yapılabilir sayılabilir birçok ayrı doğrusal kombinasyonlarını ve vektör sonucuna amacıyla normal normal bir değişkenli bir.


![{\görüntüleme stili {\metin{[XY]′}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24925a0dd360004248b2a1de70e2b0bcf3fcf687)
-düzleminde çizilen iki değişkenli eş yoğunluklu lokuslar , ana eksenleri kovaryans matrisinin özvektörleri tarafından tanımlanan elipslerdir ( elipsin büyük ve küçük yarı çapları , sıralı özdeğerlerin kareköküne eşittir).


Korelasyon parametresinin mutlak değeri arttıkça, bu lokuslar aşağıdaki satıra doğru sıkıştırılır:


Bu ifade, Bunun nedeni (sgn olan İşaret fonksiyonu yerine) olduğu en iyi lineer yansız tahmin ait bir değer verilir .




dejenere vaka
Kovaryans matrisi tam sıra değilse, çok değişkenli normal dağılım dejeneredir ve yoğunluğu yoktur. Daha kesin olarak, k -boyutlu Lebesgue ölçüsüne göre bir yoğunluğa sahip değildir (ki bu, hesap düzeyinde olasılık derslerinde kabul edilen olağan ölçüdür). Yalnızca bir ölçüye göre dağılımları mutlak olarak sürekli olan rastgele vektörlerin yoğunlukları olduğu söylenir (bu ölçüye göre). Yoğunluklar hakkında konuşmak, ancak ölçü-teorik komplikasyonlarla uğraşmaktan kaçınmak için, dikkati koordinatların bir alt kümesine sınırlamak , bu alt küme için kovaryans matrisi pozitif tanımlı olacak şekilde daha basit olabilir ; o zaman diğer koordinatlar , bu seçilmiş koordinatların afin bir fonksiyonu olarak düşünülebilir .



Tekil durumlarda yoğunluklar hakkında anlamlı bir şekilde konuşmak için, farklı bir temel ölçü seçmeliyiz. Parçalanma teoremini kullanarak, Lebesgue ölçüsünün , Gauss dağılımının desteklendiği yerin -boyutlu afin alt uzayına , yani . Bu ölçü ile ilgili olarak dağılım, aşağıdaki motifin yoğunluğuna sahiptir:




nerede olduğunu genelleştirilmiş ters ve det * olan sözde belirleyici .

Kümülatif dağılım fonksiyonu
Boyut 1'deki kümülatif dağılım fonksiyonu (cdf) kavramı , dikdörtgen ve elipsoidal bölgelere dayalı olarak çok boyutlu duruma iki şekilde genişletilebilir.
İlk yol, rastgele bir vektörün cdf'sini , tüm bileşenlerinin vektördeki karşılık gelen değerlerden küçük veya eşit olma olasılığı olarak tanımlamaktır :





için kapalı bir form olmamasına rağmen , onu sayısal olarak tahmin eden bir takım algoritmalar vardır .

Diğer bir yol, cdf'yi , standart sapmanın doğrudan bir genellemesi olan, Gauss'tan Mahalanobis mesafesi ile belirlenen bir örneğin elipsoidin içinde yer alma olasılığı olarak tanımlamaktır . Bu fonksiyonun değerlerini hesaplamak için aşağıdaki gibi kapalı analitik formüller mevcuttur.


Aralık
Aralığı çok değişkenli normal dağılım için, bu vektörler aşağıdakilerden oluşan bir bölge elde edilir x tatmin

Burada a, boyutlu vektör, bilinen boyutlu ortalama vektörü, bir bilinen kovaryans matrisi ve bir miktarsal fonksiyon olasılık arasında ki-kare dağılımı ile serbestlik derecesi. Zaman ifade elips ve chi-square dağıtım basitleştirir iç tanımlayan üstel dağılımı iki eşit ortalama ile (oran yarısına eşit).









Tamamlayıcı kümülatif dağılım işlevi (kuyruk dağılımı)
Tamamlayıcı kümülatif dağılım fonksiyonu (CCDF) ya da kuyruk dağılımı
olarak tanımlanır . olduğunda , ccdf, bağımlı Gauss değişkenlerinin maksimumu bir olasılık olarak yazılabilir:



ccdf'yi hesaplamak için basit bir kapalı formül bulunmamakla birlikte, maksimum bağımlı Gauss değişkenleri Monte Carlo yöntemiyle doğru bir şekilde tahmin edilebilir .
Özellikler
Farklı alanlarda olasılık
Gauss diskriminant analizini kullanan Bayes sınıflandırması/karar teorisi ile ilgili olan (burada bir matris, bir vektördür ve bir skalerdir) ile tanımlanan ikinci dereceden bir alanda çok değişkenli normalin olasılık içeriği , genelleştirilmiş ki- kare dağılım . Tarafından tanımlanan herhangi bir genel etki alanı içindeki olasılık içeriği (burada genel bir işlevdir) sayısal ışın izleme yöntemi ( Matlab kodu ) kullanılarak hesaplanabilir .






Daha yüksek anlar
K inci dereceden anlar ait x tarafından verilmektedir
![{\displaystyle \mu _{1,\ldots ,N}(\mathbf {x} )\ {\stackrel {\mathrm {def} }{=}}\ \mu _{r_{1},\ldots ,r_ {N}}(\mathbf {x} )\ {\stackrel {\mathrm {def} }{=}}\operatöradı {E} \left[\prod _{j=1}^{N}X_{j} ^{r_{j}}\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68bafb23658afe2f4246d5f27781aac7eeacbaa7)
burada r 1 + r 2 + ⋯ + r N = k .
K inci dereceden merkez anlar olarak aşağıda olan
- Eğer k , garip μ 1, ..., N ( x - μ = 0) .
- Eğer k bile ile k = 2 X , daha sonra

toplam setinin tüm tahsisler üzerinden alınır burada içine λ (sırasız) çiftleri. Yani, bir k th (= 2 λ = 6) merkezi moment için, λ = 3 kovaryansın ürünleri toplanır (beklenen değer μ , cimriliğin yararına 0 olarak alınır):

![{\displaystyle {\begin{hizalanmış}&\operatöradı {E} [X_{1}X_{2}X_{3}X_{4}X_{5}X_{6}]\\[8pt]={}& \operatöradı {E} [X_{1}X_{2}]\operatöradı {E} [X_{3}X_{4}]\operatöradı {E} [X_{5}X_{6}]+\operatöradı {E } [X_{1}X_{2}]\operatöradı {E} [X_{3}X_{5}]\operatöradı {E} [X_{4}X_{6}]+\operatöradı {E} [X_{ 1}X_{2}]\operatöradı {E} [X_{3}X_{6}]\operatöradı {E} [X_{4}X_{5}]\\[4pt]&{}+\operatöradı {E } [X_{1}X_{3}]\operatöradı {[} X_{2}X_{4}]\operatöradı {E} [X_{5}X_{6}]+\operatöradı {E} [X_{1 }X_{3}]\operatöradı {E} [X_{2}X_{5}]\operatöradı {E} [X_{4}X_{6}]+\operatöradı {E} [X_{1}X_{3 }]\operatöradı {E} [X_{2}X_{6}]\operatöradı {E} [X_{4}X_{5}]\\[4pt]&{}+\operatöradı {E} [X_{1 }X_{4}]\operatöradı {E} [X_{2}X_{3}]\operatöradı {E} [X_{5}X_{6}]+\operatöradı {E} [X_{1}X_{4 }]\operatöradı {E} [X_{2}X_{5}]\operatöradı {E} [X_{3}X_{6}]+\operatöradı {E} [X_{1}X_{4}]\operatöradı {E} [X_{2}X_{6}]\operatöradı {E} [X_{3}X_{5}]\\[4pt]&{}+\operatöradı {E} [X_{1}X_{5 }]\operatöradı {E} [X_{2}X_{3} ]\operatöradı {E} [X_{4}X_{6}]+\operatöradı {E} [X_{1}X_{5}]\operatöradı {E} [X_{2}X_{4}]\operatöradı { E} [X_{3}X_{6}]+\operatöradı {E} [X_{1}X_{5}]\operatöradı {E} [X_{2}X_{6}]\operatöradı {E} [X_ {3}X_{4}]\\[4pt]&{}+\operatöradı {E} [X_{1}X_{6}]\operatöradı {E} [X_{2}X_{3}]\operatöradı { E} [X_{4}X_{5}]+\operatöradı {E} [X_{1}X_{6}]\operatöradı {E} [X_{2}X_{4}]\operatöradı {E} [X_ {3}X_{5}]+\operatöradı {E} [X_{1}X_{6}]\operatöradı {E} [X_{2}X_{5}]\operatöradı {E} [X_{3}X_ {4}].\end{hizalanmış}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec24a2d6baf16b88926e5e83fb8e4005c5a2541a)
Bu , her biri λ (bu durumda 3) kovaryanslarının ürünü olan toplamda (yukarıdaki durumda 15) terimleri verir . Dördüncü dereceden momentler (dört değişken) için üç terim vardır. Altıncı dereceden anlar için 3 × 5 = 15 terim vardır ve sekizinci dereceden anlar için 3 × 5 × 7 = 105 terim vardır.

Daha sonra kovaryanslar, listenin terimlerinin r 1 birler, sonra r 2 ikiler, vb.'den oluşan listenin karşılık gelen terimleriyle değiştirilmesiyle belirlenir . Bunu göstermek için aşağıdaki 4. mertebe merkezi moment durumunu inceleyin:
![{\displaystyle [1,\ldots ,2\lambda ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a605bf32a38577fe9df1bc5715a4a3cac5869832)
![{\displaystyle {\begin{hizalanmış}\operatöradı {E} \sol[X_{i}^{4}\sağ]&=3\sigma _{ii}^{2}\\[4pt]\operatöradı {E } \left[X_{i}^{3}X_{j}\sağ]&=3\sigma _{ii}\sigma _{ij}\\[4pt]\operatöradı {E} \left[X_{i }^{2}X_{j}^{2}\sağ]&=\sigma _{ii}\sigma _{jj}+2\sigma _{ij}^{2}\\[4pt]\operatöradı { E} \left[X_{i}^{2}X_{j}X_{k}\sağ]&=\sigma _{ii}\sigma _{jk}+2\sigma _{ij}\sigma _{ ik}\\[4pt]\operatöradı {E} \left[X_{i}X_{j}X_{k}X_{n}\right]&=\sigma _{ij}\sigma _{kn}+\ sigma _{ik}\sigma _{jn}+\sigma _{in}\sigma _{jk}.\end{hizalı}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e08f5bc180e3f1f4379c1026100e833ea85de97)
X i ve X j'nin kovaryansı nerede . Yukarıdaki yöntem, bir birinci buluntular bir genel olgu ile k th an k farklı X değişkenleri, bu konuyla ilgili olarak, ve daha sonra bir basitleştirir. Örneğin, için biri X i = X j sağlar ve biri .

![{\displaystyle E\sol[X_{i}X_{j}X_{k}X_{n}\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4bbbf2becaf15b246898e928a37e7d0ab6f93a)
![{\displaystyle \operatöradı {E} [X_{i}^{2}X_{k}X_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7bc1920d0e524aa567ca471bdb54dcf7ef7e673)

Normal bir vektörün işlevleri
Bir ikinci dereceden bir şekilde normal bir vektör , ( bir matris, bir vektördür ve skalar olan), a, genelleştirilmiş ki-kare değişkeni.





Eğer normal vektörü genel bir skaler değerli bir fonksiyondur, onun olasılık yoğunluk fonksiyonu , kümülatif dağılım fonksiyonu ve ters kümülatif dağılım fonksiyonu ışın izleme (sayısal yöntemle hesaplanabilmektedir Matlab kodu ).

olasılık fonksiyonu
Ortalama ve kovaryans matrisi biliniyorsa, gözlemlenen bir vektörün log olasılığı basitçe olasılık yoğunluk fonksiyonunun logu olur :

-
![{\displaystyle \ln L({\boldsymbol {x}})=-{\frac {1}{2}}\left[\ln(|{\boldsymbol {\Sigma }}}|\,)+({\ boldsymbol {x}}-{\boldsymbol {\mu }})'{\boldsymbol {\Sigma }}^{-1}({\boldsymbol {x}}-{\boldsymbol {\mu }})+k\ ln(2\pi )\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ad05643016bbf6ac76a826320bea00704b50982) ,
,
Karmaşık sayıların bir vektörü olan
merkezi olmayan karmaşık durumun dairesel simetrik versiyonu,

yani eşlenik devrik ( ile gösterilir ) normal devrik ( ile gösterilir ) değiştirilir . Bu, gerçek durumdan biraz farklıdır, çünkü karmaşık normal dağılımın dairesel simetrik versiyonu , normalleştirme sabiti için biraz farklı bir forma sahiptir .


Benzer bir gösterim, çoklu doğrusal regresyon için kullanılır .
Normal bir vektörün log olasılığı, normal vektörün ikinci dereceden bir formu olduğundan, genelleştirilmiş bir ki-kare değişkeni olarak dağıtılır .
diferansiyel entropi
Diferansiyel entropi değişkenli normal dağılım olduğu

burada çubuklar matris determinantını ve k vektör uzayının boyutluluğunu gösterir.
Kullback-Leibler ayrışması
Kullback-Leibler ıraksama gelen için tekil olmayan matrisler Σ için, 1 ve Σ 0 olduğu:



vektör uzayının boyutu nerede .

Logaritma baz alınmalıdır e logaritma aşağıdaki iki terim baz- kendileri çünkü E yoğunluk fonksiyonunun ya faktörler ya da başka şekilde, doğal olarak ortaya çıkan ifade logaritma. Bu nedenle denklem, nats cinsinden ölçülen bir sonuç verir . Yukarıdaki ifadenin tamamını log e 2'ye bölmek, sapmayı bit olarak verir .
ne zaman ,


Karşılıklı bilgi
Karşılıklı bilgi Bir dağılımın özel bir durumdur Kullback-Leibler sapma olduğu tam değişkenli dağılım ve 1 boyutlu marjinal dağılımları ürünüdür. Arasında gösterimde Kullback-Leibler sapma bölümünün bu makalenin, bir olan köşegen matris diyagonal girişleriyle ve . Karşılıklı bilgi için elde edilen formül:






burada bir ilinti matrisi inşa .


İki değişkenli durumda karşılıklı bilgi için ifade şöyledir:

ortak normallik
Normal dağılımlı ve bağımsız
Eğer ve normal dağılmışlarsa ve bağımsızlarsa , bu onların "ortak olarak normal dağıldığı" anlamına gelir, yani çiftin çok değişkenli normal dağılıma sahip olması gerekir. Bununla birlikte, ortaklaşa normal olarak dağıtılan bir çift değişkenin bağımsız olması gerekmez (sadece korelasyonsuzsa böyle olur, ).




Normal olarak dağıtılan iki rastgele değişkenin birlikte iki değişkenli normal olması gerekmez
İki rastgele değişkenin ve her ikisinin de normal dağılıma sahip olması, çiftin ortak normal dağılıma sahip olduğu anlamına gelmez . Basit bir örnek, X'in beklenen değeri 0 ve varyansı 1 olan normal bir dağılıma sahip olduğu ve if ve if , nerede . İkiden fazla rastgele değişken için benzer karşı örnekler vardır. Genel olarak, bir karışım modelini toplarlar .








Korelasyonlar ve bağımsızlık
Genel olarak, rastgele değişkenler korelasyonsuz olabilir ancak istatistiksel olarak bağımlı olabilir. Fakat eğer rastgele bir vektör çok değişkenli normal dağılıma sahipse, o zaman ilişkisiz iki veya daha fazla bileşeni bağımsızdır . Bu, ikili olarak bağımsız olan bileşenlerinin herhangi iki veya daha fazlasının bağımsız olduğu anlamına gelir . Hemen üstünde belirttiğin gibi, öyle değil (iki rasgele değişkenler olduğu doğru ayrı ayrı , marjinal) normalde dağıtılmış ve ilişkisiz bağımsızdır.
koşullu dağılımlar
Eğer N boyutlu X aşağıdaki gibi bölümlenmiş

ve buna göre μ ve Σ aşağıdaki gibi bölünür


o zaman x 2 = a üzerinde koşullu x 1 dağılımı çok değişkenli normaldir ( x 1 | x 2 = a ) ~ N ( μ , Σ ) burada

ve kovaryans matrisi

Bu matristir Schur tamamlayıcı arasında Σ 22 yılında Σ . Bu, koşullu kovaryans matrisini hesaplamak için, kişinin genel kovaryans matrisini tersine çevirmesi, koşullandırılan değişkenlere karşılık gelen satırları ve sütunları düşürmesi ve ardından koşullu kovaryans matrisini elde etmek için geri çevirmesi anlamına gelir. İşte olan genelleştirilmiş ters arasında .


Not bilerek bu x 2 = Bir değiştiren varyans, yeni varyans spesifik değerine bağlı değildir ama bir ; belki daha şaşırtıcı bir şekilde, ortalama şu şekilde değiştirilir ; değerini bilmeden durumuyla bu karşılaştırma bir durumda hangi, x 1 dağılıma sahip olacaktır
.


Bu sonucu kanıtlamak için elde edilen ilginç bir gerçek, rastgele vektörlerin ve bağımsız olmalarıdır.


Matris Σ 12 Σ 22 -1 matris olarak bilinen regresyon katsayıları.
iki değişkenli durum
İki değişkenli durumda burada X bölünür ve , koşullu dağılımı verilen IS





nerede olduğunu korelasyon katsayısı arasındaki ve .



İki değişkenli koşullu beklenti
Genel durumda

X'in koşullu beklenen 1 X verilir 2 olduğu:

İspat: Yukarıdaki koşullu dağılımın beklentisi alınarak sonuç elde edilir .

Birim varyanslı ortalanmış durumda

Koşullu beklenti X 1 verilen x 2 olduğu

ve koşullu varyans

dolayısıyla koşullu varyans x 2'ye bağlı değildir .
Koşullu beklenti X 1 verilen X- 2 den daha büyük / küçük z olduğu:


buradaki son orana ters Mills oranı denir .
Kanıt: Son iki sonuç, sonuç kullanılarak elde edilir , böylece

-
 ve sonra kesilmiş bir normal dağılım beklentisinin özelliklerini kullanarak .
ve sonra kesilmiş bir normal dağılım beklentisinin özelliklerini kullanarak .
marjinal dağılımlar
Çok değişkenli normal rastgele değişkenlerin bir alt kümesi üzerinde marjinal dağılımı elde etmek için , ortalama vektör ve kovaryans matrisinden alakasız değişkenlerin (marjinalize edilmek istenen değişkenler) çıkarılması yeterlidir. Bunun kanıtı, çok değişkenli normal dağılımların ve lineer cebirin tanımlarından gelir.
Örnek
Let X = [ X 1 , x 2 , X- 3 ] , ortalama vektör ile olmak değişkenli normal rastgele değişkenler μ [= μ 1 , μ 2 , μ 3 ] ve kovaryans matrisi Σ (değişkenli normal dağılımlar için standart parametreleriyle). O halde X' = [ X 1 , X 3 ] ' ün ortak dağılımı μ′ = [ μ 1 , μ 3 ] ortalama vektörü ve kovaryans matrisi
ile çok değişkenli normaldir .

afin dönüşüm
Eğer Y = C + BX bir bir benzeşik transformasyon ve burada C bir olan sabitler vektörü ve B sabittir matris, daha sonra , Y beklenen değer ile bir çok değişkenli normal dağılımına sahip c + Bμ varyans BΣB T , yani . Özellikle, herhangi bir alt-kümesi , X i de çok değişkenli normal bir marjinal dağılımına sahiptir. Bunu görmek için aşağıdaki örneği göz önünde bulundurun: ( X 1 , X 2 , X 4 ) T alt kümesini çıkarmak için şunu kullanın:





hangi istenen öğeleri doğrudan çıkarır.
Başka bir sonuç dağılımı yani Z = b · X , B gibi elemanların aynı sayıda sabit bir vektör olan , X ve nokta gösterir nokta ürün tek değişkenli Gauss ile, . Bu sonuç kullanılarak aşağıdaki


Pozitif-kesinlik nasıl gözlemleyin Σ nokta ürünün varyans pozitif olmalıdır anlamına gelir.
Bir benzeşik transformasyon X, örneğin 2 , X ile aynı değildir , iki bağımsız gerçekleşmeleri toplamı arasında X .
geometrik yorumlama
Tekil olmayan çok değişkenli normal dağılımın denklik konturları , ortalamada ortalanmış elipsoidlerdir (yani hiperkürelerin lineer dönüşümleri ). Dolayısıyla çok değişkenli normal dağılım, eliptik dağılımlar sınıfına bir örnektir . Elipsoidlerin asal eksenlerinin yönleri kovaryans matrisinin özvektörleri tarafından verilir . Asal eksenlerin karesi alınmış göreli uzunlukları, karşılık gelen özdeğerlerle verilir.

Eğer Σ = UΛU T = UΛ 1/2 ( UΛ 1/2 ) , T bir bir eigendecomposition sütunları U birimi özvektörleri ve Λ a, köşegen matris sonra biz, özdeğerler

Ayrıca, U bir olması seçilebilir rotasyon matrisi bir eksen tersini üzerinde herhangi bir etkisi yok gibi, N (0, Λ ), ancak bir sütun tersine çevrilmesi işareti değiştirir u' in belirleyici. Dağıtım , N ( μ , Σ ) geçerli olan , N (0 I tarafından ölçülen) X 1/2 , döndürülebilir U ve Çeviri u .
Tersine, herhangi bir μ , tam sıralı matris U ve pozitif diyagonal girişler Λ i seçimi, tekil olmayan çok değişkenli bir normal dağılım verir. Herhangi bir X ise i sıfırdır ve u elde edilen kovaryans matrisi, kare UΛU T olan tekil . Geometrik olarak bu , asal eksenlerden en az birinin uzunluğu sıfır olduğundan , her kontur elipsoidinin sonsuz derecede ince olduğu ve n boyutlu uzayda sıfır hacme sahip olduğu anlamına gelir ; bu dejenere bir durumdur .
" Kutupsal koordinatlarda (yarıçap ve açı) yeniden yazılan, iki değişkenli normal bir rastgele değişkende gerçek ortalamanın etrafındaki yarıçap, bir Hoyt dağılımını izler ."
Bir boyutta aralıkta normal dağılıma ait bir örnek bulma olasılığı yaklaşık olarak %68,27'dir, ancak daha yüksek boyutlarda standart sapma elipsi bölgesinde bir örnek bulma olasılığı daha düşüktür.

| Boyutluluk |
olasılık
|
| 1 |
0.6827
|
| 2 |
0.3935
|
| 3 |
0.1987
|
| 4 |
0.0902
|
| 5 |
0.0374
|
| 6 |
0.0144
|
| 7 |
0.0052
|
| 8 |
0.0018
|
| 9 |
0.0006
|
| 10 |
0.0002
|
İstatiksel sonuç
parametre tahmini
Çok değişkenli bir normal dağılımın kovaryans matrisinin maksimum olabilirlik tahmin edicisinin türetilmesi basittir.
Kısacası, çok değişkenli bir normalin olasılık yoğunluk fonksiyonu (pdf),

ve bir n gözlem
örneğinden elde edilen kovaryans matrisinin ML tahmincisi

bu sadece örnek kovaryans matrisidir . Bu, beklentisi olan yanlı bir tahmin edicidir .
![E[\widehat{\boldsymbol\Sigma}] = \frac{n-1}{n} \boldsymbol\Sigma.](https://wikimedia.org/api/rest_v1/media/math/render/svg/bacdf39e0509492e90dbb2fb2fdcaac78ca196db)
Tarafsız bir örnek kovaryansı
-
![{\displaystyle {\widehat {\boldsymbol {\Sigma }}}={\frac {1}{n-1}}\sum _{i=1}^{n}(\mathbf {x} _{i} -{\overline {\mathbf {x} }})(\mathbf {x} _{i}-{\overline {\mathbf {x} }})^{\rm {T}}={\frac {1 }{n-1}}\sol[X'\sol(I-{\frac {1}{n}}\cdot J\sağ)X\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b483843b0f64ecbfea751011ef0ab8e61c7f0dcc) (matris biçimi, bir birim matris, J a, parantez içinde terim bu nedenle,; olanlar matris merkezleme matris)
(matris biçimi, bir birim matris, J a, parantez içinde terim bu nedenle,; olanlar matris merkezleme matris)



Fisher bilgi matrisi çok değişkenli bir normal dağılım parametrelerinin hesaplanması için bir kapalı bir ifade yer alır. Bu, örneğin, bu ayarda parametre tahmini için Cramér–Rao sınırını hesaplamak için kullanılabilir . Daha fazla ayrıntı için Fisher bilgilerine bakın.
Bayes çıkarımı
Gelen Bayes istatistikleri , eşlenik önce ortalama vektörün bir çok değişkenli normal dağılım ve kovaryans matrisinin eşlenik önce bir bir ters-Wishart dağılımı . O zaman n gözlem yapıldığını
varsayalım.

ve önceden bir eşlenik atanmışsa, burada

nerede

ve

Sonra,

nerede

Çok değişkenli normallik testleri
Çok değişkenli normallik testleri, çok değişkenli normal dağılıma benzerlik için belirli bir veri setini kontrol eder . Boş hipotez olmasıdır veri seti normal dağılım benzerdir, bu yüzden, yeterince küçük bir p -değeri normal olmayan verilerini gösterir. Çok değişkenli normallik testleri, Cox-Small testi ve Smith ve Jain'in Larry Rafsky ve Jerome Friedman tarafından oluşturulan Friedman-Rafsky testinin uyarlamasını içerir .
Mardia'nın testi , çarpıklık ve basıklık ölçümlerinin çok değişkenli uzantılarına dayanmaktadır . Bir { x 1 , ..., x n } k boyutlu vektör örneği için hesaplıyoruz
![\begin{align} & \widehat{\boldsymbol\Sigma} = {1 \over n} \sum_{j=1}^n \left(\mathbf{x}_j - \bar{\mathbf{x}}\ sağ)\left(\mathbf{x}_j - \bar{\mathbf{x}}\sağ)^T \\ & A = {1 \over 6n} \sum_{i=1}^n \sum_{j =1}^n \left[ (\mathbf{x}_i - \bar{\mathbf{x}})^T\;\widehat{\boldsymbol\Sigma}^{-1} (\mathbf{x}_j - \bar{\mathbf{x}}) \right]^3 \\ & B = \sqrt{\frac{n}{8k(k+2)}}\left\{{1 \over n} \sum_ {i=1}^n \left[ (\mathbf{x}_i - \bar{\mathbf{x}})^T\;\widehat{\boldsymbol\Sigma}^{-1} (\mathbf{x }_i - \bar{\mathbf{x}}) \sağ]^2 - k(k+2) \sağ\} \end{hiza}](https://wikimedia.org/api/rest_v1/media/math/render/svg/379e5ee62d84b83c7e77088847f4855f6e6b1fed)
Çok değişkenli normalliğin sıfır hipotezi altında, A istatistiği yaklaşık olarak bir ki-kare dağılımına sahip olacaktır.
1/6⋅ k ( k + 1)( k + 2) serbestlik derecesi ve B yaklaşık olarak standart normal N (0,1) olacaktır.
Mardia'nın basıklık istatistiği çarpıktır ve sınırlayıcı normal dağılıma çok yavaş yakınsar. Orta büyüklükteki örnekler için , basıklık istatistiğinin asimptotik dağılımının parametreleri değiştirilir. Küçük örneklem testleri için ( ) ampirik kritik değerler kullanılır. Her iki istatistik için de kritik değer tabloları Rencher tarafından k = 2, 3, 4 için verilmiştir.


Mardia'nın testleri afin değişmezdir ancak tutarlı değildir. Örneğin, çok değişkenli çarpıklık testi, simetrik normal olmayan alternatiflere karşı tutarlı değildir.
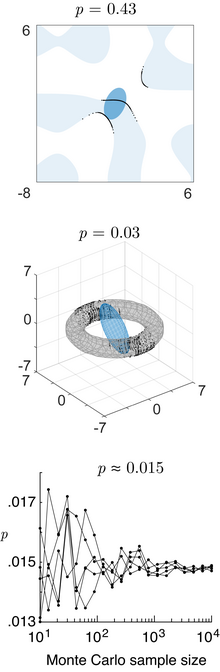
BHEP testi deneysel arasındaki farkın norm hesaplar karakteristik fonksiyonu ve normal dağılım teorik karakteristik fonksiyonu. Normun hesaplanması , Gauss ağırlıklandırma fonksiyonuna göre kare-integre edilebilir fonksiyonların L 2 ( μ ) uzayında yapılır . Test istatistiği


Bu test istatistiğinin sınırlayıcı dağılımı, ki-kare rasgele değişkenlerin ağırlıklı bir toplamıdır, ancak pratikte, Monte-Carlo simülasyonlarını kullanarak örnek niceliklerini hesaplamak daha uygundur.
Bunlara ve diğer test prosedürlerine ilişkin ayrıntılı bir araştırma mevcuttur.
Çok değişkenli normal sınıflara sınıflandırma
Gauss Diskriminant Analizi
Varsayalım ki gözlemler (vektörler), bilinen ortalamalar ve kovaryanslar ile birkaç çok değişkenli normal dağılımdan birinden geldiği varsayılmaktadır. Daha sonra herhangi bir gözlem, ortaya çıkma olasılığının en yüksek olduğu dağılıma atanabilir. Bu sınıflandırma prosedürüne Gauss diskriminant analizi denir. Sınıflandırma performansı, yani farklı sınıflandırma sonuçlarının olasılıkları ve genel sınıflandırma hatası, ışın izlemenin sayısal yöntemiyle ( Matlab kodu ) hesaplanabilir .
hesaplama yöntemleri
Dağılımdan değer çizme
Rasgele vektör çizimi (numune) için yaygın olarak kullanılan bir yöntem, x den K ortalama vektörü ile boyutlu çok değişkenli normal dağılım ^ ı ve kovaryans matrisi Σ aşağıdaki gibi çalışır:
- A A T = Σ olan herhangi bir gerçek A matrisini bulun . Tüm Σ pozitif kesin, Choleskey ayrışma , tipik olarak kullanılır ve geniş bir şekilde , uygun bir matriks her iki durumda da (kovaryans matrisi yarı tanımlı tek olumlu olabilir), bu ayrışım sürekli olarak, bir elde edilir. Alternatif bir matris kullanmaktır A = UΛ yarım bir elde edilen spektral ayrışma Σ = UΛU -1 arasında Σ . Birinci yaklaşım sayısal olarak daha basittir, ancak matrisler bir ikinci yaklaşım basit yeniden orderings ile ilgili matrisler verirken, rasgele vektörün elemanlarının farklı sıralamalar için değiştirmek. Teoride her iki yaklaşım da uygun bir matris A belirlemek için eşit derecede iyi yollar verir , ancak hesaplama süresinde farklılıklar vardır.
- Let z = ( z 1 , ..., z , N ) T olan bileşenleri için bir vektör olarak , N , bağımsız standart normal (kullanarak, örneğin, oluşturulabilir değişkenler Kutu Muller dönüşümü ).
- Let x olmak μ + Az . Bu, afin dönüşüm özelliği nedeniyle istenen dağılıma sahiptir.
Ayrıca bakınız
Referanslar
Edebiyat





![{\displaystyle {\boldsymbol {\mu }}=\left[{\begin{smallmatrix}0\\0\end{smallmatrix}}\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/288f20c89fee827ad086cec03369439ba3615d7f)
![{\displaystyle {\boldsymbol {\Sigma }}=\left[{\begin{smallmatrix}1&3/5\\3/5&2\end{smallmatrix}}\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee3a76f734b37fcce91f30617152fe104b2782bc)








![{\displaystyle {\boldsymbol {\mu }}=\operatöradı {E} [\mathbf {X} ]=(\operatöradı {E} [X_{1}],\operatöradı {E} [X_{2}], \ldots ,\operatöradı {E} [X_{k}])^{\textbf {T}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e69e434645f47377bc8766624255c8026adf7964)

![{\displaystyle \Sigma _{i,j}=\operatöradı {E} [(X_{i}-\mu _{i})(X_{j}-\mu _{j})]=\operatöradı {Cov } [X_{i},X_{j}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c970083f8469366521881996464f23d376b7c40b)































![{\görüntüleme stili {\metin{[XY]′}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24925a0dd360004248b2a1de70e2b0bcf3fcf687)
![{\displaystyle f(x,y)={\frac {1}{2\pi \sigma _{X}\sigma _{Y}{\sqrt {1-\rho ^{2}}}}}\exp \left(-{\frac {1}{2(1-\rho ^{2})}}\left[\left({\frac {x-\mu _{X}}{\sigma _{X}) }}\sağ)^{2}-2\rho \left({\frac {x-\mu _{X}}{\sigma _{X}}}\sağ)\sol({\frac {y- \mu _{Y}}{\sigma _{Y}}}\sağ)+\sol({\frac {y-\mu _{Y}}{\sigma _{Y}}}\sağ)^{ 2}\sağ]\sağ)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c616921276f29c0c0cd5383fd81045939f8f6e82)





































![{\displaystyle \mu _{1,\ldots ,N}(\mathbf {x} )\ {\stackrel {\mathrm {def} }{=}}\ \mu _{r_{1},\ldots ,r_ {N}}(\mathbf {x} )\ {\stackrel {\mathrm {def} }{=}}\operatöradı {E} \left[\prod _{j=1}^{N}X_{j} ^{r_{j}}\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68bafb23658afe2f4246d5f27781aac7eeacbaa7)


![{\displaystyle {\begin{hizalanmış}&\operatöradı {E} [X_{1}X_{2}X_{3}X_{4}X_{5}X_{6}]\\[8pt]={}& \operatöradı {E} [X_{1}X_{2}]\operatöradı {E} [X_{3}X_{4}]\operatöradı {E} [X_{5}X_{6}]+\operatöradı {E } [X_{1}X_{2}]\operatöradı {E} [X_{3}X_{5}]\operatöradı {E} [X_{4}X_{6}]+\operatöradı {E} [X_{ 1}X_{2}]\operatöradı {E} [X_{3}X_{6}]\operatöradı {E} [X_{4}X_{5}]\\[4pt]&{}+\operatöradı {E } [X_{1}X_{3}]\operatöradı {[} X_{2}X_{4}]\operatöradı {E} [X_{5}X_{6}]+\operatöradı {E} [X_{1 }X_{3}]\operatöradı {E} [X_{2}X_{5}]\operatöradı {E} [X_{4}X_{6}]+\operatöradı {E} [X_{1}X_{3 }]\operatöradı {E} [X_{2}X_{6}]\operatöradı {E} [X_{4}X_{5}]\\[4pt]&{}+\operatöradı {E} [X_{1 }X_{4}]\operatöradı {E} [X_{2}X_{3}]\operatöradı {E} [X_{5}X_{6}]+\operatöradı {E} [X_{1}X_{4 }]\operatöradı {E} [X_{2}X_{5}]\operatöradı {E} [X_{3}X_{6}]+\operatöradı {E} [X_{1}X_{4}]\operatöradı {E} [X_{2}X_{6}]\operatöradı {E} [X_{3}X_{5}]\\[4pt]&{}+\operatöradı {E} [X_{1}X_{5 }]\operatöradı {E} [X_{2}X_{3} ]\operatöradı {E} [X_{4}X_{6}]+\operatöradı {E} [X_{1}X_{5}]\operatöradı {E} [X_{2}X_{4}]\operatöradı { E} [X_{3}X_{6}]+\operatöradı {E} [X_{1}X_{5}]\operatöradı {E} [X_{2}X_{6}]\operatöradı {E} [X_ {3}X_{4}]\\[4pt]&{}+\operatöradı {E} [X_{1}X_{6}]\operatöradı {E} [X_{2}X_{3}]\operatöradı { E} [X_{4}X_{5}]+\operatöradı {E} [X_{1}X_{6}]\operatöradı {E} [X_{2}X_{4}]\operatöradı {E} [X_ {3}X_{5}]+\operatöradı {E} [X_{1}X_{6}]\operatöradı {E} [X_{2}X_{5}]\operatöradı {E} [X_{3}X_ {4}].\end{hizalanmış}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec24a2d6baf16b88926e5e83fb8e4005c5a2541a)

![{\displaystyle [1,\ldots ,2\lambda ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a605bf32a38577fe9df1bc5715a4a3cac5869832)
![{\displaystyle {\begin{hizalanmış}\operatöradı {E} \sol[X_{i}^{4}\sağ]&=3\sigma _{ii}^{2}\\[4pt]\operatöradı {E } \left[X_{i}^{3}X_{j}\sağ]&=3\sigma _{ii}\sigma _{ij}\\[4pt]\operatöradı {E} \left[X_{i }^{2}X_{j}^{2}\sağ]&=\sigma _{ii}\sigma _{jj}+2\sigma _{ij}^{2}\\[4pt]\operatöradı { E} \left[X_{i}^{2}X_{j}X_{k}\sağ]&=\sigma _{ii}\sigma _{jk}+2\sigma _{ij}\sigma _{ ik}\\[4pt]\operatöradı {E} \left[X_{i}X_{j}X_{k}X_{n}\right]&=\sigma _{ij}\sigma _{kn}+\ sigma _{ik}\sigma _{jn}+\sigma _{in}\sigma _{jk}.\end{hizalı}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e08f5bc180e3f1f4379c1026100e833ea85de97)

![{\displaystyle E\sol[X_{i}X_{j}X_{k}X_{n}\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b4bbbf2becaf15b246898e928a37e7d0ab6f93a)
![{\displaystyle \operatöradı {E} [X_{i}^{2}X_{k}X_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7bc1920d0e524aa567ca471bdb54dcf7ef7e673)














![{\displaystyle \ln L({\boldsymbol {x}})=-{\frac {1}{2}}\left[\ln(|{\boldsymbol {\Sigma }}}|\,)+({\ boldsymbol {x}}-{\boldsymbol {\mu }})'{\boldsymbol {\Sigma }}^{-1}({\boldsymbol {x}}-{\boldsymbol {\mu }})+k\ ln(2\pi )\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ad05643016bbf6ac76a826320bea00704b50982)



























































![E[\widehat{\boldsymbol\Sigma}] = \frac{n-1}{n} \boldsymbol\Sigma.](https://wikimedia.org/api/rest_v1/media/math/render/svg/bacdf39e0509492e90dbb2fb2fdcaac78ca196db)
![{\displaystyle {\widehat {\boldsymbol {\Sigma }}}={\frac {1}{n-1}}\sum _{i=1}^{n}(\mathbf {x} _{i} -{\overline {\mathbf {x} }})(\mathbf {x} _{i}-{\overline {\mathbf {x} }})^{\rm {T}}={\frac {1 }{n-1}}\sol[X'\sol(I-{\frac {1}{n}}\cdot J\sağ)X\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b483843b0f64ecbfea751011ef0ab8e61c7f0dcc)









![\begin{align} & \widehat{\boldsymbol\Sigma} = {1 \over n} \sum_{j=1}^n \left(\mathbf{x}_j - \bar{\mathbf{x}}\ sağ)\left(\mathbf{x}_j - \bar{\mathbf{x}}\sağ)^T \\ & A = {1 \over 6n} \sum_{i=1}^n \sum_{j =1}^n \left[ (\mathbf{x}_i - \bar{\mathbf{x}})^T\;\widehat{\boldsymbol\Sigma}^{-1} (\mathbf{x}_j - \bar{\mathbf{x}}) \right]^3 \\ & B = \sqrt{\frac{n}{8k(k+2)}}\left\{{1 \over n} \sum_ {i=1}^n \left[ (\mathbf{x}_i - \bar{\mathbf{x}})^T\;\widehat{\boldsymbol\Sigma}^{-1} (\mathbf{x }_i - \bar{\mathbf{x}}) \sağ]^2 - k(k+2) \sağ\} \end{hiza}](https://wikimedia.org/api/rest_v1/media/math/render/svg/379e5ee62d84b83c7e77088847f4855f6e6b1fed)







