Doğrusal regresyon - Linear regression
| Bir serinin parçası |
| Regresyon analizi |
|---|
| Modeller |
| Tahmin |
| Arka plan |
Olarak istatistik , lineer regresyon a, doğrusal bir ilişkisini modellemek için bir yaklaşım skalar tepki ve bir veya daha fazla açıklayıcı değişkenler (aynı zamanda bağımlı ve bağımsız değişkenlerin ). Bir açıklayıcı değişkenin durumuna basit doğrusal regresyon denir ; birden fazla için, sürece çoklu doğrusal regresyon denir . Bu terim, tek bir skaler değişken yerine birden çok ilişkili bağımlı değişkenin tahmin edildiği çok değişkenli doğrusal regresyondan farklıdır .
Doğrusal regresyon, ilişkiler kullanılarak modellenmiştir doğrusal tahmin işlevleri olan bilinmeyen modeli parametreleri olan tahmini gelen veriler . Bu tür modellere doğrusal modeller denir . En yaygın olarak, açıklayıcı değişkenlerin (veya tahmin edicilerin) değerleri verilen yanıtın koşullu ortalamasının , bu değerlerin afin bir fonksiyonu olduğu varsayılır ; daha az yaygın olarak, koşullu medyan veya başka bir nicelik kullanılır. Tüm regresyon analizi formları gibi , lineer regresyon , çok değişkenli analizin alanı olan tüm bu değişkenlerin ortak olasılık dağılımından ziyade, tahmin edicilerin değerleri verilen yanıtın koşullu olasılık dağılımına odaklanır .
Doğrusal regresyon, titizlikle çalışılan ve pratik uygulamalarda yaygın olarak kullanılan ilk tip regresyon analiziydi. Bunun nedeni, bilinmeyen parametrelerine doğrusal olarak bağlı modellerin, parametreleriyle doğrusal olmayan ilişkili modellere göre daha kolay uydurulması ve elde edilen tahmin edicilerin istatistiksel özelliklerinin belirlenmesinin daha kolay olmasıdır.
Doğrusal regresyonun birçok pratik kullanımı vardır. Çoğu uygulama aşağıdaki iki geniş kategoriden birine girer:
- Hedef tahmin , tahmin veya hata azaltma ise, tahmine dayalı bir modeli yanıtın ve açıklayıcı değişkenlerin gözlenen bir veri kümesine uydurmak için doğrusal regresyon kullanılabilir . Böyle bir model geliştirdikten sonra, açıklayıcı değişkenlerin ek değerleri eşlik eden bir yanıt değeri olmadan toplanırsa, uygun model yanıtın bir tahminini yapmak için kullanılabilir.
- Amaç, açıklayıcı değişkenlerdeki varyasyona atfedilebilecek yanıt değişkenindeki varyasyonu açıklamaksa, yanıt ile açıklayıcı değişkenler arasındaki ilişkinin gücünü ölçmek ve özellikle bazı değişkenlerin olup olmadığını belirlemek için doğrusal regresyon analizi uygulanabilir. açıklayıcı değişkenlerin yanıtla hiçbir doğrusal ilişkisi olmayabilir veya açıklayıcı değişkenlerin hangi alt kümelerinin yanıt hakkında fazla bilgi içerebileceğini belirlemek için.
Doğrusal regresyon modelleri genellikle en küçük kareler yaklaşımı kullanılarak uydurulur , ancak başka bir normdaki "uyum eksikliğini" en aza indirerek ( en küçük mutlak sapmalar regresyonunda olduğu gibi) veya cezalı bir sırt regresyonunda olduğu gibi en küçük kareler maliyet fonksiyonunun versiyonu ( L 2 - norm cezası) ve kement ( L 1 - norm cezası). Tersine, en küçük kareler yaklaşımı, doğrusal olmayan modeller için kullanılabilir. Bu nedenle, "en küçük kareler" ve "doğrusal model" terimleri yakından bağlantılı olmasına rağmen, eş anlamlı değildir.
formülasyon
Verilen Bir veri seti arasında N istatistik birimlerinin bir doğrusal regresyon modeli bağımlı değişken arasındaki ilişki olduğunu varsayar y ve p -vector Regresör x olan doğrusal . Bu ilişki, bir bozucu terim veya hata değişkeni ε ile modellenir - bağımlı değişken ve regresörler arasındaki doğrusal ilişkiye "gürültü" ekleyen gözlemlenmemiş bir rastgele değişken . Böylece model şeklini alır.
burada T devrik anlamına gelir , böylece x i T β , x i ve β vektörleri arasındaki iç çarpımdır .
Genellikle bu n denklemler birlikte istiflenir ve matris notasyonunda şu şekilde yazılır:
nerede
Notasyon ve terminoloji
- regresand , endojen değişken , yanıt değişkeni , ölçülen değişken , kriter değişkeni veya bağımlı değişken olarak adlandırılan değişkenin gözlenen değerlerinin bir vektörüdür . Bu değişken bazen tahmin edilen değişken olarak da bilinir , ancak bu , belirtilen tahmin edilen değerlerle karıştırılmamalıdır . Bir veri setindeki hangi değişkenin bağımlı değişken, hangilerinin bağımsız değişken olarak modelleneceğine ilişkin karar, değişkenlerden birinin değerinin diğer değişkenlerden kaynaklandığı veya doğrudan onlardan etkilendiği varsayımına dayanabilir. Alternatif olarak, değişkenlerden birini diğerlerine göre modellemek için operasyonel bir neden olabilir, bu durumda nedensellik varsayımına gerek yoktur.
-
regresörler , dışsal değişkenler , açıklayıcı değişkenler , ortak değişkenler , girdi değişkenleri , öngörücü değişkenler veya bağımsız değişkenler (kavramla karıştırılmamalıdır) olarak bilinen satır vektörlerinin veya n -boyutlu sütun vektörlerinin bir matrisi olarak görülebilir. ve bağımsız rastgele değişken ). Matris bazen tasarım matrisi olarak adlandırılır .
- Genellikle bir sabit, regresörlerden biri olarak dahil edilir. için özellikle .
- Bazen regresörlerden biri, polinom regresyon ve parçalı regresyonda olduğu gibi, başka bir regresörün veya verilerin doğrusal olmayan bir fonksiyonu olabilir . Model, β parametre vektöründe doğrusal olduğu sürece doğrusal kalır .
- Değerleri x ij ya gözlenen değerler olarak görülebilir rastgele değişkenler X j önce veya bağımlı değişken gözlemleyerek için seçilen sabit değerler olarak. Her iki yorum da farklı durumlarda uygun olabilir ve genellikle aynı tahmin prosedürlerine yol açarlar; ancak bu iki durumda asimptotik analize farklı yaklaşımlar kullanılmaktadır.
Belirli bir veri kümesine doğrusal bir model uydurmak genellikle regresyon katsayılarının hata terimini en aza indirecek şekilde tahmin edilmesini gerektirir . Örneğin, kareleri alınmış hataların toplamını minimizasyon için bir ölçü olarak kullanmak yaygındır .
Örnek
Küçük bir topun havaya fırlatıldığı bir durumu ele alalım ve sonra onun yükselme yüksekliklerini t i zamanının çeşitli anlarında h i ölçelim . Fizik bize, sürtünmeyi göz ardı ederek, ilişkinin şu şekilde modellenebileceğini söylüyor:
burada β 1 topun başlangıç hızını belirler, β 2 standart yerçekimi ile orantılıdır ve ε i ölçüm hatalarından kaynaklanır. Doğrusal regresyon , ölçülen verilerden β 1 ve β 2 değerlerini tahmin etmek için kullanılabilir . Bu model zaman değişkeninde doğrusal değildir, ancak β 1 ve β 2 parametrelerinde doğrusaldır ; regresörleri alırsak x i = ( x ben 1 , x ben 2 ) = ( t ben , t ben 2 ), model standart formu alır
varsayımlar
Standart tahmin tekniklerine sahip standart doğrusal regresyon modelleri, tahmin değişkenleri, yanıt değişkenleri ve bunların ilişkileri hakkında bir takım varsayımlarda bulunur. Bu varsayımların her birinin gevşetilmesine (yani daha zayıf bir forma indirgenmesine) ve bazı durumlarda tamamen ortadan kaldırılmasına izin veren çok sayıda uzantı geliştirilmiştir. Genellikle bu uzantılar, tahmin prosedürünü daha karmaşık ve zaman alıcı hale getirir ve aynı zamanda eşit derecede kesin bir model üretmek için daha fazla veri gerektirebilir.
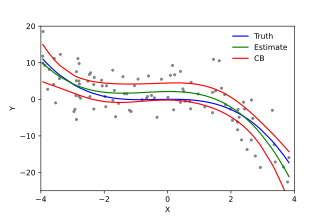
Aşağıdakiler, standart tahmin teknikleriyle (örneğin, sıradan en küçük kareler ) standart doğrusal regresyon modelleri tarafından yapılan başlıca varsayımlardır :
- Zayıf dışsallık . Bu temelde, tahmin değişkenleri x'in rastgele değişkenler yerine sabit değerler olarak ele alınabileceği anlamına gelir . Bu, örneğin, tahmin değişkenlerinin hatasız, yani ölçüm hatalarıyla kontamine olmadığı varsayıldığı anlamına gelir. Bu varsayım birçok durumda gerçekçi olmasa da, onu bırakmak, değişkenlerde hata modellerini önemli ölçüde daha zor hale getirir .
- Doğrusallık . Bu, yanıt değişkeninin ortalamasının , parametrelerin (regresyon katsayıları) ve öngörücü değişkenlerin doğrusal bir kombinasyonu olduğu anlamına gelir . Bu varsayımın ilk bakışta göründüğünden çok daha az kısıtlayıcı olduğunu unutmayın. Tahmin değişkenleri sabit değerler olarak ele alındığından (yukarıya bakın), doğrusallık gerçekten sadece parametreler üzerinde bir kısıtlamadır. Tahmin değişkenlerinin kendileri keyfi olarak dönüştürülebilir ve aslında aynı temel tahmin değişkeninin birden çok kopyası eklenebilir, her biri farklı şekilde dönüştürülür. Bu teknik, örneğin, yanıt değişkenine bir tahmin değişkeninin keyfi bir polinom işlevi (belirli bir sıraya kadar) olarak sığdırmak için doğrusal regresyon kullanan polinom regresyonunda kullanılır . Bu kadar esneklikle, polinom regresyonu gibi modeller genellikle "çok fazla güce" sahiptir, çünkü verilere fazla uyma eğilimi gösterirler . Sonuç olarak, tahmin sürecinden mantıksız çözümlerin çıkmasını önlemek için tipik olarak bir tür düzenlileştirme kullanılmalıdır. Yaygın örnekler, sırt regresyonu ve kement regresyonudur . Doğası gereği aşırı uyum sorununa az ya da çok bağışık olan Bayes doğrusal regresyon da kullanılabilir. (Aslında, sırt regresyon ve kement regresyon hem belirli tipleri ile, regresyon doğrusal Bayesian özel durumlarda olarak görülebilir önce dağılımları regresyon katsayısı yerleştirilir.)
- Sabit varyans (diğer adıyla homoscedasticity ). Bu, hataların varyansının tahmin değişkenlerinin değerlerine bağlı olmadığı anlamına gelir. Bu nedenle, tahmin edicilerin verilen sabit değerleri için yanıtların değişkenliği, yanıtların ne kadar büyük veya küçük olduğuna bakılmaksızın aynıdır. Ortalaması büyük olan bir değişken, ortalaması küçük olandan daha büyük bir varyansa sahip olacağından, genellikle durum böyle değildir. Örneğin, geliri 100.000 ABD Doları olduğu tahmin edilen bir kişinin gerçek geliri kolayca 80.000 ABD Doları veya 120.000 ABD Doları - yani yaklaşık 20.000 ABD Doları tutarında bir standart sapma - olabilirken , tahmini geliri 10.000 ABD Doları olan başka bir kişinin aynı 20.000 ABD Doları standart sapmaya sahip olması olası değildir. , çünkü bu, gerçek gelirlerinin -10.000 ile 30.000 ABD Doları arasında herhangi bir yerde değişebileceği anlamına gelir. (Aslında, bunun da gösterdiği gibi, çoğu durumda - genellikle normal dağılmış hataların varsayımının başarısız olduğu aynı durumlarda - varyans veya standart sapmanın sabitten ziyade ortalamayla orantılı olduğu tahmin edilmelidir.) Eş varyanslılığın olmaması heteroskedastisite denir . Bu varsayımı kontrol etmek için, tahmin edilen değerlere (veya her bir tahmin edicinin değerlerine) karşı artıkların bir grafiği bir "fan etkisi" (yani, grafik üzerinde soldan sağa hareket ettikçe artan veya azalan dikey yayılma) için incelenebilir. . Tahmin edilen değerlere (veya her tahmin ediciye) karşı mutlak veya kare artıkların bir grafiği de bir eğilim veya eğrilik için incelenebilir. Resmi testler de kullanılabilir; bkz. Heteroskedastisite . Değişen varyansın mevcudiyeti, gerçek varyans yapısını hesaba katan bir tahmin yerine, genel bir "ortalama" varyans tahmininin kullanılmasıyla sonuçlanacaktır. Bu, daha az kesinliğe (ancak olağan en küçük kareler durumunda, sapmalı değil) parametre tahminlerine ve taraflı standart hatalara yol açarak yanıltıcı testler ve aralık tahminleri ile sonuçlanır. Ortalama karesel hata modeli için de yanlış olacaktır. Ağırlıklı en küçük kareler ve değişen varyansla tutarlı standart hataların kullanımı dahil olmak üzere çeşitli tahmin teknikleri değişen varyansla oldukça genel bir şekilde başa çıkabilir. Bayes doğrusal regresyon teknikleri, varyansın ortalamanın bir fonksiyonu olduğu varsayıldığında da kullanılabilir. Bazı durumlarda, (yanıt değişkeni için bir dönüşümü uygulanarak sorunu çözmek için de mümkündür, örneğin, uydurma logaritmasını yanıt değişkeni kendisi olduğunu ima doğrusal regresyon modeli kullanılarak yanıt değişkenin, log-normal dağılımı yerine bir normal dağılım ).
-
Hataların bağımsızlığı . Bu, yanıt değişkenlerinin hatalarının birbiriyle ilişkisiz olduğunu varsayar. (Gerçek istatistiksel bağımsızlık , yalnızca korelasyon eksikliğinden daha güçlü bir koşuldur ve geçerli olduğu biliniyorsa kullanılabilir olmasına rağmen, genellikle gerekli değildir.) Genelleştirilmiş en küçük kareler gibi bazı yöntemler , genellikle gerektirse de, ilişkili hataları ele alabilir. modeli ilintisiz hataları varsaymaya yönlendirmek için bir tür düzenlileştirme kullanılmadığı sürece önemli ölçüde daha fazla veri . Bayes doğrusal regresyon , bu sorunu ele almanın genel bir yoludur.
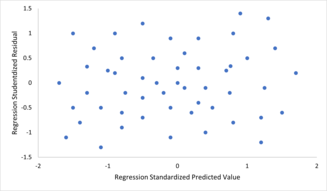 Bir doğrusal regresyon modeli içinde doğrusallık, sabit varyans ve hataların bağımsızlığı varsayımlarının ihlallerini kontrol etmek için, artıklar tipik olarak tahmin edilen değerlere (veya bireysel tahmin edicilerin her birine) karşı çizilir. 0'da yatay orta hat etrafında noktaların görünüşte rastgele bir dağılımı idealdir, ancak hatalardaki otokorelasyon veya bunların bir veya daha fazla ortak değişkenle korelasyonu gibi belirli türdeki ihlalleri ekarte edemez .
Bir doğrusal regresyon modeli içinde doğrusallık, sabit varyans ve hataların bağımsızlığı varsayımlarının ihlallerini kontrol etmek için, artıklar tipik olarak tahmin edilen değerlere (veya bireysel tahmin edicilerin her birine) karşı çizilir. 0'da yatay orta hat etrafında noktaların görünüşte rastgele bir dağılımı idealdir, ancak hatalardaki otokorelasyon veya bunların bir veya daha fazla ortak değişkenle korelasyonu gibi belirli türdeki ihlalleri ekarte edemez . - Tahmin edicilerde mükemmel çoklu bağlantı eksikliği . Standart en küçük kareler tahmin yöntemleri için tasarım matrisi X'in tam sütun sırası p olmalıdır ; aksi takdirde , öngörücü değişkenlerde mükemmel çoklu bağlantı vardır, yani iki veya daha fazla öngörücü değişken arasında doğrusal bir ilişki vardır. Bu, orijinal ile birlikte bir değişkenin doğrusal bir dönüşümünü kullanarak (örneğin, Fahrenhayt ve Santigrat olarak ifade edilen aynı sıcaklık ölçümleri) veya modelde birden çok değişkenin doğrusal bir kombinasyonunu dahil ederek, verilerdeki bir değişkeni yanlışlıkla çoğaltmaktan kaynaklanabilir, onların ortalamaları gibi. Ayrıca, tahmin edilecek parametre sayısına kıyasla çok az veri mevcutsa (örneğin, regresyon katsayılarından daha az veri noktası) olabilir. Tahmin edicilerin yüksek oranda ancak mükemmel bir şekilde ilişkili olmadığı bu varsayımın neredeyse ihlal edilmesi, parametre tahminlerinin kesinliğini azaltabilir (bkz. Varyans enflasyon faktörü ). Mükemmel çoklu bağlantı durumunda, parametre vektörü β olacak tanımlanabilir olmayan -it bir benzersiz bir çözüm vardır. Böyle bir durumda, sadece parametrelerin bir (diğer bir deyişle, bunların değerleri sadece tam parametre alanı bazı doğrusal bölme odası içinde tahmin edilebilir tespit edilebilir R p ). Kısmi en küçük kareler regresyonuna bakın . Bazıları "etki seyrekliği" (etkilerin büyük bir bölümünün tam olarak sıfır olduğu) gibi ek varsayımlar gerektiren çoklu bağlantıya sahip doğrusal modelleri uydurmak için yöntemler geliştirilmiştir. Genelleştirilmiş doğrusal modellerde kullanılanlar gibi parametre tahmini için hesaplama açısından daha pahalı yinelenen algoritmaların bu sorundan etkilenmediğine dikkat edin.
Bu varsayımların ötesinde, verilerin diğer bazı istatistiksel özellikleri, farklı tahmin yöntemlerinin performansını güçlü bir şekilde etkiler:
- Hata terimleri ve regresörler arasındaki istatistiksel ilişki, bir tahmin prosedürünün yansız ve tutarlı olma gibi istenen örnekleme özelliklerine sahip olup olmadığını belirlemede önemli bir rol oynar.
- Tahmin değişkenlerinin x düzenlemesi veya olasılık dağılımı , β tahminlerinin kesinliği üzerinde büyük bir etkiye sahiptir . Örnekleme ve deney tasarımı, kesin bir β tahmini elde edecek şekilde veri toplamak için rehberlik sağlayan oldukça gelişmiş istatistik alt alanlarıdır .
Tercüme

Modeldeki diğer tüm tahmin değişkenleri "sabit tutulduğunda", tek bir tahmin değişkeni x j ile yanıt değişkeni y arasındaki ilişkiyi tanımlamak için uygun bir doğrusal regresyon modeli kullanılabilir . Spesifik olarak, yorumlanması β j olan beklenen değişiklik y bir tek birimlik bir değişime karşılık x j diğer ortak değişkenlerinin sabit olduğu, beklenen değer tutulan kısmi türevi ve y ile ilgili olarak x j . Bu bazen denir benzersiz etkisi ait x j üzerine y . Buna karşılık, x j'nin y üzerindeki marjinal etkisi , yalnızca x j ile y arasında ilişki kuran bir korelasyon katsayısı veya basit doğrusal regresyon modeli kullanılarak değerlendirilebilir ; bu etki toplam türev ve y ile ilgili olarak x j .
Regresyon sonuçları yorumlanırken dikkatli olunmalıdır, çünkü bazı regresörler marjinal değişikliklere izin vermeyebilir ( kukla değişkenler veya kesme terimi gibi), diğerleri ise sabit tutulamaz (girişteki örneği hatırlayın: bu imkansız olurdu). " t i sabit tutmak " için ve aynı zamanda t i 2 ) değerini değiştirin .
Marjinal etki büyük olduğunda bile benzersiz etkinin neredeyse sıfır olması mümkündür. Bu ima olabileceğine dair bazı diğer eş değişken yakalar tüm bilgiler x j , böylece değişken modelinde bir kez, hiçbir katkısı olmadığı x j içinde varyasyona y . Tersine, marjinal etkisi neredeyse sıfır iken x j'nin benzersiz etkisi büyük olabilir. Bu, diğer ortak değişkenler y'nin varyasyonunun büyük bir kısmını açıklasaydı gerçekleşirdi , ancak esas olarak varyasyonu, x j tarafından yakalananları tamamlayıcı bir şekilde açıklarlar . Bu durumda, modele diğer değişkenleri dahil etmek, y'nin değişkenliğinin x j ile ilgisi olmayan kısmını azaltır , böylece x j ile görünen ilişkiyi güçlendirir .
"Sabit tutulan" ifadesinin anlamı, tahmin edici değişkenlerin değerlerinin nasıl ortaya çıktığına bağlı olabilir. Deneyi yapan kişi, bir çalışma tasarımına göre yordayıcı değişkenlerin değerlerini doğrudan ayarlarsa, ilgili karşılaştırmalar, tam anlamıyla, yordayıcı değişkenleri deneyci tarafından "sabit tutulan" birimler arasındaki karşılaştırmalara karşılık gelebilir. Alternatif olarak, "sabit tutulan" ifadesi, veri analizi bağlamında yer alan bir seçime atıfta bulunabilir. Bu durumda, verilen tahmin değişkeni için ortak bir değere sahip olan verilerin alt kümelerine dikkatimizi sınırlayarak "bir değişkeni sabit tutarız". Bu, gözlemsel bir çalışmada kullanılabilecek "sabit tutulan"ın tek yorumudur.
"Benzersiz etki" kavramı, birbiriyle ilişkili birden çok bileşenin yanıt değişkenini etkilediği karmaşık bir sistem üzerinde çalışırken çekicidir. Bazı durumlarda, bir yordayıcı değişkenin değeriyle bağlantılı bir müdahalenin nedensel etkisi olarak tam anlamıyla yorumlanabilir. Bununla birlikte, birçok durumda çoklu regresyon analizinin, tahmin ediciler birbiriyle ilişkili olduğunda ve bir çalışma tasarımına göre atanmadığında, tahmin edici değişkenler ile yanıt değişkeni arasındaki ilişkileri netleştirmede başarısız olduğu iddia edilmiştir.
Uzantılar
Temel modelin altında yatan varsayımların bir kısmının veya tamamının gevşetilmesine izin veren çok sayıda doğrusal regresyon uzantısı geliştirilmiştir.
Basit ve çoklu doğrusal regresyon

Tek bir skaler tahmin değişkeni x ve tek bir skaler yanıt değişkeni y'nin en basit durumu , basit doğrusal regresyon olarak bilinir . Birden fazla ve / veya uzatma vektörü (büyük ile gösterilir belirleyici değişkenlerin -valued X ) olarak bilinen , çoklu doğrusal regresyon olarak da bilinen, çok değişkenli doğrusal regresyon ile (karıştırılmamalıdır değişkenli doğrusal regresyon ).
Çoklu doğrusal regresyon, basit doğrusal regresyonun birden fazla bağımsız değişken durumuna genelleştirilmesi ve bir bağımlı değişkenle sınırlı genel doğrusal modellerin özel bir durumudur . Çoklu doğrusal regresyon için temel model,
her gözlem için i = 1, ... , n .
Yukarıdaki formülde , bir bağımlı değişkenin ve p bağımsız değişkenin n gözlemini ele alıyoruz . Bu durumda, Y, I olan I inci bağımlı değişken gözlenmesi, X ij olan I inci gözlenmesi j inci , bağımsız değişken j = 1, 2, ..., p . Değerlerin β j parametreleri verileri temsil ve e i olan i inci bağımsız aynen dağılma normal hata.
Daha genel çok değişkenli doğrusal regresyonda, aynı açıklayıcı değişkenler setini paylaşan ve dolayısıyla birbirleriyle eşzamanlı olarak tahmin edilen m > 1 bağımlı değişkenlerin her biri için yukarıdaki formun bir denklemi vardır :
i = 1, ... , n olarak indekslenen tüm gözlemler için ve j = 1, ... , m olarak indekslenen tüm bağımlı değişkenler için .
Neredeyse tüm gerçek dünya regresyon modelleri, çoklu tahmin edicileri içerir ve doğrusal regresyonun temel açıklamaları, genellikle çoklu regresyon modeli açısından ifade edilir. Ancak, bu durumlarda yanıt değişkeni y'nin hala bir skaler olduğuna dikkat edin. Diğer bir terim, çok değişkenli doğrusal regresyon , y'nin bir vektör olduğu, yani genel doğrusal regresyon ile aynı olduğu durumları ifade eder .
Genel doğrusal modeller
Genel lineer model yanıt değişkeni (her gözlem için) skalar olmayan durum ancak vektör, dikkate y ı . Klasik doğrusal regresyon modelinin β vektörünün yerini alan bir B matrisi ile koşullu doğrusallık hala varsayılmaktadır . Sıradan en küçük karelerin (OLS) ve genelleştirilmiş en küçük karelerin (GLS) çok değişkenli analogları geliştirilmiştir. "Genel doğrusal modeller", "çok değişkenli doğrusal modeller" olarak da adlandırılır. Bunlar, çok değişkenli doğrusal modeller ("çoklu doğrusal modeller" olarak da adlandırılır) ile aynı değildir.
Heteroskedastik modeller
Değişen varyansa izin veren çeşitli modeller oluşturulmuştur , yani farklı yanıt değişkenleri için hataların farklı varyansları olabilir . Örneğin, ağırlıklı en küçük kareler , yanıt değişkenlerinin muhtemelen ilişkili hatalarla farklı hata varyanslarına sahip olabileceği durumlarda doğrusal regresyon modellerini tahmin etmek için bir yöntemdir. (Ayrıca bkz. Ağırlıklı doğrusal en küçük kareler ve Genelleştirilmiş en küçük kareler .) Değişken varyansla tutarlı standart hatalar , ilişkisiz ancak potansiyel olarak değişen varyanslı hatalarla kullanım için geliştirilmiş bir yöntemdir.
Genelleştirilmiş doğrusal modeller
Genelleştirilmiş doğrusal modeller (GLM'ler), sınırlı veya ayrık olan yanıt değişkenlerini modellemek için bir çerçevedir. Bu kullanılır, örneğin:
- Log-normal dağılım veya Poisson dağılımı gibi çarpık bir dağılım kullanılarak daha iyi tanımlanmış olan (örneğin, fiyatlar veya popülasyonlar) büyük ölçekte değişen pozitif miktarları modellerken (GLM'ler log-normal veriler için kullanılmasa da, yanıt yerine değişken basitçe logaritma işlevi kullanılarak dönüştürülür);
- bir seçimde belirli bir adayın seçimi gibi kategorik verileri modellerken ( ikili seçimler için bir Bernoulli dağılımı / binom dağılımı veya çok yönlü seçimler için bir kategorik dağılım / çok terimli dağılım kullanılarak daha iyi tanımlanır ), burada bir anlamlı bir şekilde sıralanamayan sabit sayıda seçenek;
- sıralı verileri modellerken , örneğin 0 ile 5 arasında bir ölçekte derecelendirmeler, farklı sonuçların sıralanabileceği ancak miktarın kendisinin mutlak bir anlamı olmayabileceği (ör. 4 derecelendirmesi herhangi bir amaç için "iki kat daha iyi" olmayabilir) 2 puan olarak anlamlıdır, ancak 2 veya 3'ten daha iyi olduğunu ancak 5 kadar iyi olmadığını belirtir.
Genelleştirilmiş doğrusal modeller , yanıt değişken(ler)inin ortalamasını tahmin edicilerle ilişkilendiren keyfi bir bağlantı işlevine ( g) izin verir : . Bağlantı işlevi, genellikle yanıtın dağılımı ile ilgilidir ve özellikle, tipik olarak, doğrusal tahmin edicinin aralığı ile yanıt değişkeninin aralığı arasında dönüştürme etkisine sahiptir .
GLM'lerin bazı yaygın örnekleri şunlardır:
- Sayım verileri için Poisson regresyonu .
- İkili veriler için lojistik regresyon ve probit regresyon .
- Kategorik veriler için çok terimli lojistik regresyon ve çok terimli probit regresyon.
- Sıralı veriler için sıralı logit ve sıralı probit regresyonu.
Tek indeksli modeller , klasik lineer regresyon modelinde olduğu gibi lineer öngörücü β ′ x'in merkezi rolünü korurken, x ve y arasındaki ilişkide bir dereceye kadar doğrusal olmayanlığa izin verir . Belirli koşullar altında, tek endeksli bir modelden elde edilen verilere basitçe OLS uygulamak, orantılılık sabitine kadar tutarlı bir şekilde β tahmininde bulunacaktır .
Hiyerarşik doğrusal modeller
Hiyerarşik doğrusal modeller (veya çok düzeyli regresyon ), verileri bir gerileme hiyerarşisi halinde düzenler; örneğin, burada A , B üzerinde ve B , C üzerinde geri çekilir . İlgilenilen değişkenlerin doğal bir hiyerarşik yapıya sahip olduğu, örneğin eğitim istatistiklerinde, öğrencilerin sınıflarda iç içe olduğu, sınıfların okullarda iç içe olduğu ve okulların bir okul bölgesi gibi bazı idari gruplarda iç içe olduğu durumlarda sıklıkla kullanılır. Yanıt değişkeni, bir test puanı gibi öğrenci başarısının bir ölçüsü olabilir ve sınıf, okul ve okul bölgesi düzeylerinde farklı ortak değişkenler toplanabilir.
Değişkenlerdeki hatalar
Değişkenlerde hata modelleri (veya "ölçüm hatası modelleri"), geleneksel doğrusal regresyon modelini, X tahmin değişkenlerinin hatalı olarak gözlemlenmesine izin verecek şekilde genişletir . Bu hata, standart β tahmin edicilerinin sapmalı olmasına neden olur . Genel olarak, önyargı biçimi bir zayıflamadır, yani etkilerin sıfıra doğru eğilimli olduğu anlamına gelir.
Diğerleri
- Gelen Dempster-Shafer teori ya da bir doğrusal inanç işlevi , özellikle de, bir doğrusal regresyon modeli gözlemler ve diğer assumed normal dağılımlar ve durum denklemlerinin temsil benzer matrisler ile kombine edilebilir kısmen süpürüldü matris olarak temsil edilebilir. Süpürülmüş veya taranmamış matrislerin kombinasyonu, doğrusal regresyon modellerini tahmin etmek için alternatif bir yöntem sağlar.
Tahmin yöntemleri
Doğrusal regresyonda parametre tahmini ve çıkarım için çok sayıda prosedür geliştirilmiştir . Bu yöntemler, algoritmaların hesaplama basitliği, kapalı biçimli bir çözümün varlığı, ağır kuyruklu dağılımlara göre sağlamlık ve tutarlılık ve asimptotik verimlilik gibi arzu edilen istatistiksel özellikleri doğrulamak için gereken teorik varsayımlarda farklılık gösterir .
Doğrusal regresyon için daha yaygın tahmin tekniklerinden bazıları aşağıda özetlenmiştir.
Bağımsız değişkenin ve modelin parametrelerinin olduğunu varsayarsak , modelin tahmini şöyle olur:
- .
Eğer uzatılırsa, o zaman parametrenin ve bağımsız değişkenin bir nokta çarpımı olur, yani
- .
En küçük kareler ayarında, optimum parametre, ortalama kare kaybının toplamını en aza indirecek şekilde tanımlanır:
Şimdi bağımsız ve bağımlı değişkenleri matrislere koyarak ve sırasıyla kayıp fonksiyonu şu şekilde yeniden yazılabilir:
Kayıp dışbükey olduğundan optimum çözüm gradyan sıfırdadır. Kayıp fonksiyonunun gradyanı ( Payda düzeni kuralı kullanılarak ):
Gradyanı sıfıra ayarlamak optimum parametreyi üretir:
Not: Elde edilenin gerçekten de yerel minimum olduğunu kanıtlamak için, Hessian matrisini elde etmek için bir kez daha türev almalı ve bunun pozitif tanımlı olduğunu göstermelidir. Bu Gauss-Markov teoremi tarafından sağlanır .
Doğrusal en küçük kareler yöntemleri temel olarak şunları içerir:
- Hata terimlerinin dağılımının , olasılık dağılımlarının belirli bir ƒ θ parametrik ailesine ait olduğu bilindiğinde, maksimum olabilirlik tahmini yapılabilir. Tüm ön θ sıfır olan bir normal dağılım olup , ortalama ve varyans hesaplanmasıyla, elde edilen tahmin En Küçük Kareler tahmin etmek için aynıdır. GLS tahminleri, ε bilinen bir kovaryans matrisi ile çok değişkenli bir normal dağılımı takip ettiğinde maksimum olabilirlik tahminleridir.
- Ridge regresyonu ve Kement regresyonu gibi diğer cezalandırılmış tahmin biçimleri, tahminin değişkenliğini azaltmak içinkasıtlıolarak β tahminine önyargı ekler . Ortaya çıkan tahminler genellikleOLS tahminlerinden dahadüşük ortalama karesel hataya sahiptir, özellikle çoklu bağlantı mevcut olduğunda veya fazla uydurma bir sorun olduğunda. Genellikle amaç,henüz gözlemlenmemiş x tahmin edicilerinin değerleriiçin yanıt değişkeni y'nin değerini tahmin etmek olduğunda kullanılır. Bu yöntemler, yanlılığı hesaba katmak zor olduğundan, amaç çıkarsama olduğunda o kadar yaygın olarak kullanılmaz.
- En küçük mutlak sapma (LAD) regresyonu,aykırı değerlerin varlığına OLS'den daha az duyarlı olduğu için (ancak aykırı değer olmadığında OLS'den daha az verimli olduğu için) sağlam bir tahmin tekniğidir. ε içinbir Laplace dağılım modelialtında maksimum olabilirlik tahminine eşdeğerdir.
- Uyarlanabilir tahmin . Hata terimlerinin regresörlerden bağımsız olduğunu varsayarsak , o zaman optimal tahmin edici, ilk adımın hata teriminin dağılımını parametrik olmayan bir şekilde tahmin etmek için kullanıldığı 2 adımlı MLE'dir.
Diğer tahmin teknikleri

- Bayes doğrusal regresyon , Bayes istatistiklerinin çerçevesini doğrusal regresyona uygular. (Ayrıca bkz. Bayesian çok değişkenli doğrusal regresyon .) Özellikle, regresyon katsayıları β'nın önceden belirlenmiş bir dağılıma sahip rastgele değişkenler olduğu varsayılır. Önceki dağılım, sırt regresyonuna veya kement regresyonuna benzer (ancak daha genel) bir şekilde, regresyon katsayıları için çözümleri saptırabilir . Ek olarak, Bayesian tahmin süreci, regresyon katsayılarının "en iyi" değerleri için tek bir nokta tahmini değil, niceliği çevreleyen belirsizliği tamamen tanımlayantüm bir sonsal dağılım üretir. Bu ortalama, mod, medyan, herhangi quantile kullanarak "en iyi" katsayılarını tahmin etmek için kullanılabilir (bkz kuantil regresyon ) veya arka dağıtım başka işlevi.
- Dilim regresyon koşullu kuantiller odaklanır y verilen X yerine koşullu ortalama y verilen X . Doğrusal nicelik regresyon, belirli bir koşullu niceliği, örneğin koşullu medyanı,öngörücülerindoğrusal bir işlevi β T x olarak modeller.
- Karma modeller , bağımlılıklar bilinen bir yapıya sahip olduğunda, bağımlı verileri içeren doğrusal regresyon ilişkilerini analiz etmek için yaygın olarak kullanılır. Karma modellerin yaygın uygulamaları, boylamsal veriler veya küme örneklemesinden elde edilen veriler gibi tekrarlanan ölçümleri içeren verilerin analizini içerir. Genelliklemaksimum olabilirlik veya Bayes tahmini kullanan parametrik modellerolarak uygundurlar. Hataların normal rastgele değişkenlerolarak modellenmesi durumunda, karma modeller ile genelleştirilmiş en küçük kareler arasında yakın bir bağlantı vardır. Sabit etkiler tahmini , bu tür verileri analiz etmek için alternatif bir yaklaşımdır.
- Temel bileşen regresyonu (PCR), öngörücü değişkenlerin sayısı büyük olduğunda veya öngörücü değişkenler arasında güçlü korelasyonlar olduğunda kullanılır. Bu iki aşamalı prosedür, önce temel bileşen analizini kullanarak öngörücü değişkenleri azaltır,ardından bir OLS regresyon uyumunda indirgenmiş değişkenleri kullanır. Pratikte genellikle iyi çalışsa da, öngörücü değişkenlerin en bilgilendirici doğrusal fonksiyonunun, öngörücü değişkenlerin çok değişkenli dağılımının baskın temel bileşenleri arasında yer alması gerektiğine dair genel bir teorik neden yoktur. Kısmi en küçük kareler regresyon bahsedilen eksikliği muzdarip değildir PCR yönteminin bir uzantısıdır.
- En küçük açılı regresyon , potansiyel olarak gözlemlerden daha fazla ortak değişkenli yüksek boyutlu ortak değişken vektörlerini işlemek için geliştirilmiş doğrusal regresyon modelleri için bir tahmin prosedürüdür.
- Theil-Sen tahmin basit bir sağlam tahmini örnek nokta çiftleri ile hattın kaymalarının orta olmak için uygun çizgisinin eğimini seçer tekniği. Basit doğrusal regresyona benzer istatistiksel verimlilik özelliklerine sahiptir ancak aykırı değerlere karşı çok daha az duyarlıdır .
- α-kırpılmış ortalama yaklaşımı ve L-, M-, S- ve R-tahmin edicileri dahil olmak üzere diğer sağlam tahmin teknikleri tanıtıldı.
Uygulamalar
Doğrusal regresyon, biyolojik, davranışsal ve sosyal bilimlerde değişkenler arasındaki olası ilişkileri tanımlamak için yaygın olarak kullanılmaktadır. Bu disiplinlerde kullanılan en önemli araçlardan biri olarak yer almaktadır.
eğilim çizgisi
Bir eğilim hattı bir eğilim gösterir, uzun süreli hareket zaman serisi diğer bileşenler sonra veri muhasebeleştirilmişlerdir. Belirli bir veri setinin (örneğin GSYİH, petrol fiyatları veya hisse senedi fiyatları) zaman içinde arttığını veya azaldığını söyler. Bir eğilim çizgisi, bir dizi veri noktası aracılığıyla gözle kolayca çizilebilir, ancak konumları ve eğimleri, doğrusal regresyon gibi istatistiksel teknikler kullanılarak daha doğru bir şekilde hesaplanır. Trend çizgileri tipik olarak düz çizgilerdir, ancak bazı varyasyonlar çizgide istenen eğrilik derecesine bağlı olarak daha yüksek dereceli polinomlar kullanır.
Trend çizgileri, zaman içinde verilerdeki değişiklikleri göstermek için bazen iş analitiğinde kullanılır. Bunun basit olma avantajı vardır. Eğilim çizgileri genellikle belirli bir eylem veya olayın (eğitim veya reklam kampanyası gibi) belirli bir zamanda gözlemlenen değişikliklere neden olduğunu savunmak için kullanılır. Bu basit bir tekniktir ve bir kontrol grubu, deneysel tasarım veya karmaşık bir analiz tekniği gerektirmez. Bununla birlikte, diğer potansiyel değişikliklerin verileri etkileyebileceği durumlarda bilimsel geçerlilik eksikliğinden muzdariptir.
epidemiyoloji
Tütün içimini mortalite ve morbidite ile ilişkilendiren erken kanıtlar , regresyon analizini kullanan gözlemsel çalışmalardan geldi . Gözlemsel verileri analiz ederken sahte korelasyonları azaltmak için , araştırmacılar genellikle birincil ilgi değişkenine ek olarak regresyon modellerine birkaç değişken ekler. Örneğin, sigara içmenin birincil ilgi bağımsız değişkeni olduğu ve bağımlı değişkenin yıllarla ölçülen yaşam süresi olduğu bir regresyon modelinde, araştırmacılar, sigara içmenin yaşam süresi üzerinde gözlemlenen herhangi bir etkisinin olduğundan emin olmak için ek bağımsız değişkenler olarak eğitim ve geliri dahil edebilir. diğer sosyo-ekonomik faktörlerden dolayı değil . Bununla birlikte, ampirik bir analize tüm olası karıştırıcı değişkenleri dahil etmek asla mümkün değildir . Örneğin, varsayımsal bir gen, ölüm oranını artırabilir ve ayrıca insanların daha fazla sigara içmesine neden olabilir. Bu nedenle, randomize kontrollü araştırmalar , gözlemsel verilerin regresyon analizleri kullanılarak elde edilebilecek olandan daha fazla nedensel ilişkiler kanıtı üretebilir. Kontrollü deneyler mümkün olmadığında , gözlemsel verilerden nedensel ilişkileri tahmin etmeye çalışmak için araç değişkenler regresyonu gibi regresyon analizi varyantları kullanılabilir.
finans
Sermaye varlıkları fiyatlandırma modeli lineer regresyon yanı sıra kavramını kullanır beta analizi için ve bir yatırımın sistematik riskini hesaplamak. Bu, doğrudan, yatırım getirisini tüm riskli varlıkların getirisi ile ilişkilendiren doğrusal regresyon modelinin beta katsayısından gelir.
ekonomi
Doğrusal regresyon, ekonomide baskın ampirik araçtır . Örneğin, tahmin etmek için kullanılan tüketim harcamalarını , sabit yatırım harcamaları, envanter yatırımı , bir ülkenin alımları ihracatı , harcama ithalat , talep likit varlıklara sahip üzere , işgücü talebini ve emek arzını .
Çevre Bilimi
Doğrusal regresyon, çok çeşitli çevre bilimi uygulamalarında uygulama bulur. Kanada'da, Çevresel Etkileri İzleme Programı , kağıt hamuru değirmeni veya metal madeni atıklarının su ekosistemi üzerindeki etkilerini ölçmek için balık ve bentik araştırmalar üzerinde istatistiksel analizler kullanır .
Makine öğrenme
Doğrusal regresyon, yapay zekanın makine öğrenimi olarak bilinen alt alanında önemli bir rol oynamaktadır . Doğrusal regresyon algoritması, göreceli basitliği ve iyi bilinen özellikleri nedeniyle temel denetimli makine öğrenmesi algoritmalarından biridir.
Tarih
En küçük kareler doğrusal regresyonu, bir noktalar kümesine iyi bir kaba doğrusal uyum bulmanın bir yolu olarak, Legendre (1805) ve Gauss (1809) tarafından gezegen hareketinin tahmini için gerçekleştirilmiştir. Quetelet , prosedürün iyi bilinmesinden ve sosyal bilimlerde yaygın olarak kullanılmasından sorumluydu.
Ayrıca bakınız
- varyans analizi
- Blinder-Oaxaca ayrışması
- Sansürlü regresyon modeli
- Kesitsel regresyon
- Eğri uydurma
- Ampirik Bayes yöntemleri
- Hatalar ve artıklar
- Uygun olmayan kareler toplamı
- Hat uydurma
- Doğrusal sınıflandırıcı
- Doğrusal Denklem
- Lojistik regresyon
- M-tahmincisi
- Çok değişkenli uyarlanabilir regresyon spline'ları
- Doğrusal olmayan regresyon
- parametrik olmayan regresyon
- Normal denklemler
- Projeksiyon takip regresyonu
- Tepki modelleme metodolojisi
- Parçalı doğrusal regresyon
- kademeli regresyon
- yapısal kırılma
- Destek vektör makinesi
- Kesilmiş regresyon modeli
- Deming regresyonu
Referanslar
alıntılar
Kaynaklar
- Cohen, J., Cohen P., West, SG ve Aiken, LS (2003). Davranış bilimleri için uygulamalı çoklu regresyon/korelasyon analizi . (2. baskı) Hillsdale, NJ: Lawrence Erlbaum Associates
- Charles Darwin'in fotoğrafı . Evcilleştirme Altında Hayvan ve Bitkilerin Varyasyonu . (1868) (Bölüm XIII, Galton'un zamanında geri dönüş hakkında bilinenleri anlatır. Darwin, "geri dönüş" terimini kullanır.)
- Draper, NR; Smith, H. (1998). Uygulamalı Regresyon Analizi (3. baskı). John Wiley. ISBN'si 978-0-471-17082-2.
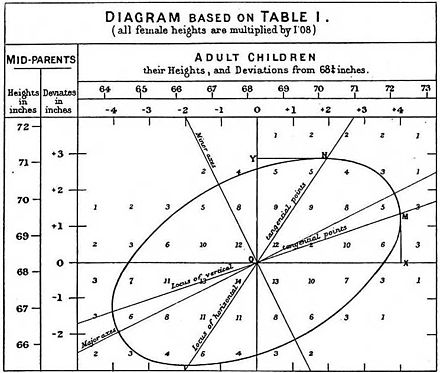
- Francis Galton. "Kalıtsal Boyda Sıradanlığa Doğru Gerileme," Antropoloji Enstitüsü Dergisi , 15:246-263 (1886). (Faks: [1] )
- Robert S. Pindyck ve Daniel L. Rubinfeld (1998, 4h ed.). Ekonometrik Modeller ve Ekonomik Tahminler , ch. 1 (Giriş, Σ operatörleri ve parametre tahmininin türetilmesi ile ilgili ekler dahil) & Ek 4.3 (matris formunda çoklu regresyon).
daha fazla okuma
- Pedhazur, Elazar J (1982). Davranış araştırmalarında çoklu regresyon: Açıklama ve tahmin (2. baskı). New York: Holt, Rinehart ve Winston. ISBN'si 978-0-03-041760-3.
- Mathieu Rouaud, 2013: Olasılık, İstatistik ve Tahmin Bölüm 2: Doğrusal Regresyon, Hata Çubuklarıyla Doğrusal Regresyon ve Doğrusal Olmayan Regresyon.
- Ulusal Fizik Laboratuvarı (1961). "Bölüm 1: Doğrusal Denklemler ve Matrisler: Doğrudan Yöntemler". Modern Hesaplama Yöntemleri . Uygulamalı Bilimler Üzerine Notlar. 16 (2. baskı). Majestelerinin Kırtasiye Ofisi .
Dış bağlantılar
- En Küçük Kareler Regresyonu , PhET Etkileşimli simülasyonlar, Boulder'daki Colorado Üniversitesi
- DIY Doğrusal Uyum






























![{\displaystyle {\vec {x_{i}}}=\sol[x_{1}^{i},x_{2}^{i},\ldots ,x_{m}^{i}\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/156ecace8a311d501c63ca49c73bba6efc915283)
![{\displaystyle {\vec {\beta }}=\sol[\beta _{0},\beta _{1},\ldots ,\beta _{m}\sağ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32434f0942d63c868f23d5af39442bb90783633b)


![{\displaystyle {\vec {x_{i}}}=\left[1,x_{1}^{i},x_{2}^{i},\ldots ,x_{m}^{i}\right ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72fa7acd1682497c285884b0686d784d8b0eb15)








