Pons asinorum -Pons asinorum

Byrne'nin Elementler baskısındaki pons asinorum , Öklid'in kanıtının bir bölümünü gösterir.

İn geometrisi , deyim açıları bir eşit iki zıt ikizkenar üçgen kendileri olarak bilinen eşit olan pons asinorum ( : Latin  [konum asɪnoːrũː] , İngilizce: / p ɒ n z ˌ æ s ɪ N ɔːr ə m / PONZ ass-i- NOR -əm ), tipik olarak " kıç köprüsü" olarak çevrilir . Bu ifade içinde 1. Kitap Önerme 5'tir Öklid 'in Elements ve olarak da bilinir ikizkenar üçgen teoremi . Bunun tersi de doğrudur: Bir üçgenin iki açısı eşitse, karşılarındaki kenarlar da eşittir. Terim aynı zamanda Pisagor teoremine de uygulanır .

Pons asinorum , aynı zamanda, yetenekli ve yetersiz akıl yürütücüleri ayıran bir alanda eleştirel düşünmenin bir testi olarak hareket eden bir problem veya meydan okuma için mecazi olarak kullanılır; bir yetenek veya anlayış testini temsil eder. Bu konuda bilinen ilk kullanımı 1645'teydi.

Kalıcı bir matematiksel folklor parçası, bir yapay zeka programının bu teoremin orijinal ve daha zarif bir kanıtını keşfettiğini iddia ediyor . Aslında, Marvin Minsky , (farkında olmadığı) Pappus kanıtını mekanik bir teorem kanıtlayıcısının yapabileceklerini simüle ederek yeniden keşfettiğini anlatıyor .

Kanıtlar

Proclus'un kanıtı

Öklid'in Elementler Kitabı 1, önerme 5; pons asinorum

Öklid ve Proclus

Euclid'in pons asinorum ifadesi, üçgenin eşit kenarları tabanın altına uzatılırsa, uzantılar ve taban arasındaki açıların da eşit olduğu şeklindeki ikinci bir sonucu içerir. Öklid'in ispatı , bu uzantılara yardımcı çizgiler çizmeyi içerir. Ancak, Euclid'in yorumcusu Proclus'un işaret ettiği gibi, Euclid asla ikinci sonucu kullanmaz ve ispatı, bunun yerine yardımcı çizgiler üçgenin kenarlarına çekilerek bir şekilde basitleştirilebilir, ispatın geri kalanı aşağı yukarı aynı şekilde ilerler.

Öklid'in ispatı daha karmaşık hale getirdiği göz önüne alındığında, neden teoreme ikinci sonucu eklediğine dair çok fazla spekülasyon ve tartışma olmuştur. Proclus tarafından verilen makul bir açıklama, ikinci sonucun Öklid'in her durumu kapsamadığı sonraki önermelerin kanıtlarına olası itirazlarda kullanılabileceğidir. Kanıt, büyük ölçüde, bugün yan-açı-yan olarak adlandırılan , Elementler'deki önceki önermeye dayanır .

Euclid'in ispatının Proclus' varyasyonu aşağıdaki gibi ilerler:

Let ABC bir ikizkenar üçgen olması AB ve AC eşit tarafı olmak. İsteğe bağlı bir nokta al D tarafında AB ve yapı E ile AC böylece AD  =  AE . BE , DC ve DE çizgilerini çizin .

BAE ve CAD üçgenlerini düşünün ; BA  =  CA , AE  =  AD ve kendisine eşittir, yani yan-açı-yan olarak, üçgenler eştir ve karşılık gelen kenarlar ve açılar eşittir.${\görüntüleme stili \açı A}$

Bu nedenle ve ve BE  =  CD .${\displaystyle \açı ABE=\açı ACD}$${\displaystyle \açı ADC=\açı AEB}$

Yana AB  =  AC ve AD  =  AE , BD  =  CE eşit parçalarının çıkarılması ile.

Şimdi DBE ve ECD üçgenlerini düşünün ; BD  =  CE , BE  =  CD ve az önce gösterildi, bu nedenle tekrar yan-açı-yan uygulandığında, üçgenler uyumludur.${\displaystyle \açı DBE=\açı ECD}$

Bu nedenle ve .${\görüntüleme stili \açı BDE=\CED açısı}$${\displaystyle \angle BED=\angle CDE}$

Ber ve , eşit parçaların çıkarılmasıyla.${\görüntüleme stili \açı BDE=\CED açısı}$${\displaystyle \açı CDE=\açı YATAK}$${\görüntüleme stili \açı BDC=\açı CEB}$

Üçüncü bir üçgen çifti düşünün, BDC ve CEB ; DB  =  EC , DC  =  EB ve böylece yan açı-yan üçüncü kez uygulandığında üçgenler uyumludur.${\görüntüleme stili \açı BDC=\açı CEB}$

Özellikle, kanıtlanması gereken CBD  =  BCE açısı .

Pappus

Proclus , İskenderiyeli Pappus'a atfedilen çok daha kısa bir kanıt verir . Bu sadece daha basit olmakla kalmaz, aynı zamanda hiçbir ek inşaat gerektirmez. İspat yöntemi, üçgene ve onun ayna görüntüsüne yan-açı-yan uygulamaktır. Daha modern yazarlar, önceki önerme için verilen ispat yöntemini taklit ederek bunu üçgeni almak, ters çevirmek ve kendi üzerine yerleştirmek olarak tanımlamışlardır. Bu yöntem Charles Lutwidge Dodgson tarafından Euclid ve Modern Rakipleri'nde hicvedildi ve buna " İrlandalı boğa " adı verildi, çünkü görünüşe göre üçgenin aynı anda iki yerde olmasını gerektiriyor.

Kanıt aşağıdaki gibidir:

Let ABC bir ikizkenar üçgen olması AB ve AC eşit tarafı olmak.

ABC ve ACB üçgenlerini düşünün; burada ACB , orijinal üçgende A , C ve B köşeleri sırasıyla A , B ve C'ye karşılık gelen ikinci bir üçgen olarak kabul edilir .

${\görüntüleme stili \açı A}$kendisine eşittir, AB  =  AC ve AC  =  AB , yani yan açı-yan açısından ABC ve ACB üçgenleri eştir.

Özellikle, .${\görüntüleme stili \açı B=\açı C}$

Diğerleri

Bir ders kitabı kanıtı

Standart bir ders kitabı yöntemi, A'daki açının açıortayını oluşturmaktır . Bu, Öklid'in ispatından daha basittir, ancak Öklid, 9. önermeye kadar bir açıortay yapımını sunmaz. Dolayısıyla, Öklid'in önermelerinin sunum sırası, dairesel akıl yürütme olasılığından kaçınmak için değiştirilmelidir.

Kanıt şu şekilde ilerler:

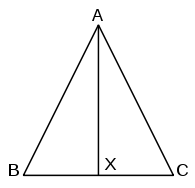
Daha önce olduğu gibi, üçgen olalım ABC ile AB  =  AC .

Açısı açıortay ve buluştuğu kadar uzatmak M.Ö. de X .${\görüntüleme stili \açı BAC}$

AB  =  AC ve AX kendisine eşittir.

Ayrıca, yan-açı-yan uygulandığında, BAX üçgeni ve CAX üçgeni uyumludur.${\displaystyle \angle BAX=\angle CAX}$

B ve C açılarının eşit olduğu sonucu çıkar.

Legendre , Éléments de géométrie'de benzer bir yapı kullanır , ancak X'i BC'nin orta noktası olarak alır . Kanıt benzerdir, ancak yan- açı-yan yerine yan-yan-yan kullanılmalıdır ve yan-yan-yan, Öklid tarafından Elements'in ilerleyen kısımlarına kadar verilmemiştir .

İç çarpım boşluklarında

İkizkenar üçgen teoremi , gerçek veya karmaşık sayılar üzerinde iç çarpım uzaylarında tutar . Bu tür alanlarda, bu vektörler diyor şeklini alır x , y ve z , eğer

${\displaystyle x+y+z=0{\metin{ ve }}\|x\|=\|y\|,}$

sonra

${\displaystyle \|xz\|=\|yz\|.}$

Dan beri

${\displaystyle \|xz\|^{2}=\|x\|^{2}-2x\cdot z+\|z\|^{2},}$

ve

${\displaystyle x\cdot z=\|x\|\|z\|\cos \theta }$

burada θ iki vektör arasındaki açı, teoremi bu iç çarpım alanı şeklinde sonuç açılarının eşitliği tablosuna karşılık gelir.

Etimoloji ve ilgili terimler

Ponsta için bir başka ortaçağ terim asinorum oldu Elefuga göre Roger Bacon , Yunan geliyor elegia "sefalet", ve Latin fuga "garibanlar uçuş" dir "uçuş". Bu etimoloji şüpheli olsa da, Chaucer'ın teorem için "yaban cıvıltıları" terimini kullanmasında yankılanır .

pons asinorum adının iki olası açıklaması vardır , en basiti kullanılan diyagramın gerçek bir köprüye benzemesidir. Ancak daha popüler açıklama, okuyucunun zekasının Unsurlarındaki ilk gerçek test olduğu ve takip eden daha zor önermelere bir "köprü" işlevi gördüğüdür. Gauss , bir zamanlar , birinci sınıf bir matematikçi olmak için bir ölçüt olarak Euler'in kimliğini hemen anlamanın gerekliliğine benzer bir inancı benimsemişti .

Benzer şekilde, adı Dulcarnon daha iyi olarak bilinen Öklid Kitabı I, 47. önerme verildi Pisagor teoremi Arapça sonra, Zülkarneyn DHU 'l ذو ٱلقرنين, 'iki boynuzu sahibini' anlamına teoremin diyagramlar gösterdi çünkü şeklin üst kısmında boynuz gibi iki küçük kare. Terim aynı zamanda bir ikilem için bir metafor olarak kullanılır. Teorem, bazen benzer nedenlerle "yel değirmeni" olarak da adlandırıldı.

mecazi kullanım

Eleştirel düşünme testi için bir metafor olarak pons asinorum'un kullanımları şunları içerir:

• Richard Aungerville'in Philobiblon'u, sarp bir uçurumu karşılaştıran "Quot Euclidis discipulos retrojecit Elefuga quasi scopulos eminens et abruptus, qui nullo scalarum suffragio scandi posset! Durus, inquiunt, est onun sermo; quis potest eum audire theore mi?" pasajını içerir. hiçbir merdivenin ölçeklemeye yardımcı olamayacağını ve kaç tane olası geometrinin geri çevrildiğini sorar.
• Vadeli pons asinorum , bir köprü hem de bir test olarak hem anlamı dahilinde, bir orta vadeli bulmak için bir metafor olarak kullanılır tasım .
• 18. yüzyıl şairi Thomas Campbell , "Pons asinorum" adlı mizahi bir şiir yazdı; burada bir geometri sınıfı, bir asker bölüğünün bir kaleyi ele geçirmesi gibi teoreme saldırır; savaş kayıpsız değildi.
• Ekonomist John Stuart Mill adında Ricardo'nun Kiralık Yasası'nı pons asinorum ekonomi.
• Pons Asinorum , bir Rubik Küpünün belirli bir konfigürasyonuna verilen addır .
• Eric Raymond , Python programlama dilinde sözdizimsel olarak anlamlı boşluk sorununa pons asinorum olarak atıfta bulundu.
• Fin aasinsilta ve İsveçli åsnebrygga neredeyse ama pek bir iki argüman veya konular arasında zayıf, hatta yapmacık bağlantısı, bir edebi tekniktir ilgisiz sonuç , aralarında garip bir geçiş olarak kullanılır. Ciddi metinlerde, bilinç akışına -ya da nedensel- tarzı yazıya tam olarak ait olduğu için, bu bir üslup hatası olarak kabul edilir . Tipik örnekler, konuların neden bağlantılı olduğunu açıklama zahmetine girmeden bir sonraki bölümün ne hakkında olduğunu söyleyerek bir bölümü bitirmek, rastgele bir sözü ayrıntılı bir işlemeye dönüştürmek veya konular arasında yapmacık bir bağlantı bulmaktır (örneğin, "Biraz kırmızı şarap aldık" ; kırmızı sıvılardan bahsetmişken, yarın Dünya Kan Bağışçısı Günü").
• In Hollandalı , ezelsbruggetje (kıçından küçük bir köprü ') bir kelime olduğunu anımsatıcı . Aynısı Alman Eselsbrücke için de geçerlidir .
• In Çek , oslí Mustek iki anlamı vardır - iki konu veya bir anımsatıcı arasındaki yapmacık bir bağlantı ya açıklayabilirsiniz.

Referanslar

Dış bağlantılar

• Pons asinorum , PlanetMath'te .
• DE Joyce'un Öklid'in Elementleri sunumu