Aritmetik hiyerarşi - Arithmetical hierarchy

Hiyerarşi seviyelerinin nasıl etkileşime girdiğine ve bazı temel küme kategorilerinin bunun içinde nerede bulunduğuna dair bir örnek.

Olarak matematiksel mantık , aritmetik hiyerarşi , aritmetik hiyerarşi ya da Kleene-Mostowski hiyerarşi (matematikçiler sonra Stephen Cole Kleene ve Andrzej Mostowski ), belirli sınıflandırır setleri göre karmaşıklığı tanımlandıkları formülleri. Bir sınıflandırma alan herhangi bir kümeye aritmetik denir .

Aritmetik hiyerarşi, özyineleme teorisinde , etkili tanımlayıcı küme teorisinde ve Peano aritmetiği gibi resmi teorilerin incelenmesinde önemlidir .

Tarski-Kuratowski algoritması üst bir formül ve tanımlar set tahsis sınıflandırmalar üzerine bağlanmış bir almak için kolay bir yol sağlar.

Hyperarithmetical hiyerarşi ve analitik hiyerarşi sınıfladıkları'nı ek formüller ve kümelerine aritmetik hiyerarşi uzatın.

Formüllerin aritmetik hiyerarşisi

Aritmetik hiyerarşi, birinci dereceden aritmetik dilindeki formüllere sınıflandırmalar atar . Sınıflandırmalar belirtilir ve doğal sayılar için n (0 dahil). Buradaki Yunan harfleri , formüllerin ayarlanmış parametreler içermediğini gösteren açık renkli sembollerdir. ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

Bir formül varsa sadece bir formüle mantıksal olarak eşdeğerdir sınırlandırılmış Nicelik sonra sınıflandırmaları atanır ve . ${\görüntüleme stili\phi }$${\görüntüleme stili\phi }$${\görüntüleme stili \Sigma _{0}^{0}}$${\displaystyle \Pi _{0}^{0}}$

Sınıflandırmalar ve aşağıdaki kurallar kullanılarak her doğal sayı n için tümevarımsal olarak tanımlanır : ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

• Eğer formun bir formül mantıksal olarak eşdeğerdir , olduğu , daha sonra sınıflandırma atanır .${\görüntüleme stili\phi }$${\displaystyle \var m_{1}\vardır m_{2}\cdots \vardır m_{k}\psi }$${\görüntüleme stili\psi }$${\displaystyle \Pi _{n}^{0}}$${\görüntüleme stili\phi }$${\displaystyle \Sigma _{n+1}^{0}}$
• Eğer formun bir formül mantıksal olarak eşdeğerdir , olduğu , daha sonra sınıflandırma atanır .${\görüntüleme stili\phi }$${\displaystyle \forall m_{1}\forall m_{2}\cdots \forall m_{k}\psi }$${\görüntüleme stili\psi }$${\displaystyle \Sigma _{n}^{0}}$${\görüntüleme stili\phi }$${\displaystyle \Pi _{n+1}^{0}}$

Bir formül, bazı varoluşsal niceleyicilerle başlayan ve varoluşsal ve evrensel niceleyiciler dizisi arasında zamanları dönüşümlü olarak değiştiren bir formüle eşdeğerdir ; Bir süre , formül bir formüle eşdeğerdir benzer şekilde bazı evrensel Nicelik ve alternatifleri ile başlar. ${\displaystyle \Sigma _{n}^{0}}$${\görüntüleme stili n-1}$${\displaystyle \Pi _{n}^{0}}$

Her birinci dereceden formülün bir ön ek normal formu olduğundan , her formüle en az bir sınıflandırma atanır. Fazla niceleyiciler herhangi bir formüle eklenebildiğinden, bir formül bir kez sınıflandırmaya atandığında veya ona sınıflandırmalar atanacaktır ve her r > n için . Bir formüle atanan tek ilgili sınıflandırma bu nedenle en az n'ye sahip olandır ; diğer tüm sınıflandırmalar ondan belirlenebilir. ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{r}^{0}}$${\displaystyle \Pi _{r}^{0}}$

Doğal sayı kümelerinin aritmetik hiyerarşisi

Doğal sayılar kümesi X , Peano aritmetiği dilinde formül φ ile tanımlanır (sıfır için "0", ardıl işlev için "S", toplama için "+", çarpma için "×" sembolleriyle birinci dereceden dil ve eşitlik için "="), X'in öğeleri tam olarak φ'yi sağlayan sayılarsa. Yani, tüm doğal sayılar için n ,

${\displaystyle n\in X\Leftrightarrow \mathbb {N} \models \varphi ({\underline {n}}),}$

aritmetik dilinde karşılık gelen sayı nerede . Bir küme, Peano aritmetiği dilinde bir formülle tanımlanmışsa, birinci mertebeden aritmetikte tanımlanabilir. ${\görüntüleme stili {\altı çizili {n}}}$${\görüntüleme stili n}$

Birinci mertebeden aritmetikte tanımlanabilen her X doğal sayı kümesine , doğal sayı olduğu yerde , , ve biçiminde sınıflandırmalar atanır . Eğer X, bir tanımlanabilen bir formül sonra X, sınıflandırma tayin edilir . Eğer X, bir tanımlanabilen bir formül sonra X, sınıflandırma tayin edilir . Eğer X hem de ve daha sonra ek sınıflandırma atanır . ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\görüntüleme stili n}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\görüntüleme stili X}$${\displaystyle \Delta _{n}^{0}}$

Formüllerden bahsetmenin nadiren mantıklı olduğuna dikkat edin ; bir formülün ilk niceleyicisi ya varoluşsaldır ya da evrenseldir. Yani bir küme bir formülle tanımlanmaz ; bunun yerine, hem de vardır ve kümesini tanımlamak formülleri. Örneğin, tek doğal sayılar kümesi ya veya ile tanımlanabilir . ${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\görüntüleme stili n}$${\displaystyle \forall k(n\neq 2\times k)}$${\displaystyle \var k(n=2\times k+1)}$

Doğal sayılar kümesinin sonlu Kartezyen güçleri üzerindeki aritmetik hiyerarşiyi tanımlamak için paralel bir tanım kullanılır . Bir serbest değişkenli formüller yerine, k - doğal sayı demetleri kümelerinde aritmetik hiyerarşiyi tanımlamak için k serbest sayı değişkenli formüller kullanılır . Bunlar aslında bir eşleştirme işlevinin kullanımıyla ilişkilidir .

Göreceli aritmetik hiyerarşiler

Biz kümesi için ne anlama geldiğini tanımlayabilir gibi X'in olmak özyinelemeli başka setine göre Y tanımlayan hesaplama izin vererek X danışmak Y biz bütün aritmetik hiyerarşiye bu kavramı genişletmek ve için ne anlama geldiğini tanımlayabilir bir kahin olarak X için olması , ya da içerisinde Y'nin , sırasıyla gösterilen ve . Bunu yapmak için, bir dizi Y tamsayısını düzeltin ve Peano aritmetiğinin diline Y'ye üyelik için bir yüklem ekleyin . Daha sonra söylemek X'in ise bir tarafından tanımlanır eğer bu genişletilmiş dilde formülü. Başka bir deyişle, X , Y'ye üyelik hakkında soru sormaya izin verilen bir formülle tanımlanmışsadır . Alternatif bir görüntüleyebilir setleri içinde özyinelemeli ile başlayan inşa edilebilir kümelerine olarak setleri Y ve dönüşümlü alarak sendikaları ve kavşakları kadar bu setleri n defa. ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$ ${\displaystyle \Delta _{n}^{0,Y}}$${\displaystyle \Pi _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$

Örneğin, Y bir tam sayı kümesi olsun. Let X'in O, Y'nin bir eleman tarafından bölünebilen sayıların kümesi X , aşağıdaki formül ile tanımlandığı böylece X olduğu (aslında içinde n sayısının her iki nicelik bağlanmış olabilir iyi yana gibi). ${\displaystyle \phi (n)=\vardır m\vardır t(Y(m)\land m\times t=n)}$${\görüntüleme stili \Sigma _{1}^{0,Y}}$${\displaystyle \Delta _{0}^{0,Y}}$

Aritmetik indirgenebilirlik ve dereceler

Aritmetik indirgenebilirlik, Turing indirgenebilirliği ile hiperaritmetik indirgenebilirlik arasında bir ara kavramdır .

Bir küme, Peano aritmetiği dilinde bir formülle tanımlanmışsa , aritmetiktir (ayrıca aritmetik ve aritmetik olarak tanımlanabilir ). Eşdeğer bir X eğer aritmetik olduğu X, bir ya da bir tam sayı için n . Bir dizi X, aritmetik olan bir dizi , Y , belirtilen eğer X, Peano aritmetik dilinde bir formül üyelik için bir dayanak tarafından uzatılan tanımlanabilir olduğunu Y . Aynı şekilde, X'in aritmetik bir Y ise X, içinde ya da bir tam sayı için n . Eşanlamlısı şudur: X , aritmetik olarak Y'ye indirgenebilir . ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$ ${\displaystyle X\leq _{A}Y}$${\displaystyle \Sigma _{n}^{0,Y}}$${\displaystyle \Pi _{n}^{0,Y}}$${\displaystyle X\leq _{A}Y}$

İlişki dönüşlü ve geçişlidir ve dolayısıyla kural tarafından tanımlanan ilişki${\displaystyle X\leq _{A}Y}$${\displaystyle \eşdeğer _{A}}$

${\displaystyle X\equiv _{A}Y\Leftrightarrow X\leq _{A}Y\land Y\leq _{A}X}$

denklik bağıntısıdır. Bu ilişkinin denklik sınıflarına aritmetik dereceler denir ; kısmen altında sıralanırlar . ${\displaystyle \leq _{A}}$

Cantor ve Baire uzayının alt kümelerinin aritmetik hiyerarşisi

Cantor alanı ile gösterilen , 0 ve 1 arasında her sonsuz dizilerin grubu olduğu; Baire boşluk , gösterilen veya doğal sayılar her sonsuz dizilerin bir kümesidir. Cantor uzayının elemanlarının tamsayı kümeleri ile ve Baire uzayının elemanları ile tam sayılardan tam sayılara kadar fonksiyonlarla tanımlanabileceğini unutmayın. ${\ Displaystyle 2^{\omega }}$${\görüntüleme stili \omega ^{\omega }}$${\görüntüleme stili {\matematiksel {N}}}$

İkinci mertebeden aritmetiğin olağan aksiyomizasyonu , küme niceleyicilerinin doğal olarak Cantor uzayı üzerinde niceleme olarak görülebildiği küme tabanlı bir dil kullanır. Bir formülle tanımlanabiliyorsa , Cantor uzayının bir alt kümesine sınıflandırma atanır . Bir formülle tanımlanabiliyorsa , kümeye sınıflandırma atanır . Küme her ikisi ise ve o zaman ek sınıflandırma verilir . Örneğin, tümü 0 olmayan tüm sonsuz ikili dizelerin kümesi olsun (veya eşdeğer olarak boş olmayan tüm tamsayı kümelerinin kümesi). Gördüğümüz gibi bu bir formülle tanımlanır ve dolayısıyla bir kümedir. ${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\ Displaystyle O\subset 2^{\omega }}$${\displaystyle O=\{X\in 2^{\omega }|\vardır n(X(n)=1)\}}$${\görüntüleme stili O}$${\görüntüleme stili \Sigma _{1}^{0}}$${\görüntüleme stili \Sigma _{1}^{0}}$

Cantor uzayının hem öğeleri (tamsayı kümeleri olarak kabul edilir) hem de Cantor uzayının alt kümeleri aritmetik hiyerarşilerde sınıflandırılırken, bunların aynı hiyerarşi olmadığını unutmayın. Aslında iki hiyerarşi arasındaki ilişki ilginçtir ve önemsiz değildir. Örneğin , Cantor uzayının elemanları (genel olarak) Cantor uzayının elemanları ile aynı değildir, yani bu Cantor uzayının bir alt kümesidir. Bununla birlikte, birçok ilginç sonuç iki hiyerarşiyi ilişkilendirir. ${\displaystyle \Pi _{n}^{0}}$${\görüntüleme stili X}$${\görüntüleme stili \{X\}}$${\displaystyle \Pi _{n}^{0}}$

Baire uzayının bir alt kümesinin aritmetik hiyerarşide sınıflandırılmasının iki yolu vardır.

• Baire alan bir alt-kümesi, her fonksiyon alan haritası altında Cantor alan karşılık gelen bir alt kümesi için için karakteristik fonksiyonu olarak grafik. Baire uzayının bir alt kümesine , , veya sadece ve ancak Cantor uzayının karşılık gelen alt kümesi aynı sınıflandırmaya sahipse, sınıflandırma verilir.${\görüntüleme stili\omega }$${\görüntüleme stili\omega }$${\displaystyle \Sigma _{n}^{1}}$${\displaystyle \Pi _{n}^{1}}$${\displaystyle \Delta _{n}^{1}}$
• Baire uzayındaki analitik hiyerarşinin eşdeğer bir tanımı, ikinci dereceden aritmetiğin işlevsel bir versiyonunu kullanarak formüllerin analitik hiyerarşisini tanımlayarak verilir; daha sonra Cantor uzayının alt kümeleri üzerindeki analitik hiyerarşi, Baire uzayındaki hiyerarşiden tanımlanabilir. Bu alternatif tanım, ilk tanımla tam olarak aynı sınıflandırmaları verir.

Baire uzayının veya Cantor uzayının sonlu Kartezyen güçleri üzerinde aritmetik hiyerarşiyi tanımlamak için birkaç serbest değişkenli formüller kullanarak paralel bir tanım kullanılır. Aritmetik hiyerarşi, herhangi bir etkin Polonya uzayında tanımlanabilir ; Cantor uzayı ve Baire uzayı için tanım özellikle basittir çünkü bunlar sıradan ikinci dereceden aritmetik diline uygundur.

Bazı tamsayılara göre Cantor ve Baire uzaylarının alt kümelerinin aritmetik hiyerarşisini de tanımlayabileceğimize dikkat edin. Aslında kalın yazı , yalnızca tüm tamsayı kümeleri için Y birleşimidir . Kalın karakter hiyerarşisinin yalnızca Borel kümelerinin standart hiyerarşisi olduğuna dikkat edin . ${\displaystyle \mathbf {\Sigma } _{n}^{0}}$${\displaystyle \Sigma _{n}^{0,Y}}$

Uzantılar ve varyasyonlar

Her ilkel özyinelemeli işlev için bir işlev simgesiyle genişletilmiş bir dil kullanarak formüllerin aritmetik hiyerarşisini tanımlamak mümkündür . Birinci mertebeden Peano aritmetiğinde ilkel özyinelemeli işlevlerin kullanılması , genel olarak, sınırsız bir varoluşsal niceleyici gerektirdiğinden ve dolayısıyla bu tanımda yer alan bazı kümeler, bu tanımın başında verilen tanımda yer aldığından , bu varyasyon, sınıflandırmasını biraz değiştirir. makale. ve böylece hiyerarşideki tüm üst sınıflar etkilenmeden kalır. ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\görüntüleme stili \Sigma _{0}^{0}}$${\görüntüleme stili \Sigma _{1}^{0}}$${\görüntüleme stili \Sigma _{1}^{0}}$

Doğal sayılar üzerindeki tüm sonlu ilişkilerde hiyerarşinin daha semantik bir varyasyonu tanımlanabilir; aşağıdaki tanım kullanılır. Her hesaplanabilir ilişki olarak tanımlanır . Sınıflandırmalar ve aşağıdaki kurallarla tümevarımsal olarak tanımlanmıştır. ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

• İlişki ise , ilişki şu şekilde tanımlanır:${\displaystyle R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle S(n_{1},\ldots ,n_{l})=\forall m_{1}\cdots \forall m_{k}R(n_{1},\ldots ,n_{l},m_{ 1},\ldots ,m_{k})}$${\displaystyle \Pi _{n+1}^{0}}$
• İlişki ise , ilişki şu şekilde tanımlanır:${\displaystyle R(n_{1},\ldots ,n_{l},m_{1},\ldots ,m_{k})\,}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle S(n_{1},\ldots ,n_{l})=\m_{1}\cdots \var m_{k}R(n_{1},\ldots ,n_{l},m_{ var) 1},\ldots ,m_{k})}$${\displaystyle \Sigma _{n+1}^{0}}$

Bu varyasyon, bazı kümelerin sınıflandırmasını biraz değiştirir. Özellikle, bir kümeler sınıfı olarak (sınıftaki ilişkiler tarafından tanımlanabilir), daha önce tanımlandığı şekliyle aynıdır . Doğal sayılar, Baire uzayı ve Cantor uzayı üzerindeki sonlu bağıntıları kapsayacak şekilde genişletilebilir. ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \Delta _{1}^{0}}$

gösterimin anlamı

Formüllerdeki aritmetik hiyerarşinin gösterimine aşağıdaki anlamlar eklenebilir.

Sembollerdeki alt simge ve bir formülde kullanılan evrensel ve varoluşsal sayı niceleyicilerinin bloklarının değişim sayısını gösterir. Ayrıca, en dıştaki blok formüllerde varoluşsal ve formüllerde evrenseldir . ${\görüntüleme stili n}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$

, , ve sembollerindeki üst simge , üzerinden nicelenen nesnelerin türünü belirtir. 0 türü nesneler doğal sayılardır ve tür nesneleri, türdeki nesneler kümesini doğal sayılarla eşleyen işlevlerdir . Doğal sayılardan doğal sayılara kadar olan işlevler gibi daha yüksek türdeki nesneler üzerinde niceleme, analitik hiyerarşide olduğu gibi 0'dan büyük bir üst simge ile tanımlanır . Üst simge 0, sayılar üzerinden niceleyicileri belirtir, üst simge 1, sayılardan sayılara (tip 1 nesneler) ilişkin nicelemeyi belirtir, üst simge 2, tip 1 nesnesi alan ve bir sayı döndüren işlevler üzerindeki nicelemeye karşılık gelir, vb. ${\görüntüleme stili 0}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\ Displaystyle i+1}$${\görüntüleme stili ben}$

Örnekler

• Sayılar kümesi biçimde bir formül ile tanımlanabilir olanlardır sadece sınırlı nicelik sahiptir. Bunlar tam olarak yinelemeli olarak numaralandırılabilen kümelerdir .${\görüntüleme stili \Sigma _{1}^{0}}$${\displaystyle \vardır n_{1}\cdots \vardır n_{k}\psi (n_{1},\ldots ,n_{k},m)}$${\görüntüleme stili\psi }$
• Toplam fonksiyonları hesaplayan Turing makineleri için indeks olan doğal sayılar kümesidir . Sezgisel olarak, bir dizin bu kümeye girer, ancak ve ancak her " dizinli Turing makinesinin adımlardan sonra girişte durduğu bir durum varsa ". Tam bir kanıt, önceki cümlede tırnak içinde görüntülenen özelliğin şu şekilde tanımlanabilir olduğunu gösterecektir. bir formülle Peano aritmetiğinin dili .${\displaystyle \Pi _{2}^{0}}$${\görüntüleme stili e}$${\görüntüleme stili m}$${\görüntüleme stili s}$${\görüntüleme stili e}$${\görüntüleme stili m}$${\görüntüleme stili s}$${\görüntüleme stili \Sigma _{1}^{0}}$
• Baire uzayının veya Cantor uzayının her alt kümesi, uzaydaki olağan topolojide bir açık kümedir. Ayrıca, böyle bir küme için, birleşimi orijinal küme olan temel açık kümelerin Gödel sayılarının hesaplanabilir bir numaralandırması vardır. Bu nedenle, kümeler bazen etkin olarak açık olarak adlandırılır . Benzer şekilde, her küme kapalıdır ve kümeler bazen etkin olarak kapalı olarak adlandırılır .${\görüntüleme stili \Sigma _{1}^{0}}$${\görüntüleme stili \Sigma _{1}^{0}}$${\görüntüleme stili \Pi _{1}^{0}}$${\görüntüleme stili \Pi _{1}^{0}}$
• Cantor uzayının veya Baire uzayının her aritmetik alt kümesi bir Borel kümesidir . Lightface Borel hiyerarşisi, aritmetik hiyerarşiyi ek Borel kümelerini içerecek şekilde genişletir. Örneğin, Cantor veya Baire uzayının her alt kümesi bir kümedir (yani, sayılabilir sayıda açık kümenin kesişimine eşit olan bir küme). Ayrıca, bu açık kümelerin her biri birdir ve bu açık kümelerin Gödel numaralarının listesi hesaplanabilir bir numaralandırmaya sahiptir. Eğer a, serbest grubu, değişken ile, formül X ve serbest numara değişkenler daha sonra resim kesişimidir formunun setleri olarak N , doğal sayılar kümesinin üzerinde aralıkları.${\displaystyle \Pi _{2}^{0}}$${\displaystyle G_{\delta }}$${\görüntüleme stili \Sigma _{1}^{0}}$${\görüntüleme stili \phi (X,n,m)}$${\görüntüleme stili \Sigma _{0}^{0}}$${\görüntüleme stili n,m}$${\displaystyle \Pi _{2}^{0}}$${\displaystyle \{X\mid \forall n\vardır m\phi (X,n,m)\}}$${\görüntüleme stili \Sigma _{1}^{0}}$${\displaystyle \{X\mid \var m\phi (X,n,m)\}}$
• Formülleri tüm nicelik sınırlanmış çünkü mümkün olan tek tek her durumda üzerinde giderek kontrol edilebilir. Bunun zamanı argümanlarında polinomdur (örneğin n için polinom ); dolayısıyla bunlara karşılık gelen karar problemleri E'ye dahil edilir ( n , bit sayısında üstel olduğu için). Bu artık, ilkel özyinelemeli işlevlerin kullanımına izin veren alternatif tanımları altında geçerli değildir , çünkü artık niceleyiciler, argümanların herhangi bir ilkel özyinelemeli işlevine bağlı olabilir.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\görüntüleme stili \varphi (n)}$${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$
• Formun tamsayılar kümelerine sınırlı Nicelik, tekabül ilkel yinelemeli fonksiyonların kullanımını sağlayan alternatif bir tanımlama altında formüller ilkel özyinelemeli fonksiyonu f . Bunun nedeni, sınırlı niceleyiciye izin vermenin tanıma hiçbir şey eklememesidir: ilkel bir özyinelemeli f için , ile aynıdır ve ile aynıdır ; ile ders-of-değerleri kendini yineleme bunların her biri tek bir primitif yineleme fonksiyonu ile tanımlanabilir.${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}}$${\displaystyle \{n:f(n)=0\}}$${\displaystyle \forall k<n:f(k)=0}$${\displaystyle f(0)+f(1)+...f(n)=0}$${\görüntüleme stili \vardır k<n:f(k)=0}$${\displaystyle f(0)*f(1)*...f(n)=0}$

Özellikleri

Aşağıdaki özellikler, doğal sayı kümelerinin aritmetik hiyerarşisi ve Cantor veya Baire uzayının alt kümelerinin aritmetik hiyerarşisi için geçerlidir.

• Koleksiyonları ve sonlu altında kapalı sendikalar ve sonlu kavşaklar kendi elemanlarının.${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$
• Bir küme ancak ve ancak tümleyeni ise . Bir küme ancak ve ancak küme hem ve ise, bu durumda tümleyeni de olacaktır .${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}}$${\displaystyle \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}}$
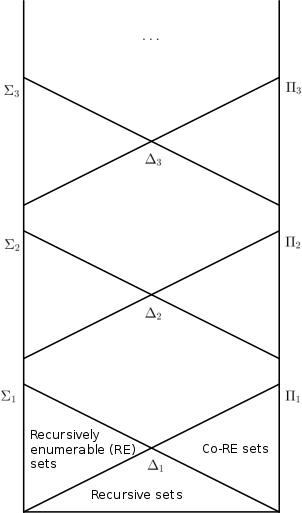
• Kapanımlar ve herkes için bekletme . Böylece hiyerarşi çökmez. Bu, Post teoreminin doğrudan bir sonucudur .${\displaystyle \Pi _{n}^{0}\subsetneq \Pi _{n+1}^{0}}$${\displaystyle \Sigma _{n}^{0}\subsetneq \Sigma _{n+1}^{0}}$${\görüntüleme stili n}$
• Kalıntılar , ve tutma için .${\displaystyle \Delta _{n}^{0}\subsetneq \Pi _{n}^{0}}$${\displaystyle \Delta _{n}^{0}\subsetneq \Sigma _{n}^{0}}$${\displaystyle \Sigma _{n}^{0}\cup \Pi _{n}^{0}\subsetneq \Delta _{n+1}^{0}}$${\displaystyle n\geq 1}$

• Örneğin, evrensel bir Turing makinesi T için, T'nin n üzerinde duracağı ancak m üzerinde durmayacağı (n,m) çiftleri kümesi içindedir (durma problemine ilişkin bir kehanetle hesaplanabilir), ancak , içinde değildir .${\displaystyle \Delta _{2}^{0}}$${\displaystyle \Sigma _{1}^{0}\cup \Pi _{1}^{0}}$
• ${\displaystyle \Sigma _{0}^{0}=\Pi _{0}^{0}=\Delta _{0}^{0}=\Sigma _{0}^{0}\cup \Pi _{0}^{0}\subset \Delta _{1}^{0}}$. Dahil etme, bu makalede verilen tanıma göre katıdır, ancak yukarıda verilen tanımın varyasyonlarından birinin altında bulunan bir özdeşlik vardır .${\displaystyle \Delta _{1}^{0}}$

Turing makineleriyle ilişkisi

hesaplanabilir kümeler

S bir Turing hesaplanabilir kümesi ise , o zaman hem S hem de tümleyeni yinelemeli olarak sayılabilir (eğer T, S'deki girişler için 1 ve 0 veren bir Turing makinesiyse, aksi takdirde, yalnızca birincisi üzerinde duran bir Turing makinesi ve yalnızca birincisi üzerinde duran bir Turing makinesi oluşturabiliriz. ikincisi üzerinde).

By Post'un teoremi , S ve bunun tamamlayıcısı olan . Bu, S'nin hem içinde hem de içinde olduğu ve dolayısıyla içinde olduğu anlamına gelir . ${\görüntüleme stili \Sigma _{1}^{0}}$${\görüntüleme stili \Sigma _{1}^{0}}$${\görüntüleme stili \Pi _{1}^{0}}$${\displaystyle \Delta _{1}^{0}}$

Benzer şekilde, her set için S , S ve bunun tamamlayıcısı olan ve (göre bu nedenle Post teoremi bazı Turing makineleri T) tarafından ardışık enumerable ₁ ve T ₂ , sırasıyla. Her n sayısı için tam olarak bu duraklardan biri. Bu nedenle, bir Turing makinesi T inşa edebileceğini T arasında dönüşümlü ₁ ve T ₂ , durdurulması ve 1 önceki durur veya durdurulması dönen ve ikinci tarafı durur 0 geri gönderilmesi. Böylece T her n'de durur ve S'de olup olmadığını döndürür, O halde S hesaplanabilirdir. ${\displaystyle \Delta _{1}^{0}}$${\görüntüleme stili \Sigma _{1}^{0}}$

Ana sonuçların özeti

Turing hesaplanabilir doğal sayılar kümeleri, tam olarak aritmetik hiyerarşi düzeyindeki kümelerdir . Yinelemeli olarak numaralandırılabilir kümeler tam olarak level kümesidir . ${\displaystyle \Delta _{1}^{0}}$${\görüntüleme stili \Sigma _{1}^{0}}$

Hiçbir oracle makinesi kendi durma problemini çözemez (Turing'in ispatının bir varyasyonu geçerlidir). Bir kahin için durma sorunu aslında . ${\displaystyle \Delta _{n}^{0,Y}}$${\displaystyle \Sigma _{n+1}^{0,Y}}$

Post'un teoremi , doğal sayı kümelerinin aritmetik hiyerarşisi ile Turing dereceleri arasında yakın bir bağlantı kurar . Özellikle, tüm n ≥ 1 için aşağıdaki gerçekleri belirler :

• Grubu ( N inci Turing atlama boş kümesinin) olan çok-on tam olarak .${\displaystyle \emptyset ^{(n)}}$${\displaystyle \Sigma _{n}^{0}}$
• Set içinde çok-bir tamamlandı .${\displaystyle \mathbb {N} \setminus \emptyset ^{(n)}}$${\displaystyle \Pi _{n}^{0}}$
• Set edilir komple Turing in .${\displaystyle \emptyset ^{(n-1)}}$${\displaystyle \Delta _{n}^{0}}$

Polinom hiyerarşi polinom uzunluk sınırları katılan numaralar (veya buna eşdeğer polinom zaman sınırları yer Turing makineleri yerleştirilir) üzerine yerleştirildikleri aritmetik hiyerarşi "uygulanabilir kaynak sınırlanmış" versiyonudur. Aritmetik hiyerarşi düzeyinde olan bazı doğal sayı kümelerinin daha iyi bir sınıflandırmasını verir . ${\displaystyle \Delta _{1}^{0}}$

Diğer hiyerarşilerle ilişkisi

Ayrıca bakınız

• Vergi hiyerarşisi
• Hiyerarşi (matematik)
• yorumlanabilirlik mantığı
• polinom hiyerarşisi

Referanslar