İzomorfizm teoremleri - Isomorphism theorems

Gelen matematik , özellikle soyut cebir , izomorfizm teoremi (aynı zamanda Noether'in izomorfizm teoremi ) olan teoremi arasındaki ilişkiyi açıklar katsayılar , homomorfizmalar ve alt nesne . Gruplar , halkalar , vektör uzayları , modüller , Lie cebirleri ve diğer çeşitli cebirsel yapılar için teoremlerin versiyonları mevcuttur . Gelen evrensel cebir , izomorfizm teoremleri Cebirlerin ve bağlamında jeneralize olabilir kongrüanslar .

Tarih

İzomorfizm teoremleri, Emmy Noether tarafından 1927'de Mathematische Annalen'de yayınlanan Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern adlı makalesinde modüllerin homomorfizmaları için bazı genellikte formüle edildi . Bu teoremlerin daha az genel versiyonları, Richard Dedekind'in çalışmalarında ve Noether'in önceki makalelerinde bulunabilir.

Üç yıl sonra, BL van der Waerden , konuya grup - halka - alan yaklaşımını alan ilk soyut cebir ders kitabı olan etkili Moderne Cebir kitabını yayınladı . Van der Waerden, Noether'in grup teorisi ve Emil Artin'in cebir üzerine verdiği derslerin yanı sıra Artin, Wilhelm Blaschke , Otto Schreier ve van der Waerden'in kendisi tarafından idealler üzerine yürütülen bir semineri ana referanslar olarak kabul etti. Homomorfizm teoremi olarak adlandırılan üç izomorfizm teoremi ve gruplara uygulandığında iki izomorfizm yasası açıkça görünür.

Gruplar

İlk önce grupların izomorfizm teoremlerini sunuyoruz .

Numaralar ve isimlerle ilgili not

Aşağıda A, B, C ve D olarak etiketlenmiş dört teorem sunuyoruz. Bunlar genellikle "Birinci izomorfizm teoremi", "İkinci..." vb. olarak numaralandırılır; ancak, numaralandırma konusunda evrensel bir anlaşma yoktur. Burada literatürdeki grup izomorfizm teoremlerinin bazı örneklerini veriyoruz. Bu teoremlerin halkalar ve modüller için analogları olduğuna dikkat edin.

Grup izomorfizm teoremlerinin adlarının karşılaştırılması

	Yazar	Teorem A	Teorem B	Teorem C
"Üçüncü" teorem yok	Jacobson	Homomorfizmaların temel teoremi	(ikinci izomorfizm teoremi)	" genellikle ilk izomorfizm teoremi olarak adlandırılır "
	van der Waerden, Durbin	Homomorfizmaların temel teoremi	ilk izomorfizm teoremi	ikinci izomorfizm teoremi
	Knapp	(isimsiz)	İkinci izomorfizm teoremi	Birinci izomorfizm teoremi
	ızgara	homomorfizma teoremi	İkinci izomorfizm teoremi	Birinci izomorfizm teoremi
Üç numaralı teorem	(Grillet'te belirtilen diğer sözleşme)	Birinci izomorfizm teoremi	Üçüncü izomorfizm teoremi	İkinci izomorfizm teoremi
	Rotman	Birinci izomorfizm teoremi	İkinci izomorfizm teoremi	Üçüncü izomorfizm teoremi
	Fraleeigh	(isimsiz)	İkinci izomorfizm teoremi	Üçüncü izomorfizm teoremi
	Aptal ve Ayak	Birinci izomorfizm teoremi	İkinci veya Elmas izomorfizm teoremi	Üçüncü izomorfizm teoremi
numaralandırma yok	Milne	homomorfizma teoremi	izomorfizm teoremi	tekabül teoremi
	Scott	homomorfizma teoremi	izomorfizm teoremi	birinci sınıf teoremi

Genellikle " kafes teoremi " veya "karşılık teoremi" olarak bilinen Teorem D'yi izomorfizm teoremlerinden birine dahil etmek daha az yaygındır , ancak yaptıklarında, sonuncusu olur.

Teoremlerin ifadesi

Teorem A (gruplar)

Let G ve H grupları ve izin f :  G  →  H bir olmak homomorfizması . Sonra:

1. Çekirdek ve f a, normal bir alt-grup içinde , G ,
2. Görüntü ve f a, alt grup arasında H ve
3. Görüntü f olan izomorfik için bölüm grubu G  / ker ( f ).

Özellikle, ön olan örten sonra , H izomorf G  / ker ( f ).

Teorem B (gruplar)

Izin bir grup. ' nin bir alt grubu olsun ve ' nin normal bir alt grubu olsun . Ardından aşağıdaki tutun: ${\görüntüleme stili G}$${\görüntüleme stili S}$${\görüntüleme stili G}$${\görüntüleme stili N}$${\görüntüleme stili G}$

1. Ürün bir alt grubudur ,${\görüntüleme stili SN}$${\görüntüleme stili G}$
2. Kesişme normal bir alt grubudur , ve${\ Displaystyle S\cap N}$${\görüntüleme stili S}$
3. Bölüm grupları ve izomorfiktir.${\görüntüleme stili (SN)/N}$${\ Displaystyle S/(S\cap N)}$

İçin Teknik olarak gerekli değildir sürece, normal bir alt-grup için bir alt grubudur normalleştirici bir bölgesi . Bu durumda, kesişim ' nin normal bir alt grubu değildir , ancak yine de 'nin normal bir alt grubudur . ${\görüntüleme stili N}$${\görüntüleme stili S}$${\görüntüleme stili N}$${\görüntüleme stili G}$${\ Displaystyle S\cap N}$${\görüntüleme stili G}$${\görüntüleme stili S}$

Bu teorem bazen "izomorfizm teoremi", "elmas teoremi" veya "paralelkenar teoremi" olarak adlandırılır.

İkinci izomorfizm teoreminin bir uygulaması, projektif lineer grupları tanımlar : örneğin, karmaşık projektif çizgi üzerindeki grup, set ile başlar , ters çevrilebilir 2x2 karmaşık matrisler grubu, determinant 1 matrislerinin alt grubu ve skalerin normal alt grubu matrisler , elimizde , kimlik matrisi nerede ve . Sonra ikinci izomorfizm teoremi şunu belirtir: ${\displaystyle G=GL_{2}(\mathbb {C} )}$${\displaystyle S=SL_{2}(\mathbb {C} )}$${\görüntüleme stili N}$${\displaystyle \mathbb {C} ^{\times }\!I=\left\{{\bigl (}{\begin{smallmatrix}a&0\\0&a\end{smallmatrix}}{\bigr )}:a\ \mathbb {C} ^{\times }\right\}} içinde$${\displaystyle S\cap N=\{\pm I\}}$${\görüntüleme stili I}$${\displaystyle SN=GL_{2}(\mathbb {C} )}$

${\displaystyle PGL_{2}(\mathbb {C} ):=GL_{2}(\mathbb {C} )/(\mathbb {C} ^{\times }\!I)\cong SL_{2}( \mathbb {C} )/\{\pm I\}=:PSL_{2}(\mathbb {C} )}$

Teorem C (gruplar)

Bir grup ve normal bir alt grubu olsun . Sonra ${\görüntüleme stili G}$${\görüntüleme stili N}$${\görüntüleme stili G}$

1. Eğer bir alt grubudur , öyle ki , daha sonra bir alt grup izomorfik sahiptir .${\görüntüleme stili K}$${\görüntüleme stili G}$${\displaystyle N\alt küme K\alt küme G}$${\görüntüleme stili G/N}$${\görüntüleme stili K/N}$
2. Her alt grubu , öyle ki bazı alt grupları için formdadır .${\görüntüleme stili G/N}$${\görüntüleme stili K/N}$${\görüntüleme stili K}$${\görüntüleme stili G}$${\displaystyle N\alt küme K\alt küme G}$
3. Eğer normal bir alt grubudur , öyle ki , daha sonra izomorf normal bir alt grubunu alır .${\görüntüleme stili K}$${\görüntüleme stili G}$${\displaystyle N\alt küme K\alt küme G}$${\görüntüleme stili G/N}$${\görüntüleme stili K/N}$
4. Her normal alt formun olan bazı normal bir alt grup için, bir şekilde .${\görüntüleme stili G/N}$${\görüntüleme stili K/N}$${\görüntüleme stili K}$${\görüntüleme stili G}$${\displaystyle N\alt küme K\alt küme G}$
5. Eğer normal bir alt grubudur , öyle ki daha sonra bölüm grubu, izomorf .${\görüntüleme stili K}$${\görüntüleme stili G}$${\displaystyle N\alt küme K\alt küme G}$${\görüntüleme stili (G/N)/(K/N)}$${\görüntüleme stili G/K}$

Teorem D (gruplar)

Yazışmalar teoremi (aynı zamanda kafes teoremi olarak da bilinir), bazen üçüncü veya dördüncü izomorfizm teoremi olarak adlandırılır.

Zassenhaus lemması (ayrıca kelebek lemma olarak da bilinir), bazen dördüncü izomorfizm teoremi olarak adlandırılır.

Tartışma

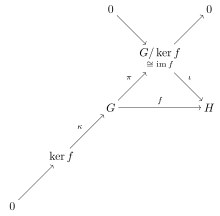
Birinci izomorfizm teoremi, gruplar kategorisinin (normal epi, mono)-faktörize edilebilir olduğunu söyleyerek kategori teorik dilinde ifade edilebilir; başka bir deyişle, normal epimorfizmler ve monomorfizmler , kategori için bir çarpanlara ayırma sistemi oluşturur. Bu, varlığı morfizmden çıkarsanabilecek nesneleri ve morfizmleri gösteren kenar boşluğundaki değişmeli diyagramda yakalanır . Diyagram, gruplar kategorisindeki her morfizmin teorik anlamda kategoride bir çekirdeğe sahip olduğunu göstermektedir ; keyfi morfizm f faktörleri , burada ι bir monomorfizmdir ve π bir epimorfizmdir (bir konormal kategoride, tüm epimorfizmler normaldir). Bu, diyagramda bir nesne ve bir monomorfizm (çekirdekler her zaman monomorfizmdir) ile temsil edilir, bunlar diyagramın sol alt köşesinden sağ üst köşesine uzanan kısa tam diziyi tamamlar . Tam sırası kongre kullanımı çizmek zorunda bizi kurtarır sıfır morfizimler gelen etmek ve . ${\ Displaystyle f:G\rightarrow H}$${\ Displaystyle \ iota \ circ \ pi }$${\görüntüleme stili \ker f}$${\displaystyle \kappa :\ker f\rightarrow G}$${\görüntüleme stili \ker f}$${\görüntüleme stili H}$${\displaystyle G/\ker f}$

Sekansı, sağ bölüm (yani, bir morfizmanın vardır ise σ haritalar a π kendisi -preimage), daha sonra G ise semidirect ürün , normal bir alt-grubu ve bir alt-grubu . Sol bölünmüş ise (yani, bazı mevcut şekilde , o zaman da sağ bölünmüş olmalıdır) ve bir olan doğrudan ürün ayrışması G . Genel olarak, bir sağ bölünmenin varlığı, bir sol bölünmenin varlığını ima etmez; ancak değişmeli bir kategoride (örneğin değişmeli gruplar), sol bölmeler ve sağ bölmeler bölme lemması ile eşdeğerdir ve doğrudan toplam ayrıştırma üretmek için bir sağ bölme yeterlidir . Değişken bir kategoride, tüm monomorfizmler de normaldir ve diyagram ikinci bir kısa tam dizi ile genişletilebilir . ${\displaystyle G/\ker f}$${\displaystyle \operatöradı {im} \kappa }$${\displaystyle \operatöradı {im} \sigma }$${\displaystyle \rho :G\rightarrow\ker f}$${\displaystyle \rho \circ \kappa =\operatöradı {id} _{\ker f}}$${\displaystyle \operatöradı {im} \kappa \times \operatöradı {im} \sigma }$${\displaystyle \operatöradı {im} \kappa \oplus \operatöradı {im} \sigma }$${\displaystyle 0\rightarrow G/\ker f\rightarrow H\rightarrow \operatör adı {coker} f\rightarrow 0}$

İkinci izomorfizm teoremi, ürün SN olan birleştirme bölgesinin S ve N bölgesindeki alt kafes arasında G kesişme ise, S  ∩  N olduğu bir araya .

Üçüncü izomorfizm teoremi, dokuz lemma tarafından değişmeli kategorilere ve nesneler arasındaki daha genel haritalara genelleştirilir .

Yüzükler

Halkalar için teoremlerin ifadeleri , bir ideal kavramı ile değiştirilen normal bir alt grup kavramı ile benzerdir .

Teorem A (halkalar)

Let R ve S halkaları olabilir ve izin φ :  R  →  S bir olmak halka homomorfizması . Sonra:

1. Çekirdek ve cp arasında bir idealdir R ,
2. Görüntü ve cp a, alt halka ve S , ve
3. φ'nin görüntüsü , bölüm halkası R  / ker( φ ) ile eşbiçimlidir .

Özellikle, φ olan örten sonra S izomorf R  / ker ( φ ).

Teorem B (halkalar)

Let R, bir halka meydana. Let S bir alt halka olmak R ve izin ben bir ideal R . Sonra:

1. Toplam S  +  I  = { s  +  i  | s  ∈  S ,  i  ∈  I } R'nin bir alt halkasıdır ,
2. Kesişme S  ∩  ı bir tanesi olan S ve
3. Bölüm halkaları ( S  +  I ) /  I ve S  / ( S  ∩  I ) izomorfiktir.

Teorem C (halkalar)

Let R, bir halka olabilir ve bir ideal R . Sonra

1. Eğer bir alt halka olduğunu , öyle ki , daha sonra bir alt halka olduğunu .${\görüntüleme stili A}$${\görüntüleme stili R}$${\displaystyle I\subseteq A\subseteq R}$${\görüntüleme stili A/I}$${\görüntüleme stili R/I}$
2. Her alt halka formunun olan bazı bölüm halkasının için, bir şekilde .${\görüntüleme stili R/I}$${\görüntüleme stili A/I}$${\görüntüleme stili A}$${\görüntüleme stili R}$${\displaystyle I\subseteq A\subseteq R}$
3. Eğer bir ideal şekilde , daha sonra bir idealdir .${\görüntüleme stili J}$${\görüntüleme stili R}$${\displaystyle I\subseteq J\subseteq R}$${\görüntüleme stili J/I}$${\görüntüleme stili R/I}$
4. Her İdeal formu olan bazı ideali için, bir şekilde .${\görüntüleme stili R/I}$${\görüntüleme stili J/I}$${\görüntüleme stili J}$${\görüntüleme stili R}$${\displaystyle I\subseteq J\subseteq R}$
5. Eğer bir ideal şekilde daha sonra bölüm halkası, izomorfiktir .${\görüntüleme stili J}$${\görüntüleme stili R}$${\displaystyle I\subseteq J\subseteq R}$${\görüntüleme stili (R/I)/(J/I)}$${\görüntüleme stili R/J}$

Teorem D (halkalar)

ideali olsun . Yazışma alt halkalar grubu arasında bir inklüzyon koruyucu bijection olan arasında ihtiva ve alt halkalar grubu . Ayrıca, (içeren bir alt halka ), ancak ve ancak bir ideal ise bir idealdir . ${\görüntüleme stili I}$${\görüntüleme stili R}$${\displaystyle A\leftrightarrow A/I}$${\görüntüleme stili A}$${\görüntüleme stili R}$${\görüntüleme stili I}$${\görüntüleme stili R/I}$${\görüntüleme stili A}$${\görüntüleme stili I}$${\görüntüleme stili R}$${\görüntüleme stili A/I}$${\görüntüleme stili R/I}$

Modüller

Modüller için izomorfizm teoremlerinin ifadeleri, herhangi bir alt modülden bir bölüm modülü oluşturmak mümkün olduğundan özellikle basittir . Vektör uzayları (alan üzerindeki modüller) ve değişmeli gruplar (modüller üzeri ) için izomorfizm teoremleri bunların özel durumlarıdır. Sonlu boyutlu vektör uzayları için, bu teoremlerin tümü sıra-boşluk teoreminden çıkar . ${\displaystyle \mathbb {Z} }$

Aşağıda "modül", bazı sabit R halkası için " R- modülü" anlamına gelecektir .

Teorem A (modüller)

Let M ve N modülleri olabilir ve izin φ :  M  →  N bir olmak modül homomorfizması . Sonra:

1. Çekirdek bir cp bir alt modül olup M ,
2. Görüntü bir cp bir alt modül olup , N ve
3. φ'nin görüntüsü M  / ker( φ ) bölüm modülüne eşbiçimlidir .

Özellikle, eğer φ surjective ise , o zaman N , M  / ker( φ ) ile izomorfiktir .

Teorem B (modüller)

Let M bir modül olabilir ve izin S ve T arasında alt modül olabilir M . Sonra:

1. Toplam S  +  T  = { s  +  t  | s  ∈  S ,  t  ∈  T } M'nin bir alt modülüdür ,
2. S  ∩  T kesişimi M'nin bir alt modülüdür ve
3. Bölüm modülleri ( S  +  T ) /  T ve S  / ( S  ∩  T ) izomorfiktir.

Teorem C (modüller)

M bir modül, T ise M'nin bir alt modülü olsun .

1. Eğer bir alt modül olduğunu , öyle ki , daha sonra bir alt modül olduğunu .${\görüntüleme stili S}$${\görüntüleme stili M}$${\displaystyle T\alt küme S\alt küme M}$${\ Displaystyle S/T}$${\ Displaystyle M/T}$
2. Her alt modül formunun olan bazı altmodülün için, bir şekilde .${\ Displaystyle M/T}$${\ Displaystyle S/T}$${\görüntüleme stili S}$${\görüntüleme stili M}$${\displaystyle T\alt küme S\alt küme M}$
3. Eğer bir alt modül olduğunu , öyle ki daha sonra katsayısı modül, izomorfiktir .${\görüntüleme stili S}$${\görüntüleme stili M}$${\displaystyle T\alt küme S\alt küme M}$${\görüntüleme stili (M/T)/(S/T)}$${\ Displaystyle M/S}$

Teorem D (modüller)

Bir modül, bir alt modül olsun . İçindeki modüllerin arasında bir bijection vardır o içerirler ve içindeki modüllerin . Yazışma herkes için tarafından verilir . Toplamları ve kavşakları alma işlemleri ile bu yazışma yolculukları (yani, alt birimlerin kafes arasında bir kafes izomorfizm olan ve alt birimlerin kafes bu içerir ). ${\görüntüleme stili M}$${\görüntüleme stili N}$${\görüntüleme stili M}$${\görüntüleme stili M}$${\görüntüleme stili N}$${\görüntüleme stili M/N}$${\displaystyle A\leftrightarrow A/N}$${\ Displaystyle A\supseteq N}$${\görüntüleme stili M/N}$${\görüntüleme stili M}$${\görüntüleme stili N}$

evrensel cebir

Bunu evrensel cebire genellemek için , normal alt grupların uyum ilişkileriyle değiştirilmesi gerekir .

Bir cebir üzerinde kongrüans , bir cebir olarak kabul edilen bir cebir alt cebiri oluşturan bir denklik bağıntısıdır . İşlemler temsilciler aracılığıyla tanımlanarak, denklik sınıfları kümesi aynı türden bir cebir haline getirilebilir; ' nin bir alt cebiri olduğundan bu iyi tanımlanmış olacaktır . Ortaya çıkan yapı bölüm cebiridir . ${\görüntüleme stili A}$${\displaystyle \Phi \subseteq A\times A}$${\ Displaystyle A\time A}$${\görüntüleme stili A/\Phi }$${\görüntüleme stili\Phi }$${\ Displaystyle A\time A}$

Teorem A (evrensel cebir)

Izin bir cebir olmak homomorfizması . Sonra görüntü bir alt cebiri olan , verilen bir ilişki (yani çekirdek içinde ) ile bir uyum olduğunu ve cebir ve izomorfik. (Bir grup söz konusu olduğunda, iff , bu durumda, bu durumda grup teorisinde kullanılan çekirdek kavramını kurtardığını unutmayın.) ${\ Displaystyle f:A\sağ ok B}$${\görüntüleme stili f}$${\görüntüleme stili B}$${\görüntüleme stili \Phi :f(x)=f(y)}$${\görüntüleme stili f}$${\görüntüleme stili A}$${\ Displaystyle \ A/\ Phi \ }$${\displaystyle \operatöradı {im} f}$${\görüntüleme stili f(x)=f(y)}$${\displaystyle f\sol(xy^{-1}\sağ)=1}$

Teorem B (evrensel cebir)

Bir cebir Verilen bir alt cebiri ait ve bir eşleşmeyi üzerine , let eser olması halinde ve denklik sınıflarının koleksiyonu olduğu kesiştiği . Sonra ${\görüntüleme stili A}$${\görüntüleme stili B}$${\görüntüleme stili A}$${\görüntüleme stili\Phi }$${\görüntüleme stili A}$${\displaystyle \Phi _{B}=\Phi \cap (B\time B)}$${\görüntüleme stili\Phi }$${\görüntüleme stili B}$${\displaystyle [B]^{\Phi }=\{K\in A/\Phi :K\cap B\neq \emptyset \}}$${\görüntüleme stili B}$

1. ${\görüntüleme stili \Phi _{B}}$üzerinde bir uyumdur ,${\görüntüleme stili B}$
2. ${\ Displaystyle \ [B]^{\Phi }}$'nin bir alt cebiridir ve${\görüntüleme stili A/\Phi }$
3. cebir cebire eşbiçimlidir .${\görüntüleme stili [B]^{\Phi }}$${\ Displaystyle B/\Phi _{B}}$

Teorem C (evrensel cebir)

Izin bir cebir ve olmayacak iki uyum ilişkileri öyle ki . O zaman üzerinde bir kongrüans ve ile izomorfiktir . ${\görüntüleme stili A}$${\görüntüleme stili\Phi ,\Psi }$${\görüntüleme stili A}$${\displaystyle \Psi \subseteq \Phi }$${\displaystyle \Phi /\Psi =\{([a']_{\Psi },[a'']_{\Psi }):(a',a'')\in \Phi \}=[ \ ]_{\Psi }\circ \Phi \circ [\ ]_{\Psi }^{-1}}$${\görüntüleme stili A/\Psi }$${\görüntüleme stili A/\Phi }$${\görüntüleme stili (A/\Psi )/(\Phi /\Psi )}$

Teorem D (evrensel cebir)

Izin bir cebir olmak ve göstermek tüm kongrüansların kümesi . Set , dahil edilerek sıralanmış tam bir kafestir. Eğer bir uyum ve biz tarafından ifade içeren tüm kongrüansların kümesi (yani bir müdürüdür filtre içinde , daha sonra harita dahası bir alt a˘gdaki olduğunu) bir kafes izomorfizması olduğunu. ${\görüntüleme stili A}$${\displaystyle \operatöradı {Con} A}$${\görüntüleme stili A}$${\displaystyle \operatöradı {Con} A}$${\displaystyle \Phi \in \operatöradı {Con} A}$${\displaystyle \sol[\Phi ,A\times A\right]\subseteq \operatöradı {Con} A}$${\görüntüleme stili\Phi }$${\displaystyle \sol[\Phi ,A\times A\sağ]}$${\displaystyle \operatöradı {Con} A}$${\displaystyle \alpha :\left[\Phi ,A\times A\right]\to \operatorname {Con} (A/\Phi ),\Psi \mapsto \Psi /\Phi }$

Not

Referanslar

• Emmy Noether , Abstrakter Aufbau der Idealtheorie cebirsel olarak Zahl- und Funktionenkörpern , Mathematische Annalen 96 (1927) s. 26–61
• Colin McLarty , "Emmy Noether'in 'Set Teorik' Topolojisi: Dedekind'den functorların yükselişine". Modern Matematiğin Mimarisi: Tarih ve felsefede denemeler ( Jeremy Gray ve José Ferreirós tarafından düzenlendi ), Oxford University Press (2006) s. 211–35.
• Jacobson, Nathan (2009), Temel cebir , 1 (2. baskı), Dover, ISBN 9780486471891
• Paul M. Cohn, Evrensel cebir , Bölüm II.3 s. 57
• Milne, James S. (2013), Grup Teorisi , 3.13
• van der Waerden, BI (1994), Cebir , 1 (9 baskı), Springer-Verlag
• Dummit, David S.; Foote, Richard M. (2004). Soyut cebir . Hoboken, NJ: Wiley. ISBN'si 978-0-471-43334-7.
• Burris, Stanley; Sankappanavar, HP (2012). Evrensel Cebir Kursu (PDF) . ISBN'si 978-0-9880552-0-9.
• WR Scott (1964), Grup Teorisi , Prentice Hall
• John R. Durbin (2009). Modern Cebir: Bir Giriş (6 ed.). Wiley. ISBN'si 978-0-470-38443-5.
• Anthony W. Knapp (2016), Temel Cebir (Dijital ikinci baskı)
• Pierre Antoine Grillet (2007), Soyut Cebir (2 ed.), Springer
• Joseph J. Rotman (2003), İleri Modern Cebir (2 ed.), Prentice Hall, ISBN 0130878685