Alt grupların kafesi - Lattice of subgroups

İki yüzlü grup Dih 4'ün alt gruplarının kafeslerinin, döngü grafikleri ile temsil edilen alt grupların Hasse diyagramı

Gelen matematik , alt kafes a grubu olan kafes öğesi olan alt gruplar arasında olan, kısmi sıralama ilişkisi olmak grubu dahil . Bu kafeste, iki alt grubun birleşimi , birleşmeleri tarafından oluşturulan alt gruptur ve iki alt grubun buluşması, bunların kesişimidir .

Misal

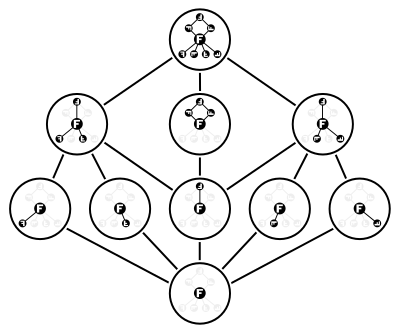
Dihedral grubu Dih 4 kendisi ve sayma, on alt gruba önemsiz alt grup . Sekiz grup elemanından beşi ikinci dereceden alt gruplar oluşturur ve diğer iki özdeş olmayan elemanın her ikisi de dördüncü dereceden aynı döngüsel alt grubu üretir . Ek olarak, iki sıra eleman çiftleri tarafından üretilen Z 2 × Z 2 şeklinde iki alt grup vardır . Bu on alt grup tarafından oluşturulan kafes, şekilde gösterilmiştir.

Bu örnek ayrıca bir grubun tüm alt gruplarının kafesinin genel olarak modüler bir kafes olmadığını gösterir . Aslında, bu belirli kafes, bir alt örgü olarak yasaklanmış "beşgen" N 5'i içerir .

Özellikleri

Herhangi biri için bir , B , ve C ile bir grup alt bir ≤ C ( bir alt-grubu C ), daha sonra AB ∩ C = A (B ∩ C) ; buradaki çarpma , alt grupların çarpımıdır . Bu özellik, grupların modüler özelliği ( Aschbacher 2000 ) veya ( Dedekind'in ) modüler yasası ( Robinson 1996 , Cohn 2000 ) olarak adlandırılmıştır. İki normal alt grup için ürün aslında ikisini içeren en küçük alt grup olduğundan, normal alt gruplar modüler bir kafes oluşturur .

Kafes teoremi oluşturan bir Galois'in bağlantı grubunun alt kafes ve katsayılarının arasındaki.

Zassenhaus lemması alt kafes yapısındaki katsayılarının ve ürünlerin belirli kombinasyonlar arasında bir izomorfizm verir.

Genel olarak, her kafesin bir grubun alt grup kafesinin bir alt kafesine izomorfik olması anlamında, alt grupların kafesinin şekli üzerinde herhangi bir kısıtlama yoktur. Ayrıca, her sonlu kafes, bazı sonlu grupların alt grup kafesinin bir alt örgüsüne izomorfiktir ( Schmidt 1994 , s. 9).

Karakteristik kafesler

Belirli özelliklere sahip alt gruplar kafesler oluşturur, ancak diğer özellikler oluşturmaz.

  • Normal alt gruplar her zaman modüler bir kafes oluşturur. Aslında, kafesin modüler olmasını garanti eden temel özellik, alt grupların birbiriyle gidip gelmesidir , yani bunların yarı normal alt gruplar olmalarıdır .
  • Nilpotent normal alt grupları, Fitting teoreminin içeriğinin (bir parçası olan) bir kafes oluşturur .
  • Genel olarak, herhangi bir Fitting sınıfı F için , hem normal altı F alt grupları hem de normal F alt grupları kafesleri oluşturur. Bu, yukarıdaki F ile üstelsıfır gruplar sınıfını ve aynı zamanda F çözülebilir gruplar sınıfı gibi diğer örnekleri içerir . Bir grup sınıfı, izomorfizm, normal altı alt gruplar ve normal altı alt grupların ürünleri altında kapalıysa Fitting sınıfı olarak adlandırılır.
  • Merkezi alt gruplar bir kafes oluşturur.

Bununla birlikte, ne sonlu alt gruplar ne de burulma alt grupları bir kafes oluşturmaz: örneğin, serbest ürün iki burulma elemanı tarafından üretilir, ancak sonsuzdur ve sonsuz mertebeden elemanlar içerir.

Normal alt grupların modüler bir kafes oluşturması gerçeği, daha genel bir sonucun özel bir örneğidir, yani herhangi bir Maltsev çeşidinde (bu grupların bir örneğidir), kongrüans kafesi modülerdir ( Kearnes & Kiss 2013 ).

Grupları alt grup kafeslerine göre karakterize etme

Alt grupların kafesi hakkındaki kafes teorik bilgileri bazen orijinal grup hakkında bilgi çıkarmak için kullanılabilir, bu fikir Øystein Ore'un  ( 1937 , 1938 ) çalışmasına geri döner . Cevher kanıtladı Örneğin, bir grup olduğu , yerel olarak, siklik ve eğer alt kendi kafes yalnızca dağıtım . Ek olarak kafes yükselen zincir koşulunu karşılarsa , grup döngüseldir.

Alt grup örgüsü tamamlanmış bir kafes olan gruplara tamamlanmış gruplar ( Zacher 1953 ) ve alt gruplarının örgüsü modüler kafesler olan gruplara Iwasawa grupları veya modüler gruplar denir ( Iwasawa 1941 ). Çözülebilir gruplar ve mükemmel gruplar için bu türden kafes-teorik karakterizasyonlar da mevcuttur ( Suzuki 1951 ).

Referanslar

  • Aschbacher, M. (2000). Sonlu Grup Teorisi . Cambridge University Press. s. 6. ISBN   978-0-521-78675-1 .
  • Baer Reinhold (1939). "Grubun yapısı için alt gruplar sisteminin önemi". Amerikan Matematik Dergisi . Johns Hopkins Üniversitesi Yayınları. 61 (1): 1–44. doi : 10.2307 / 2371383 . JSTOR   2371383 .
  • Cohn, Paul Moritz (2000). Klasik cebir . Wiley. s. 248. ISBN   978-0-471-87731-8 .
  • Iwasawa, Kenkiti (1941), "Über die endlichen Gruppen und die Verbände ihrer Untergruppen", J. Fac. Sci. Göstr. Üniv. Tokyo. Mezhep. I. , 4 : 171–199, MR   0005721
  • Kearnes, Keith; Öpücük Emil W. (2013). Eşlik Kafeslerinin Şekli . American Mathematical Soc. s. 3. ISBN   978-0-8218-8323-5 .
  • Cevher, Øystein (1937). "Yapılar ve grup teorisi. I". Duke Matematiksel Dergisi . 3 (2): 149-174. doi : 10.1215 / S0012-7094-37-00311-9 . MR   1545977 .
  • Cevher, Øystein (1938). "Yapılar ve grup teorisi. II". Duke Matematiksel Dergisi . 4 (2): 247–269. doi : 10.1215 / S0012-7094-38-00419-3 . hdl : 10338.dmlcz / 100155 . MR   1546048 .
  • Robinson, Derek (1996). Gruplar Teorisi Kursu . Springer Science & Business Media. s. 15. ISBN   978-0-387-94461-6 .
  • Rottlaender, Ada (1928). "Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Durum der Untergruppen". Mathematische Zeitschrift . 28 (1): 641–653. doi : 10.1007 / BF01181188 . S2CID   120596994 .
  • Schmidt, Roland (1994). Grupların Alt Grup Kafesleri . Matematikte Sergiler. 14 . Walter de Gruyter. ISBN   978-3-11-011213-9 . Bull, Ralph Freese tarafından gözden geçirildi. AMS 33 (4): 487-492.
  • Suzuki, Michio (1951). "Sonlu grupların alt gruplarının kafesi üzerine" . Amerikan Matematik Derneği İşlemleri . Amerikan Matematik Derneği. 70 (2): 345–371. doi : 10.2307 / 1990375 . JSTOR   1990375 . CS1 Maint: önerilmeyen parametre ( bağlantı )
  • Suzuki, Michio (1956). Bir Grubun Yapısı ve Alt Grup Kafesinin Yapısı . Berlin: Springer Verlag. CS1 Maint: önerilmeyen parametre ( bağlantı )
  • Yakovlev, BV (1974). "Bir kafesin, bir grubun alt gruplarının bir kafesine izomorfik olduğu koşullar". Cebir ve Mantık . 13 (6): 400–412. doi : 10.1007 / BF01462952 . S2CID   119943975 .
  • Zacher Giovanni (1953). "Caratterizzazione dei gruppi risolubili d'ordine finito tamamlayıcı" . Rendiconti del Seminario Matematico della Università di Padova . 22 : 113–122. ISSN   0041-8994 . MR   0057878 .

Dış bağlantılar