cebirsel eğri - Algebraic curve

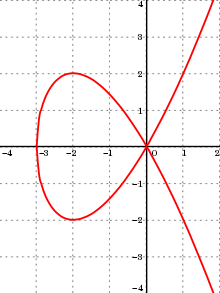
Gelen matematik bir afin cebirsel düzlem eğri olan sıfır grubu a polinom iki değişken. Bir yansıtmalı cebirsel düzlem eğri bir sıfır dizi yansıtmalı düzleme a homojen bir polinom üç değişken olarak. Bir projektif cebirsel düzlem eğrisinde , tanımlayıcı polinomunu homojenleştirerek bir afin cebirsel düzlem eğrisi tamamlanabilir . Bunun tersine, h ( x , y , t ) = 0 homojen denkleminin projektif cebirsel düzlem eğrisi, h ( x , y , 1) = 0 denkleminin afin cebirsel düzlem eğrisi ile sınırlandırılabilir . Bu iki işlemin her biri diğerinin tersidir ; bu nedenle, cebirsel düzlem eğrisi ifadesi genellikle, dikkate alınanın afin mi yoksa projektif durum mu olduğu açıkça belirtilmeden kullanılır.

Daha genel olarak, bir cebirsel eğri bir bir cebirsel çeşitli arasında boyut on. Eşdeğer olarak, bir cebirsel eğri, bir cebirsel düzlem eğrisine çift ​​yönlü olarak eşdeğer olan bir cebirsel çeşittir . Eğri bir afin uzayda veya bir yansıtmalı uzayda yer alıyorsa , böyle bir çift yönlü eşdeğerlik için bir izdüşüm alınabilir.

Bu çift uluslu denklikler, cebirsel eğrilerin incelenmesinin çoğunu cebirsel düzlem eğrilerinin çalışmasına indirger. Bununla birlikte, bazı özellikler birasyonel eşdeğerlik altında tutulmaz ve düzlemsel olmayan eğriler üzerinde çalışılmalıdır. Bu, özellikle, derece ve pürüzsüzlük için geçerlidir . Örneğin, cins 0 ve ikiden büyük dereceli düzgün eğriler vardır , ancak bu tür eğrilerin herhangi bir düzlem izdüşümünün tekil noktaları vardır (bkz. Tür-derece formülü ).

Düzlem olmayan bir eğriye genellikle bir uzay eğrisi veya bir çarpık eğri denir .

Öklid geometrisinde

Öklid düzlemindeki bir cebirsel eğri , koordinatları iki değişkenli bir polinom denklemi p ( x , y ) = 0 olan noktaların kümesidir. Bu denkleme genellikle eğrinin örtük denklemi denir. tanımlayan bir fonksiyon grafiği olan açık bir y bir fonksiyonu olarak , x .

Böyle bir örtük denklem tarafından verilen bir eğri ile, ilk problemler eğrinin şeklini belirlemek ve çizmektir. Bu problemlerin çözülmesi, çeşitli x değerleri için y'nin kolayca hesaplanabileceği bir fonksiyonun grafiğindeki gibi kolay değildir . Tanımlayıcı denklemin bir polinom olması, eğrinin bu problemlerin çözümüne yardımcı olabilecek bazı yapısal özelliklere sahip olduğunu ima eder.

Her cebirsel eğri, bazen "dikkate değer noktalar" olarak adlandırılan bazı noktalarla ve muhtemelen aknodlar olarak adlandırılan sonlu sayıda yalıtılmış noktalarla bağlanan sonlu sayıda düz monoton yaya ( dallar olarak da adlandırılır ) benzersiz bir şekilde ayrıştırılabilir . Bir düz monoton yay bir grafiğidir düzgün fonksiyon tanımlanmıştır ve monoton bir de açık aralığı içinde X -Axis. Her yönde, bir yay ya sınırsızdır (genellikle sonsuz yay olarak adlandırılır ) ya da tekil bir nokta olan (bu aşağıda tanımlanacaktır) ya da koordinat eksenlerinden birine teğet paralel bir nokta olan bir bitiş noktasına sahiptir.

Örneğin, Tschirnhausen kübik için , bitiş noktası itibariyle orijini (0,0) olan iki sonsuz yay vardır. Bu nokta eğrinin tek tekil noktasıdır . Bu tekil noktayı bir bitiş noktası olarak ve yatay bir teğet ile ikinci bir bitiş noktasını içeren iki yay da vardır. Son olarak, her biri birinci uç nokta olarak yatay teğetli bu noktalardan birine ve ikinci uç nokta olarak dikey teğetli benzersiz noktaya sahip olan iki yay daha vardır. Buna karşılık, sinüzoid kesinlikle sonsuz sayıda monoton yaya sahip cebirsel bir eğri değildir.

Cebirsel bir eğri çizmek için, dikkat çekici noktaları ve bunların teğetlerini, sonsuz dalları ve (varsa) asimptotlarını ve yayların bunları nasıl birbirine bağladığını bilmek önemlidir . Bükülme noktalarını da dikkat çekici noktalar olarak değerlendirmekte fayda var . Tüm bu bilgiler bir kağıda çizildiğinde, eğrinin şekli genellikle oldukça net görünür. Değilse, eğrinin iyi bir tanımını elde etmek için birkaç nokta ve bunların teğetlerini eklemek yeterlidir.

Dikkat çekici noktaları ve bunların teğetlerini hesaplama yöntemleri, aşağıda Bir düzlem eğrisinin dikkat çekici noktaları bölümünde açıklanmıştır .

Düzlem projektif eğriler

Projektif uzayda eğrileri dikkate almak genellikle arzu edilir . Projektif düzlemdeki cebirsel eğri veya düzlem projektif eğri , projeksiyonlu koordinatları üç değişken P ( x , y , z ) içinde homojen bir polinomun sıfırları olan bir projektif düzlemdeki noktaların kümesidir .

p ( x , y ) = 0 denkleminin her afin cebirsel eğrisi, denklemin projektif eğrisine tamamlanabilir, burada ${\displaystyle ^{h}p(x,y,z)=0,}$

${\displaystyle ^{h}p(x,y,z)=z^{\deg(p)}p({\tfrac {x}{z}},{\tfrac {y}{z}})}$

sonucudur homojenleştirme ve p . Tersine, eğer P ( x , y , z ) = 0 bir yansıtmalı eğrinin homojen denklemiyse, o zaman P ( x , y , 1) = 0, yansıtmalı eğrinin noktalarından oluşan bir afin eğrinin denklemidir. üçüncü projektif koordinatı sıfır olmayan. Bu iki işlem gibi diğer karşılıklı biri ise ve s ile tanımlanır , daha sonra homojen bir polinom kısa zamanda P tarafından bölünebilir değildir z . ${\görüntüleme stili ^{h}p(x,y,1)=p(x,y)}$${\görüntüleme stili p(x,y)=P(x,y,1)}$${\displaystyle ^{h}p(x,y,z)=P(x,y,z),}$

Örneğin, x ² + y ² − z ² denkleminin yansıtmalı eğrisi, x ² + y ² − 1 = 0 denkleminin birim çemberinin yansıtmalı tamamlanmasıdır .

Bu, afin bir eğrinin ve onun yansıtmalı tamamlanmasının aynı eğriler olduğunu veya daha kesin olarak afin eğrinin, "tam" eğriyi iyi tanımlayacak kadar büyük olan yansıtmalı eğrinin bir parçası olduğu anlamına gelir. Bu bakış açısı, genel olarak afin eğrinin "sonsuzdaki noktaları", afin kısma ait olmayan yansıtmalı tamamlamanın noktaları (sonlu sayıda) olarak adlandırılarak ifade edilir.

Projektif eğriler sıklıkla kendileri için incelenir. Ayrıca afin eğrilerin incelenmesi için de faydalıdırlar. Örneğin, p ( x , y ) kısmi türevlerin yanında bir afin eğri tanımlayan polinom ise ve , sonsuzdaki türevi dikkate almakta fayda var.${\displaystyle p'_{x}}$${\ Displaystyle p'_{y}}$

${\displaystyle p'_{\infty }(x,y)={^{h}p'_{z}(x,y,1)}.}$

Örneğin, p ( x , y ) = 0 denkleminin afin eğrisinin bir ( a , b ) noktasındaki tanjantının denklemi

${\displaystyle xp'_{x}(a,b)+yp'_{y}(a,b)+p'_{\infty }(a,b)=0.}$

Bir düzlem eğrisinin dikkat çekici noktaları

Bu bölümde, iki değişkenli bir polinom p ( x , y ) tarafından tanımlanan bir düzlem cebirsel eğrisini ve p'nin homojenleştirilmesiyle tanımlanan yansıtmalı tamamlanmasını ele alıyoruz . ${\görüntüleme stili P(x,y,z)={}^{h}p(x,y,z)}$

Bir çizgi ile kesişme

Belirli bir doğru ile bir eğrinin kesişme noktalarını bilmek sıklıkla yararlıdır. Koordinat eksenleri ve asimptotlarla kesişme eğriyi çizmek için yararlıdır. Eksenlere paralel bir çizgiyle kesişmek, eğrinin her dalında en az bir noktanın bulunmasını sağlar. Etkili bir kök bulma algoritması varsa, bu, y eksenine paralel tüm doğrularla kesişme noktası çizerek ve x eksenindeki her pikselden geçerek eğrinin çizilmesini sağlar .

Eğriyi tanımlayan polinom d derecesine sahipse , herhangi bir doğru eğriyi en fazla d noktasında keser . Bézout'un teoremi , noktalar cebirsel olarak kapalı bir alan üzerinde (örneğin karmaşık sayılar ) projektif düzlemde aranırsa ve çokluklarıyla sayılırsa , bu sayının tam olarak d olduğunu iddia eder . Aşağıdaki hesaplama yöntemi, bu basit durumda bu teoremi tekrar kanıtlamaktadır.

p polinomu tarafından tanımlanan eğrinin ax + by + c = 0 denkleminin doğrusu ile kesişimini hesaplamak için , doğru denklemi x için (veya a = 0 ise y için) çözülür . Sonucu ikame p , tek tek değişkenli denklem alır q ( y (veya) = 0 q ( X hattının denklemi çözülmüştür ise,) = 0 , y ) kökleri her biri bir kesişme noktasının koordinat, . Diğer koordinat, doğrunun denkleminden çıkarılır. Bir kesişme noktasının çokluğu, karşılık gelen kökün çokluğudur. q'nun derecesi p'nin derecesinden düşükse , sonsuzda bir kesişme noktası vardır ; sonsuzda böyle bir kesişme noktasının çokluğu, p ve q derecelerinin farkıdır .

bir noktada teğet

Eğrinin ( a , b ) noktasındaki teğet, örtük bir denklem tarafından tanımlanan her türevlenebilir eğri için olduğu gibi denklemin doğrusudur. Polinomlar söz konusu olduğunda, tanjant için başka bir formül daha basit bir sabit terime sahiptir ve daha simetriktir: ${\displaystyle (xa)p'_{x}(a,b)+(yb)p'_{y}(a,b)=0}$

${\displaystyle xp'_{x}(a,b)+yp'_{y}(a,b)+p'_{\infty }(a,b)=0,}$

sonsuzda türev nerede . İki denklemin denkliği, P'ye uygulanan Euler'in homojen fonksiyon teoreminden kaynaklanmaktadır . ${\displaystyle p'_{\infty }(x,y)=P'_{z}(x,y,1)}$

Eğer teğet tanımlandığı değildir ve noktası olan tek nokta . ${\displaystyle p'_{x}(a,b)=p'_{y}(a,b)=0,}$

Bu hemen projektif duruma uzanır: P ( x , y , z ) = 0 denkleminin projektif koordinatlarının ( a : b : c ) noktasında tanjantının denklemi

${\displaystyle xP'_{x}(a,b,c)+yP'_{y}(a,b,c)+zP'_{z}(a,b,c)=0,}$

ve tekil olan eğrilerin noktaları öyle noktalardır ki

${\displaystyle P'_{x}(a,b,c)=P'_{y}(a,b,c)=P'_{z}(a,b,c)=0.}$

( P ( a , b , c ) = 0 koşulu, bu koşullar tarafından Euler'in homojen fonksiyon teoremi tarafından ima edilir.)

asimptotlar

Bir cebirsel eğrinin her sonsuz dalı, eğri üzerinde sonsuzdaki bir noktaya, yani eğrinin afin kısmına ait olmayan yansıtmalı tamamlama noktasına karşılık gelir. Karşılık gelen asimptot , o noktadaki eğrinin tanjantıdır. Bir projektif eğriye teğet için genel formül geçerli olabilir, ancak bu durumda bunu açıklığa kavuşturmaya değer.

Izin homojen parçaya bir eğriyi tanımlayan polinom, ayrışma olmak s _ı arasında monomials toplamıdır p derece i . Bunu takip ediyor ${\displaystyle p=p_{d}+\cdots +p_{0}}$

${\displaystyle P={^{h}p}=p_{d}+zp_{d-1}+\cdots +z^{d}p_{0}}$

ve

${\displaystyle P'_{z}(a,b,0)=p_{d-1}(a,b).}$

Eğrinin sonsuzluğundaki bir nokta, ( a , b , 0) biçimindeki p'nin sıfırıdır . Eşdeğer olarak, ( a , b ) p _d' nin sıfırıdır . Cebir temel teoremi bir cebirsel olarak kapalı alan üzerinde, anlamına gelir (tipik olarak, kompleks sayı), s _d doğrusal faktörlerin bir ürün haline faktörler. Her faktör eğri üzerinde sonsuzda bir nokta tanımlar: eğer bx  −  ay böyle bir faktör ise, o zaman sonsuzdaki ( a , b , 0) noktayı tanımlar . Gerçekler üzerinde, p _d faktörleri lineer ve ikinci dereceden faktörlere. İndirgenemez kuadratik faktörler sonsuzda olmayan gerçek noktaları tanımlamak ve gerçek noktaları doğrusal faktörler tarafından verilmiştir. ( a , b , 0) eğrinin sonsuzluğundaki bir noktaysa, ( a , b )'nin asimptotik bir yön olduğu söylenir . Ayar q = p _d karşılık gelen asimptot denklemi

${\displaystyle xq'_{x}(a,b)+yq'_{y}(a,b)+p_{d-1}(a,b)=0.}$

Asimptot sonsuzdaki doğruysa ve gerçek durumda eğrinin bir parabol gibi görünen bir dalı vardır . Bu durumda eğrinin parabolik bir dalı olduğu söylenir . Eğer ${\displaystyle q'_{x}(a,b)=q'_{y}(a,b)=0}$${\displaystyle p_{d-1}(a,b)\neq 0,}$

${\displaystyle q'_{x}(a,b)=q'_{y}(a,b)=p_{d-1}(a,b)=0,}$

eğrinin sonsuzda tekil bir noktası vardır ve birkaç asimptotu olabilir. Tekil bir noktanın teğet konisini hesaplama yöntemiyle hesaplanabilirler.

tekil noktalar

Bir eğrinin tekil noktalar derecesi d polinom ile tanımlanan p ( x , y derecesi) d denklem sisteminin çözeltilerdir:

${\displaystyle p'_{x}(x,y)=p'_{y}(x,y)=p(x,y)=0.}$

Gelen karakteristik sıfır , bu sistem eşdeğerdir

${\displaystyle p'_{x}(x,y)=p'_{y}(x,y)=p'_{\infty }(x,y)=0,}$

burada, önceki bölümün gösterimi ile, Euler'in homojen fonksiyon teoremi nedeniyle sistemler eşdeğerdir . İkinci sistem derecesi üçüncü polinom sahip olma avantajına sahip d -1 yerine d . ${\displaystyle p'_{\infty }(x,y)=P'_{z}(x,y,1).}$

Benzer şekilde, d dereceli homojen bir polinom P ( x , y , z ) ile tanımlanan bir projektif eğri için , tekil noktalar sistemin çözümlerine sahiptir.

${\displaystyle P'_{x}(x,y,z)=P'_{y}(x,y,z)=P'_{z}(x,y,z)=0}$

olarak homojen koordinatlarla . (Pozitif özellikte denklemin sisteme eklenmesi gerekir.) ${\görüntüleme stili P(x,y,z)}$

Bu tekil noktalarının sayısı sonlu sürece olduğunu ima p ( x , y ) ya da P ( x , y , z ) 'dir serbest kare . Bézout'un teoremi , böylece, tekil noktaların sayısının en fazla ( d −1) ² olduğunu ima eder , ancak denklemler sistemi üstbelirlenmiş olduğundan bu sınır keskin değildir . Eğer indirgenebilir polinomları izin verilir, keskin sınırdır d ( d , bu değere ulaşıldığında, -1) / 2 olduğunda eğri birleşimi ise lineer faktörler polinom faktörleri, d hatları. İndirgenemez eğriler ve polinomlar için, tekil noktaların sayısı en fazla ( d −1)( d −2)/2'dir, çünkü formül cinsi tekillikler cinsinden ifade eder (aşağıya bakınız). Maksimuma, tüm tekillikleri çokluk iki ve farklı teğetlere sahip olan sıfır cinsinin eğrileri ile ulaşılır (aşağıya bakınız).

Tekil bir noktadaki teğetlerin denklemi, tekil noktadaki polinomun Taylor serisindeki en düşük derecenin sıfır olmayan homojen kısmı tarafından verilir . Tekil noktayı orijine koymak için koordinatlar değiştirildiğinde, tekil noktadaki teğetlerin denklemi bu nedenle polinomun en düşük derecesinin sıfır olmayan homojen kısmıdır ve tekil noktanın çokluğu bu homojenliğin derecesidir. Bölüm.

analitik yapı

Çalışma analitik yapısı içinde bir cebirsel eğrisinin bölgesinde tekil bir noktasında tekilliklerinden topolojisinin doğru bilgi içerir. Aslında, tekil bir noktanın yakınında, gerçek bir cebirsel eğri, yalnızca tekil noktada kesişen ve bir tepe noktası veya düz bir eğri olarak görünen sonlu sayıda dalın birleşimidir .

Düzenli bir noktanın yakınında, eğrinin koordinatlarından biri, diğer koordinatın analitik bir fonksiyonu olarak ifade edilebilir . Bu, analitik örtük fonksiyon teoreminin bir doğal sonucudur ve eğrinin noktanın yakınında düzgün olduğunu ima eder . Tekil bir noktaya yakın, durum daha karmaşıktır ve dalların analitik parametrik denklemlerini sağlayan Puiseux serisini içerir .

Bir tekilliği tanımlamak için, tekilliği orijinde tutan eğriyi çevirmeye değer . Bu , tekil noktanın koordinatlarının bulunduğu formdaki bir değişken değişikliğinden oluşur . Aşağıda, incelenen tekil noktanın her zaman orijinde olduğu varsayılmaktadır. ${\görüntüleme stili X=xa,Y=yb,}$${\görüntüleme stili a,b}$

Bir cebirsel eğri denklemi f isimli bir polinom içinde x ve y . Bu polinom bir polinom olarak kabul edilebilir y cebirsel kapalı alan katsayıları ile, Puiseux seri olarak x . Böylece f , P'nin bir Puiseux serisi olduğu formun faktörlerinde çarpanlarına ayrılabilir . Eğer bu faktörler birbirinden farklıdır f bir olan indirgenemez polinom bu ima, çünkü f olan kare içermeyen , katsayılar alanında bağımsız bir özellik. ${\görüntüleme stili f(x,y)=0,}$${\görüntüleme stili yP(x),}$

Burada meydana gelen Puiseux serileri şu şekildedir:

${\displaystyle P(x)=\sum _{n=n_{0}}^{\infty }a_{n}x^{n/d},}$

Burada d pozitif bir tamsayıdır ve pozitif olması da varsayılan bir tamsayıdır, çünkü biz sadece eğrinin orijinden geçen dallarını dikkate alıyoruz. Genelliği kaybı olmadan, varsayalım olabilir d olan aralarında asal en büyük ortak bölen ile n böyle (Aksi bir üstler için daha küçük ortak paydayı tercih edebilirsiniz). ${\displaystyle n_{0}}$${\displaystyle a_{n}\neq 0}$

Izin bir olmak ilkel d birlik kök inci . Yukarıdaki Puiseux serisi 'nin çarpanlarına ayrılmasında ortaya çıkarsa , o zaman d serisi ${\ Displaystyle \ omega _{d}}$${\görüntüleme stili f(x,y)=0}$

${\displaystyle P_{i}(x)=\sum _{n=n_{0}}^{\infty}a_{n}\omega _{d}^{i}x^{n/d}}$

çarpanlara ayırmada da meydana gelir ( Galois teorisinin bir sonucu ). Bu d serileri, adı geçen eşleniktir ve dallanma indeksi d' nin eğrisinin tek bir dalı olarak kabul edilir .

Gerçek katsayılı bir polinom tarafından tanımlanan bir eğri olan gerçek bir eğri söz konusu olduğunda, üç durum ortaya çıkabilir. Hiçbirinin gerçek katsayıları yoksa , birinin gerçek olmayan bir dalı vardır. Bazılarının gerçek katsayıları varsa, o zaman olarak seçilebilir . Eğer d garip, o zaman her gerçek değeri x gerçek bir değer sağlar ve eğer tekil olmasına rağmen biri, o bakışlar düzenli bir gerçek şubesi vardır d > 1 . Eğer d bile, daha sonra ve fakat yalnızca, gerçek değerlere sahip x ≥ 0 . Bu durumda, gerçek dal bir tepe noktası olarak görünür (veya kullanılan bir tepe noktasının tanımına bağlı olarak bir tepe noktasıdır). ${\görüntüleme stili P_{i}(x)}$${\görüntüleme stili P_{i}(x)}$${\görüntüleme stili P_{0}(x)}$${\görüntüleme stili P_{0}(x)}$${\görüntüleme stili P_{0}(x)}$${\görüntüleme stili P_{d/2}(x)}$

Örneğin, sıradan bir tepe noktasının yalnızca bir dalı vardır. Denklem tarafından tanımlanırsa , çarpanlara ayırma, dallanma indeksi 2'dir ve iki faktör gerçektir ve her biri yarım dal tanımlar. Tepe noktası döndürülürse, denklem olur ve çarpanlara ayırma ile olur ( yukarıdaki tanımın nasıl özelleştiğini göstermek için katsayı j'ye sadeleştirilmemiştir ). Burada dallanma indeksi 3'tür ve sadece bir faktör gerçektir; bu, ilk durumda, iki faktörün aynı dalı tanımlıyor gibi düşünülmesi gerektiğini göstermektedir. ${\displaystyle y^{2}-x^{3}=0,}$${\displaystyle (yx^{3/2})(y+x^{3/2});}$${\displaystyle y^{3}-x^{2}=0,}$${\displaystyle (yx^{2/3})(yj^{2}x^{2/3})(y-(j^{2})^{2}x^{2/3}),}$${\displaystyle j=(1+{\sqrt {-3}})/2}$${\ Displaystyle (j^{2})^{2}}$${\görüntüleme stili P_{i}(x)}$

Düzlem olmayan cebirsel eğriler

Bir cebirsel eğri bir bir cebirsel çeşitli arasında boyut on. Bu, n boyutlu bir afin uzayda afin bir eğrinin , n değişkende en az n- 1 polinom tarafından tanımlandığı anlamına gelir . Bir eğri tanımlamak için şu polinomları bir oluşturmalıdır asal ideali arasında Krull boyutu Bu durum pratikte test etmek kolay değildir 1.. Bu nedenle, düzlem olmayan eğrileri temsil etmek için aşağıdaki yol tercih edilebilir.

Izin olması , n iki değişken polinomları x ₁ ve x ₂ , öyle ki ön indirgenemez. Koordinatları denklemleri ve eşitsizlikleri sağlayan n boyutunun afin uzayındaki noktalar${\displaystyle f,g_{0},g_{3},\ldots ,g_{n}}$

${\displaystyle {\begin{aligned}&f(x_{1},x_{2})=0\\&g_{0}(x_{1},x_{2})\neq 0\\x_{3}& ={\frac {g_{3}(x_{1},x_{2})}{g_{0}(x_{1},x_{2})}}\\&{}\ \vdots \\x_ {n}&={\frac {g_{n}(x_{1},x_{2})}{g_{0}(x_{1},x_{2})}}\end{aligned}}}$

sonlu sayıda noktanın kaldırıldığı bir cebirsel eğrinin tüm noktalarıdır. Bu eğri, polinomları ideali jeneratör sistemi tarafından tanımlanır h bir tamsayıdır bulunacak şekilde k gibi üretilen ideale ait . Bu temsil, eğri ile f tarafından tanımlanan düzlem eğrisi arasındaki çift ​​yönlü bir denkliktir . Her cebirsel eğri bu şekilde temsil edilebilir. Bununla birlikte, ilk iki değişken üzerindeki projeksiyonu hemen hemen her zaman dolaylı hale getirmek için değişkenlerin doğrusal bir değişimine ihtiyaç duyulabilir . Değişkenlerin değiştirilmesi gerektiğinde, hemen hemen her değişiklik, sonsuz bir alan üzerinde tanımlandığı anda uygundur. ${\displaystyle g_{0}^{k}h}$${\displaystyle f,x_{3}g_{0}-g_{3},\ldots ,x_{n}g_{0}-g_{n}}$

Bu temsil, grafik gösterimi de dahil olmak üzere, düzlemsel olmayan bir cebirsel eğrinin herhangi bir özelliğini, düzlem izdüşümünün karşılık gelen özelliğinden kolayca çıkarmamızı sağlar.

Örtük denklemleriyle tanımlanan bir eğri için, eğrinin yukarıdaki temsili , daha küçük değişkenlerin bloğu ( x ₁ , x ₂ ) olacak şekilde bir blok sıralaması için bir Gröbner temelinden kolayca çıkarılabilir . Polinom f , yalnızca x ₁ ve x _2'ye bağlı olan tabandaki benzersiz polinomdur . Fraksiyonlar g _i / g ₀ için, seçerek elde edilir i 3, ..., = N , esas olarak bir polinom doğrusal olduğunu x _i sadece bağlıdır x ₁ , x ₂ ve x _i . Bu seçimler mümkün değilse, bu ya denklemlerin çeşitlilik olmayan bir cebirsel kümeyi tanımladığı ya da çeşitliliğin birinci boyutta olmadığı ya da koordinatların değişmesi gerektiği anlamına gelir. İkinci durum, f var olduğunda ve benzersiz olduğunda ortaya çıkar ve i = 3, ..., n için , baştaki tek terimli yalnızca x ₁ , x ₂ ve x _i'ye bağlı olan polinomlar vardır .

Cebirsel fonksiyon alanları

Cebirsel eğrilerin incelenmesi, indirgenemez cebirsel eğrilerin çalışmasına indirgenebilir : iki küçük eğrinin birleşimi olarak yazılamayan eğriler. Kadar birational denklik, bir alanın üzerine indirgenemez eğriler F vardır kategorik eşdeğer için fonksiyon cisimleri üzerinde bir değişkende F . Bu tür bir cebirsel işlev alanı olan cisim genişlemesi K arasında F bir eleman içeren , x olduğu aşkın fazla F , ve bu şekilde K sonlu cebirsel uzantısıdır F ( x belirsiz rasyonel fonksiyonların alandır), x üzerinde  F .

Örneğin, alan dikkate C biz alan tanımlayabilir, üzerinde karmaşık sayılar, C ( X rasyonel fonksiyonların)  C . Eğer y ²  =  x ³  -  X  - 1, daha sonra alan Cı ( x ,  y ), bir bir eliptik işlev alanı . x öğesi benzersiz olarak belirlenmemiştir; alan, örneğin, C ( y )' nin bir uzantısı olarak da kabul edilebilir . Fonksiyon alanına tekabül eden cebirsel eğri sadece nokta grubudur ( x ,  y olarak) C ² tatmin y ²  =  x ³  -  X  - 1.

Eğer F alanı cebirsel olarak kapalı değilse, fonksiyon alanlarının bakış açısı, noktaların yerini dikkate almaktan biraz daha geneldir, çünkü örneğin üzerlerinde hiçbir noktası olmayan "eğrileri" dahil ederiz. Taban alanı, örneğin, F alanı olan R, gerçek sayılar, daha sonra x ²  +  y ²  = -1 cebirsel uzatma alanı tanımlar R ( x ), ancak bir alt kümesi olarak kabul karşılık gelen eğri R ² bir noktaları vardır . Denklemi x ²  +  y ²  = -1 fazla indirgenemez cebirsel eğri tanımlıyor R de şema duyu (bir integrali , ayrılmış tek boyutlu düzenleri arasında sonlu türü üzerinde R ). Bu anlamda, fazla indirgenemez cebirsel eğriler arasında bire bir karşılık F üzerinde bir değişken (yukarı birational denklik için) ve cebirsel fonksiyon alanları F , genel olarak tutar.

İki eğri, eğriler olarak izomorfik olmadan çift ​​yönlü olarak eşdeğer olabilir (yani izomorfik fonksiyon alanlarına sahip olabilir). Tekil olmayan eğrilerle, yani herhangi bir tekilliği olmayan eğrilerle uğraşırken durum daha kolay hale gelir . Bir alan üzerindeki iki tekil olmayan yansıtmalı eğri, ancak ve ancak onların fonksiyon alanları eşbiçimliyse izomorfiktir.

Tsen teoremi , cebirsel olarak kapalı bir alan üzerindeki cebirsel eğrinin fonksiyon alanı ile ilgilidir.

Karmaşık eğriler ve gerçek yüzeyler

Karmaşık bir yansıtmalı cebirsel eğri, n -boyutlu karmaşık yansıtmalı uzayda CP ^{n bulunur} . Bu kompleks boyuta sahip n gerçek olarak değil, topolojik bir boyut, manifold , 2 n , ve bir kompakt , bağlı ve yönlendirilebilir . C üzerindeki bir cebirsel eğri de benzer şekilde iki topolojik boyuta sahiptir; başka bir deyişle, bir yüzeydir .

Topolojik cinsi kolları ya da halka delik sayısı, bu yüzey, bir eşittir geometrik cinsi cebirsel vasıtasıyla hesaplanabilir cebirsel eğrisi. Kısacası, d derecesine ve yalnızca adi tekilliklere (farklı tanjantlara sahip iki çokluk tekillikleri) sahip tekil olmayan bir eğrinin düzlem izdüşümü düşünülürse , o zaman cins ( d  − 1)( d  − 2)/2 −  k , burada k bu tekilliklerin sayısıdır.

Kompakt Riemann yüzeyleri

Bir Riemann yüzeyi , onu iki boyutlu bir bağlantılı gerçek manifold yapan, bir karmaşık boyutun bağlı bir karmaşık analitik manifoldudur. Öyle kompakt bir topolojik uzay olarak kompakt olup olmadığını.

C üzerinde düzgün indirgenemez projektif cebirsel eğriler kategorisi (morfizmler olarak sabit olmayan düzenli haritalar ile ), kompakt Riemann yüzeyleri kategorisi ( morfizmler olarak sabit olmayan holomorfik haritalar ile ) ve bunun tersi arasında üçlü bir kategori denkliği vardır . C üzerinde bir değişkendeki cebirsel fonksiyon alanlarının kategorisi ( C'yi morfizmler olarak sabitleyen alan homomorfizmaları ile ). Bu, bu üç konuyu incelerken bir anlamda bir ve aynı şeyi inceliyoruz demektir. Cebirsel geometride karmaşık analitik yöntemlerin, karmaşık analizlerde cebirsel-geometrik yöntemlerin ve her ikisinde de alan teorik yöntemlerin kullanılmasına izin verir. Bu, cebirsel geometride çok daha geniş bir problem sınıfının özelliğidir.

Daha genel bir teori için ayrıca cebirsel geometri ve analitik geometriye bakın.

tekillikler

İntrinsik kavram kullanılarak teğet alanı , noktalar P bir cebirsel eğrisinin C olarak sınıflandırılan düz (: ayn tekil olmayan ), ya da başka Tekil . n +1 değişkenli n -1 homojen polinomlar verildiğinde , Jacobian matrisini kısmi türevlerin ( n −1)×( n +1) matrisi olarak bulabiliriz. Eğer sıra bu matrisin olup , n 1, o zaman polinomlar (aksi takdirde yüksek boyutun bir cebirsel çeşitli tanımlamak) cebirsel eğri tanımlar. Jacobian matrisi eğri üzerindeki bir P noktasında değerlendirildiğinde rank n -1 olarak kalırsa , nokta düzgün veya düzenli bir noktadır; aksi halde tekil bir noktadır . Özellikle, eğer eğri tek bir homojen polinom denklemi f ( x , y , z ) = 0 ile tanımlanan bir düzlem yansıtmalı cebirsel eğri ise , o zaman tekil noktalar tam olarak P noktalarıdır ve burada 1×( n + 1) matris sıfırdır, yani

${\displaystyle {\frac {\kısmi f}{\kısmi x}}(P)={\frac {\kısmi f}{\kısmi y}}(P)={\frac {\kısmi f}{\kısmi z}}(P)=0.}$

Yana f bir polinomdur bu tanım cebirsel ve alan doğası hakkında hiçbir varsayım yapar F özellikle gerek gerçek veya karmaşık sayılar vermeye. Elbette (0,0,0)'nin eğrinin bir noktası olmadığı ve dolayısıyla tekil bir nokta olmadığı unutulmamalıdır.

Benzer şekilde, tek bir polinom denklemi f ( x , y ) = 0 ile tanımlanan bir afin cebirsel eğri için , tekil noktalar tam olarak 1× n Jacobian matrisinin rankının sıfır olduğu eğrinin P noktalarıdır , yani, nerede

${\displaystyle f(P)={\frac {\kısmi f}{\kısmi x}}(P)={\frac {\kısmi f}{\kısmi y}}(P)=0.}$

Bir eğrinin tekillikleri çift yönlü değişmezler değildir. Bununla birlikte, bir eğrinin tekilliklerini bulmak ve sınıflandırmak, çift yönlü değişmez olan cinsi hesaplamanın bir yoludur . Bunun çalışması için, eğriyi yansıtmalı olarak ele almalı ve F'nin cebirsel olarak kapalı olmasını talep etmeliyiz , böylece eğriye ait tüm tekillikler dikkate alınır.

Tekilliklerin sınıflandırılması

Tekil noktalar, eğrinin kendi üzerinden geçtiği çoklu noktaları ve ayrıca çeşitli cusp türlerini içerir , örneğin ( 0,0'da x ³  = y ² denklemiyle eğri tarafından gösterilenler ).

Bir C eğrisinin en fazla sonlu sayıda tekil noktası vardır. Hiçbiri yoksa, düzgün veya tekil olmayan olarak adlandırılabilir . Genellikle, bu tanım cebirsel olarak kapalı bir alan üzerinden ve projektif uzayda bir C eğrisi için anlaşılır (yani, cebirsel geometri anlamında tam ). Örneğin, denklemin düzlem eğrisi , sonsuzda tekil bir noktaya (bir tepe noktası) sahip olduğu için tekil olarak kabul edilir. ${\displaystyle yx^{3}=0}$

Bu bölümün geri kalanında, iki değişkenli bir polinom f ( x , y ) sıfır kümesi olarak tanımlanan bir düzlem eğrisi C ele alınır . Sonuçların tümü olmasa da bazıları düzlemsel olmayan eğrilere genelleştirilebilir.

Tekil noktalar birkaç değişmez vasıtasıyla sınıflandırılır. Çokluğu m, örneğin tam sayı fazla olarak tanımlanır türevleri f kadar tüm siparişler için m - 1 vanish (aynı zamanda en az kesişim sayısı eğrisine ve bir düz çizgi arasındaki P ). Sezgisel olarak, tekil bir noktanın delta değişmezi vardır δ eğer yoğunlaşıyorsa δ P noktasında sıradan çift noktalar . Bu hassas hale getirmek için, yukarı üfleme işlemi olarak adlandırılan üretir sonsuz yakın noktası ve toplanmasıyla m ( m -1) / 2 sonsuz yakın noktalardan, fazla m kendi çokluğu olan üretir Í . İndirgenemez ve indirgenmiş bir eğri ve bir P noktası için δ'yi cebirsel olarak yerel halkanın P'de nerede olduğu ve onun integral kapanışı olarak tanımlayabiliriz . ${\displaystyle {\widetilde {{\mathcal {O}}_{P}}}/{\mathcal {O}}_{P}}$${\görüntüleme stili {\matematiksel {O}}_{P}}$${\ Displaystyle {\widetilde {{\mathcal {O}}_{P}}}}$

Milnor numarası μ bir tekillik haritalama derecesidir derece f ( x , y )/|derece  f ( x , y )|topolojik anlamında yarıçapı £ değerinin küçük küre üzerinde sürekli bir eşleme derecesi , grad  f (kompleksleri), gradyan vektörü alandır f . Bu ö ve ilgilidir r ile Milnor-Jung formül ,

μ = 2δ − r + 1.

Burada, dallanma sayısı r ve P lokal indirgenemez dalların sayısı P . Örneğin, R = 1 sıradan cups'daki ve r = 2 sıradan bir çift nokta. m çokluğu en az r'dir ve P , ancak ve ancak m en az 2 ise tekildir . Ayrıca, δ en az m ( m -1)/2'dir.

Tüm tekilliklerin delta değişmezlerini hesaplamak, eğrinin g cinsinin belirlenmesini sağlar; Eğer d sonra, derece

${\displaystyle g={\frac {1}{2}}(d-1)(d-2)-\sum _{P}\delta _{P},}$

burada toplam, karmaşık projektif düzlem eğrisinin tüm tekil noktaları P üzerinden alınır . Cins formülü denir .

Değişmezleri [ m , δ, r ] bir tekilliğe atayın , burada m çokluk, δ delta-değişmez ve r dallanma sayısıdır. O zaman sıradan bir tepe noktası, [2,1,1] değişmezleri olan bir noktadır ve sıradan bir çift nokta , [2,1,2] değişmezleri olan bir noktadır ve sıradan bir m -çoklu noktası, değişmezleri [ m , m ] olan bir noktadır. ( m −1)/2, m ].

Eğri örnekleri

rasyonel eğriler

Bir rasyonel eğrisi da unicursal eğrisi adı, herhangi bir eğridir birationally eşdeğer bir yansıtmalı hattı olarak alabilir bir hat için; buna göre, eğrinin fonksiyon alanını, bir belirsiz F ( x ) içindeki rasyonel fonksiyonların alanı ile tanımlayabiliriz . Eğer F cebirsel kapalı olduğu, bu bir eğri eşdeğerdir cinsi sıfır; ancak, x ² + y ²  = -1 gerçek cebirsel çeşidinde tanımlanan tüm gerçek cebirsel fonksiyonların alanı, rasyonel bir fonksiyon alanı olmayan sıfır cinsinin bir alanıdır.

Somut olarak, boyutu n bölü F olan bir afin uzayda gömülü rasyonel bir eğri, tek bir parametrenin n rasyonel fonksiyonu aracılığıyla (izole istisnai noktalar hariç) parametreleştirilebilir t ; Aynı payda bu rasyonel fonksiyonlar azaltarak, n + 1 elde edilen polinomlar tanımlamak polinom parametrizasyonunu ait yansıtmalı tamamlanması yansıtmalı alan eğrisinin. Bir örneği, rasyonel normal eğri bu polinomlar olan monomials .

Herhangi bir konik bölüm üzerinden tanımlanan F bir ile rasyonel noktası olarak F rasyonel bir eğridir. Rasyonel noktadan t eğimli bir çizgi çizerek ve düzlem ikinci dereceden eğri ile bir kesişim yaparak parametreleştirilebilir ; bu, F- rasyonel katsayıları ve bir F- rasyonel kökü olan bir polinom verir , dolayısıyla diğer kök de F- rasyoneldir (yani, F'ye aittir ).

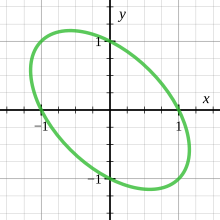
Örneğin, x ² + xy + y ²  = 1 elipsini ele alalım, burada (-1, 0) rasyonel bir noktadır. (−1,0), y  = t ( x +1) den eğimi t olan bir doğru çizerek, onu elips denkleminde yerine koyarak, çarpanlara ayırarak ve x için çözerek elde ederiz.

${\displaystyle x={\frac {1-t^{2}}{1+t+t^{2}}}.}$

Daha sonra denklemi y olan

${\displaystyle y=t(x+1)={\frac {t(t+2)}{1+t+t^{2}}}\,,}$

bu, elipsin rasyonel bir parametreleştirilmesini tanımlar ve dolayısıyla elipsin rasyonel bir eğri olduğunu gösterir. t  = ∞'ye karşılık gelen (-1,1) hariç, elipsin tüm noktaları verilmiştir ; tüm eğri bu nedenle gerçek yansıtmalı çizgi ile parametrelenir.

Böyle bir rasyonel parametreleştirme, projektif uzayda , ilk projektif koordinatları parametreleştirmenin paylarına ve sonuncusunu ortak paydaya eşitleyerek düşünülebilir. Parametre projektif bir satırda tanımlandığı için parametredeki polinomlar homojenleştirilmelidir . Örneğin, yukarıdaki elipsin projektif parametreleştirilmesi,

${\displaystyle X=U^{2}-T^{2},\quad Y=T\,(T+2\,U),\quad Z=T^{2}+TU+U^{2} .}$

Bu denklemler arasında T ve U'yu ortadan kaldırarak tekrar elipsin projektif denklemini elde ederiz.

${\displaystyle X^{2}+X\,Y+Y^{2}=Z^{2},}$

bu, yukarıdaki denklemin homojenleştirilmesiyle doğrudan elde edilebilir.

Wikipedia'nın eğriler listesindeki eğrilerin çoğu rasyoneldir ve bu nedenle benzer rasyonel parametreleştirmelere sahiptir.

Rasyonel düzlem eğrileri

Rasyonel düzlem eğrileri, içine gömülü rasyonel eğrilerdir . İki koordinatta derece homojen polinomların genel bölümleri verildiğinde , bir harita var${\displaystyle \mathbb {P} ^{2}}$${\displaystyle s_{1},s_{2},s_{3}\in \Gamma (\mathbb {P} ^{1},{\mathcal {O}}(d))}$${\görüntüleme stili d}$${\görüntüleme stili x,y}$

${\displaystyle s:\mathbb {P} ^{1}\to \mathbb {P} ^{2}}$ tarafından verilen ${\displaystyle s([x:y])=[s_{1}([x:y]):s_{2}([x:y]):s_{3}([x:y])]}$

dereceli bir rasyonel düzlem eğrisi tanımlama . Tüm bu tür kararlı eğrileri parametrelendiren ilişkili bir modül uzayı (burada hiperdüzlem sınıfı) vardır . Modül boşlukları boyutunu belirlemek için bir boyut sayımı yapılabilir: Her bir kesit için toplam parametre verilmesinde parametreler vardır. Onlar yansıtmalı bölüm kadar kabul edilir çünkü Sonra, içinde olduğu daha az parametre . Ayrıca, üç boyutlu bir otomorfizm grubu vardır , dolayısıyla boyutu vardır . Bu modül uzayı, Gromov-Witten teorisi kullanılarak kesişen noktaların dereceli rasyonel düzlem eğrilerinin sayısını saymak için kullanılabilir . Özyinelemeli bağıntı tarafından verilir${\görüntüleme stili d}$ ${\displaystyle {\mathcal {M}}={\overline {\mathcal {M}}}_{0,0}(\mathbb {P} ^{2},d\cdot [H])}$${\görüntüleme stili [H]}$${\ Displaystyle d+1}$${\displaystyle \Gamma (\mathbb {P} ^{1},{\mathcal {O}}(d))}$${\ Displaystyle 3d+3}$${\displaystyle \mathbb {P} ^{2}}$${\görüntüleme stili 1}$${\görüntüleme stili {\matematiksel {M}}}$${\displaystyle \mathbb {P} ^{1}}$${\görüntüleme stili {\matematiksel {M}}}$${\ Displaystyle 3d+3-1-3=3d-1}$${\ Displaystyle N_{d}}$${\görüntüleme stili d}$${\ Displaystyle 3d-1}$

${\displaystyle N_{d}=\sum _{d_{A}+d_{B}=d}N_{d_{A}}N_{d_{B}}d_{A}^{2}d_{B} \left(d_{B}{\binom {3d-4}{3d_{A}-2}}-d_{A}{\binom {3d-4}{3d_{A}-1}}\sağ)}$

nerede . ${\displaystyle N_{1}=N_{2}=1}$

eliptik eğriler

Bir eliptik eğri arasında herhangi bir eğri olarak tanımlanabilir cinsi bir ile bir rasyonel noktası : ortak bir model tekil olmayan kübik eğrisi her cins bir eğri model yeterli. Bu modelde, ayırt edici nokta genellikle sonsuzluktaki bir bükülme noktası olarak alınır; bu, eğrinin projektif versiyonunda Tate-Weierstrass biçiminde yazılabilmesini gerektirir.

${\displaystyle y^{2}z+a_{1}xyz+a_{3}yz^{2}=x^{3}+a_{2}x^{2}z+a_{4}xz^{ 2}+a_{6}z^{3}.}$

Alanın karakteristiği 2 ve 3'ten farklıysa, o zaman doğrusal bir koordinat değişikliği , klasik Weierstrass formunu veren koymaya izin verir. ${\displaystyle a_{1}=a_{2}=a_{3}=0,}$

${\displaystyle y^{2}=x^{3}+px+q.}$

Eliptik eğriler , grup yasasının kimliği olarak ayırt edici nokta ile değişmeli bir grubun yapısını taşır . Düzlemsel bir kübik modelde, gruptaki üç noktanın toplamı, ancak ve ancak eşdoğrusal olmaları durumunda sıfıra eşittir . Karmaşık sayılar üzerinde tanımlanan bir eliptik eğri için grup, ilgili eliptik fonksiyonların periyot kafesi modulo karmaşık düzleminin toplama grubuna eşbiçimlidir .

İki kuadrik yüzeyin kesişimi, genel olarak, cins bir ve derece dört olan tekil olmayan bir eğridir ve dolayısıyla rasyonel bir noktası varsa, eliptik bir eğridir. Özel durumlarda, kesişim ya rasyonel tekil bir kuartik olabilir ya da her zaman farklı olmayan daha küçük dereceli eğrilerde ayrıştırılır (bir kübik eğri ve bir çizgi veya iki konik veya bir konik ve iki çizgi veya dört çizgi) .

Birden büyük cins eğrileri

Eğrileri cinsi birden büyük hem de rasyonel ve eliptik eğri oldukça farklıdırlar. Faltings teoremi tarafından rasyonel sayılar üzerinde tanımlanan bu tür eğriler , yalnızca sonlu sayıda rasyonel noktaya sahip olabilir ve hiperbolik bir geometri yapısına sahip olarak görülebilirler . Örnekler, hipereliptik eğriler , Klein kuartik eğrisi ve n üçten büyük olduğunda Fermat eğrisi x ⁿ  +  y ⁿ  = z ^n'dir . Ayrıca projektif düzlem eğrileri ve içindeki eğriler birçok faydalı örnek sağlar. ${\displaystyle \mathbb {P} ^{2}}$${\displaystyle \mathbb {P} ^{1}\times \mathbb {P} ^{1}}$

Projektif düzlem eğrileri

Bir jenerik kesitin kaybolan yeri olarak oluşturulabilen düzlemsel derece eğrileri , cinse sahiptir.${\displaystyle C\subset \mathbb {P} ^{2}}$${\görüntüleme stili k}$${\displaystyle s\in \Gamma (\mathbb {P} ^{2},{\mathcal {O}}(k))}$

${\displaystyle {\frac {(k-1)(k-2)}{2}}}$

Bu, Tutarlı demet kohomolojisi kullanılarak hesaplanabilir . Derecelerine göre eğri türlerinin kısa bir özetini burada bulabilirsiniz.

${\displaystyle {\begin{matrix}{\text{derece}}&1&2&3&4&5&6&7\{\text{cins}}&0&0&1&3&6&10&15\end{matrix}}}$

Örneğin, eğri cinsinin bir eğri tanımlar olan düz diferansiyel çünkü genel bir bölümü olmayan bir örneği, bir eğri .. ile ortak sıfır olması eğrisidir ile teoremi Bezouts , en kesişmelidir sayı, olduğu iki noktada kesişen iki rasyonel eğrinin birleşimi. Not , öğesinin kaybolan yeri tarafından verilir ve öğesinin kaybolan yeri tarafından verilir . Bunlar açıkça bulunabilir: her ikisinde de bir nokta bulunur if . Yani iki çözüm öyle noktalardır ki , olan ve . ${\displaystyle x^{4}+y^{4}+z^{4}}$${\görüntüleme stili 3}$${\displaystyle 4x^{3},4y^{3},4z^{3}}$${\displaystyle x(x^{2}+y^{2}+z^{2})}$${\görüntüleme stili 2}$${\displaystyle C_{1}\cup C_{2}}$${\görüntüleme stili C_{1}}$${\görüntüleme stili x}$${\ Displaystyle C_{2}}$${\displaystyle x^{2}+y^{2}+z^{2}}$${\görüntüleme stili x=0}$${\görüntüleme stili [0:y:z]}$${\displaystyle y^{2}+z^{2}=0}$${\görüntüleme stili [0:1:-1]}$${\displaystyle [0:1:{\sqrt {-1}}]}$

Projektif çizgilerin çarpımındaki eğriler

Kaybolan yeri tarafından verilen eğri , for , cinsinin eğrilerini verir${\displaystyle C\subset \mathbb {P} ^{1}\times \mathbb {P} ^{1}}$${\displaystyle s\in \Gamma (\mathbb {P} ^{1}\times \mathbb {P} ^{1},{\mathcal {O}}(a,b))}$${\displaystyle a,b\geq 2}$

${\displaystyle ab-a-b+1}$

Tutarlı demet kohomolojisi kullanılarak kontrol edilebilir . Eğer , o zaman cinsin eğrilerini tanımlarlarsa , dolayısıyla herhangi bir cinsin bir eğrisi içinde bir eğri olarak oluşturulabilir . Cinsleri tabloda özetlenebilir${\görüntüleme stili a=2}$${\ Displaystyle 2b-2-b+1=b-1}$${\displaystyle \mathbb {P} ^{1}\times \mathbb {P} ^{1}}$

${\displaystyle {\begin{matrix}{\text{bidegree}}&(2,2)&(2,3)&(2,4)&(2,5)\\{\text{cins}}&1&2&3&4 \end{matris}}}$

ve için , bu${\görüntüleme stili a=3}$

${\displaystyle {\begin{matrix}{\text{bidegree}}&(3,2)&(3,3)&(3,4)&(3,5)\\{\text{cins}}&2&4&6&8 \end{matris}}}$

Ayrıca bakınız

Klasik cebirsel geometri

Modern cebirsel geometri

Riemann yüzeylerinin geometrisi

Notlar

Referanslar

• Brieskorn, Egbert; Knorrer, Horst (2013). Düzlem Cebirsel Eğriler . Stillwell, John Çeviren. Birkhäuser. ISBN'si 978-3-0348-5097-1.
• Chevalley, Claude (1951). Tek Değişkenli Cebirsel Fonksiyonlar Teorisine Giriş . Matematiksel anketler. 6 . Amerikan Matematik Derneği. ISBN'si 978-0-8218-1506-9.
• Coolidge, Julian L. (2004) [1931]. Cebirsel Düzlem Eğrileri Üzerine Bir İnceleme . Dover. ISBN'si 978-0-486-49576-7.
• Farkas, HM; Kra, I. (2012) [1980]. Riemann Yüzeyleri . Matematikte Lisansüstü Metinler. 71 . Springer. ISBN'si 978-1-4684-9930-8.
• Fulton, William (1989). Cebirsel Eğriler: Cebirsel Geometriye Giriş . Matematik ders notu serisi. 30 (3. baskı). Addison-Wesley. ISBN'si 978-0-201-51010-2.
• Gibson, CG (1998). Cebirsel Eğrilerin Temel Geometrisi: Bir Lisans Girişi . Cambridge Üniversitesi Yayınları. ISBN'si 978-0-521-64641-3.
• Griffiths, Phillip A. (1985). Cebirsel Eğrilere Giriş . Matematiksel Monografların Tercümesi. 70 (3. baskı). Amerikan Matematik Derneği. ISBN'si 9780821845370.
• Hartshorne, Robin (2013) [1977]. Cebirsel Geometri . Matematikte Lisansüstü Metinler. 52 . Springer. ISBN'si 978-1-4757-3849-0.
• Iitaka, Shigeru (2011) [1982]. Cebirsel Geometri: Cebirsel Çeşitlerin Birational Geometrisine Giriş . Matematikte Lisansüstü Metinler. 76 . Springer New York. ISBN'si 978-1-4613-8121-1.
• Milnor, John (1968). Karmaşık Hiperyüzeylerin Tekil Noktaları . Princeton Üniversitesi Yayınları. ISBN'si 0-691-08065-8.
• Serre, Jean-Pierre (2012) [1988]. Cebirsel Gruplar ve Sınıf Alanları . Matematikte Lisansüstü Metinler. 117 . Springer. ISBN'si 978-1-4612-1035-1.
• Kötter, Ernst (1887). "Grundzüge einer rein geometrischen Theorie der algebraischen ebenen Eğrisi" [ Cebir düzlem eğrilerinin tamamen geometrik bir teorisinin temelleri]. Berlin Kraliyet Akademisi'nin İşlemleri . - 1886 Akademi ödülünü kazandı