Kare üçgen sayı - Squared triangular number

Kenar uzunluğu üçgen bir sayı olan bir kare karelere ve alanları küplere eklenen yarım karelere bölünebilir. Gönderen (2010) Gulley .

Gelen sayı teorisi , birinci toplamı $, n$ küp olan kare ve $n$ inci üçgen sayıda . Yani,

1^{3}+2^{3}+3^{3}+\cdots +n^{3}=\left(1+2+3+\cdots +n\sağ)^{2} .

Aynı denklem, toplama için matematiksel gösterim kullanılarak daha kompakt bir şekilde yazılabilir :

\sum _{k=1}^{n}k^{3}={\bigg (}\sum _{k=1}^{n}k{\bigg )}^{2}.

Bu özdeşliğe bazen, Gerasa'lı Nicomachus'tan (c. 60 – c. 120 CE) sonra, Nicomachus'un teoremi denir .

Tarih

Nicomachus, Aritmetiğe Giriş kitabının 20. Bölümünün sonunda , tek sayıların bir listesi yazılırsa, ilkinin 1'in küpü, sonraki ikisinin toplamının 2'nin küpü, toplamının 2'nin küpü olduğuna dikkat çekti. sonraki üç, 3'ün küpüdür, vb. Bundan daha ileri gitmez, ancak bundan ilk $n$ küpün toplamının ilk tek sayıların, yani 1'den 'ye kadar olan tek sayıların toplamına eşit olduğu sonucu çıkar . Bu sayıların ortalaması açıktır ve onlardan vardır, yani toplamları $n(n+1)/2$ ${\ Displaystyle n(n+1)-1}$ $n(n+1)/2$ $n(n+1)/2$ ${\bigl (}n(n+1)/2{\bigr )}^{2}.$

Birçok erken matematikçi, Nicomachus teoreminin kanıtlarını inceledi ve sağladı. Stroeker (1995) , "sayı teorisinin her öğrencisinin kesinlikle bu mucizevi gerçeğe hayret etmiş olması gerektiğini" iddia eder. Pengelley (2002) kimlik başvurular bulur sadece eserlerinde Nicomachus şimdi ne de Ürdün birinci yüzyılda CE, aynı zamanda içinde olanlarda Aryabhata içinde Hindistan , beşinci yüzyılda ve bu içinde El-Kerecî 1000 yıllarından içinde İran . Bressoud (2004) , bu formül üzerine Al-Qabisi (onuncu yüzyıl Arabistan), Gersonides (yaklaşık 1300 Fransa) ve Nilakantha Somayaji (yaklaşık 1500 Hindistan); Nilakantha'nın görsel kanıtını yeniden üretiyor.

Sayısal değerler; geometrik ve olasılıksal yorumlama

3×3 kare (4×4) içinde 14 [ 1 ² + 2 ² + 3 ² ] kare (kırmızı) dahil 36 [ (1 + 2 + 3) ² = 1 ³ + 2 ³ + 3 ³ ] dikdörtgenin tümü köşe) ızgarası

Kare üçgen sayıların dizisi

0, 1, 9, 36, 100, 225,

441, 784, 1296, 2025, 3025, 4356, 6084, 8281,

... .

Bu sayılar , üçgen sayıların ve kare piramidal sayıların dört boyutlu hiperpiramidal bir genellemesi olan şekilsel sayılar olarak görülebilir .

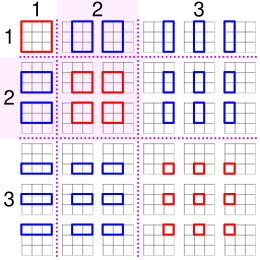
Olarak Stein (1971) gözlemler, bu sayılar da içinde oluşturulan yatay ve dikey kenarları olan dikdörtgenleri sayısını $n x n$ ızgara . Örneğin, $4 \times 4$ ızgaranın (veya bir kenardaki üç küçük kareden oluşan bir karenin) noktaları 36 farklı dikdörtgen oluşturabilir. Kare bir ızgaradaki karelerin sayısı benzer şekilde kare piramidal sayılarla sayılır.

Özdeşlik ayrıca aşağıdaki gibi doğal bir olasılık yorumunu da kabul eder. Let $X, Y, Z,, W,$ bağımsız bir şekilde, ve muntazam biçimde rastgele seçilen dört tam sayıları olarak $1$ ve $n$ . O halde, $W'nin$ dört sayının en büyüğü olma olasılığı, $Y'nin$ en az $X kadar$ ve $W'nin$ de en az $Z$ kadar büyük olma olasılığına eşittir . Yani, . Herhangi bir değeri için, $W$ , kombinasyonları $X$ , $Y$ ve $Z$ yapmak $W$ büyük şeklinde bir küp $1 \leq$ $X$ $,$ $Y$ $,$ $Z,$ $\leq$ $n$ böylece (tüm seçenekleri üzerinde bu küp büyüklüğü ilave $W$ kombinasyonlarının sayısı) ve $X$ $,$ $Y,$ $,$ $Z$ $,$ $W$ olan $W$ büyük olan küpler bir toplamı, Nichomachus kimlik sol tarafıdır. Çiftleri de $($ $X$ $,$ $Y$ $)$ ile $X-$ $\leq$ $Y$ ve çiftleri $($ $Z$ $,$ $W$ $)$ ile $Z$ $\leq$ $B$ formu doğru üçgen, ikizkenar, ve olasılıkları denklemin sağ tarafına tarafından sayılan dizi Kartezyen ürün bunlardan iki üçgen, yani boyutu, Nichomachus kimliğinin sağ tarafındaki üçgen sayının karesidir. Olasılıkların kendileri sırasıyla Nichomachus kimliğinin sol ve sağ taraflarıdır, her iki tarafı da $n$ $4'e$ bölerek olasılıkları oluşturmak için normalleştirilir . $P[\max(X,Y,Z)\leq W]=P[X\leq Y\wedge Z\leq W]$

Kanıtlar

Charles Wheatstone ( 1854 ), toplamdaki her bir küpü bir dizi ardışık tek sayıya genişleterek özellikle basit bir türev verir. Kimliğini vererek başlar

n^{3}=\underbrace {\left(n^{2}-n+1\right)+\left(n^{2}-n+1+2\right)+\left(n ^{2}-n+1+4\sağ)+\cdots +\left(n^{2}+n-1\sağ)} _{n{\text{ ardışık tek sayılar}}}.

Bu özdeşlik üçgen sayılarla şu şekilde ilişkilidir :

{\görüntüleme stili T_{n}}

n^{3}=\sum _{k=T_{n-1}+1}^{T_{n}}(2k-1),

ve böylece summands oluşturan hemen sonra önceki tüm değerleri oluşturan kişiler başlamak kadar . Bu özelliği, iyi bilinen başka bir kimlikle birlikte uygulamak:

{\görüntüleme stili n^{3}}

{\görüntüleme stili 1^{3}}

{\görüntüleme stili (n-1)^{3}}

n^{2}=\sum _{k=1}^{n}(2k-1),

aşağıdaki türetmeyi üretir:

{\begin{aligned}\sum _{k=1}^{n}k^{3}&=1+8+27+64+\cdots +n^{3}\\&=\underbrace {1} _{1^{3}}+\underbrace {3+5} _{2^{3}}+\underbrace {7+9+11} _{3^{3}}+\underbrace {13 +15+17+19} _{4^{3}}+\cdots +\underbrace {\left(n^{2}-n+1\right)+\cdots +\left(n^{2}+ n-1\sağ)} _{n^{3}}\\&=\underbrace {\underbrace {\underbrace {\underbrace {1} _{1^{2}}+3} _{2^{2 }}+5} _{3^{2}}+\cdots +\left(n^{2}+n-1\sağ)} _{\left({\frac {n^{2}+n} {2}}\sağ)^{2}}\\&=(1+2+\cdots +n)^{2}\\&={\bigg (}\sum _{k=1}^{n }k{\bigg )}^{2}.\end{hizalı}}

Row (1893) , bir kare çarpım tablosundaki sayıları iki farklı şekilde toplayarak başka bir ispat elde eder . inci satırın toplamı çarpı bir üçgen sayıdır, bundan tüm satırların toplamının bir üçgen sayının karesi olduğu sonucu çıkar. Alternatif olarak, tablo , her biri iki terimden büyük olanın sabit bir değer olduğu ürünlerden oluşan bir iç içe gnomon dizisine ayrıştırılabilir . Her bir gmononun içindeki toplam bir küptür, yani tüm tablonun toplamı bir küp toplamıdır. ${\görüntüleme stili ben}$ ${\görüntüleme stili ben}$

Üçgen bir sayının karesinin bir küp toplamına eşit olduğunun görsel gösterimi.

Daha yakın tarihli matematiksel literatürde, Edmonds (1957) , parçalara göre toplama kullanarak bir ispat sağlar . Stein (1971) , kimliğin geometrik bir kanıtını oluşturmak için bu sayıların dikdörtgen sayma yorumunu kullanır (ayrıca bkz. Benjamin, Quinn & Wurtz 2006 ); bunun tümevarım yoluyla da kolayca (ama bilgi vermeyen bir şekilde) kanıtlanabileceğini gözlemler ve Toeplitz'in (1963) "ilginç bir eski Arapça kanıt" sağladığını belirtir . Kanim (2004) , tamamen görsel bir kanıt sağlar, Benjamin & Orrison (2002) iki ek kanıt sunar ve Nelsen (1993) yedi geometrik kanıt verir.

genellemeler

Nicomachus'un teoremine benzer bir sonuç, tüm güç toplamları için geçerlidir , yani tek güç toplamları (tek güçlerin toplamları) üçgen sayılarda bir polinomdur. Bunlara Faulhaber polinomları denir ve en basit ve en zarif örneği küplerin toplamıdır. Ancak, başka hiçbir durumda bir kuvvet toplamı diğerinin karesi değildir.

Stroeker (1995) , ardışık bir küp dizisinin toplamının bir kare oluşturduğu daha genel koşulları inceler. Garrett & Hummel (2004) ve Warnaar (2004) polinom serilerinin başka bir polinomun karesine eklendiği kare üçgen sayı formülünün polinom analoglarını inceler.

Notlar

Referanslar

Benjamin, Arthur T. ; Orrison, ME (2002), "İki hızlı kombinatoryal kanıt " $\textstyle \sum k^{3}={n+1 \2'yi seçin}^{2}$ (PDF) , College Mathematics Journal , 33 (5): 406–408, doi : 10.2307/1559017 , JSTOR 1559017.
Benjamin, Arthur T. ; Quinn, Jennifer J .; Wurtz, Calyssa (2006), "Dikdörtgenleri sayarak küpleri toplama " (PDF) , College Mathematics Journal , 37 (5): 387–389, doi : 10.2307/27646391 , JSTOR 27646391.
Bressoud, David (2004), Newton ve Leibniz'den Önce Matematik, Bölüm III (PDF) , AP Central.
Edmonds, Sheila M. (1957), "Doğal sayıların kuvvetlerinin toplamı ", The Mathematical Gazette , 41 : 187–188, doi : 10.2307/3609189 , JSTOR 3609189 , MR 0096615
Garrett, Kristina C.; Hummel, Kristen (2004), " $q-$ cubes toplamının kombinatoryal kanıtı " , Electronic Journal of Combinatorics , 11 (1), Research Paper 9, doi : 10.37236/1762 , MR 2034423.
Gulley, Ned (4 Mart 2010), Shure, Loren (ed.), Nicomachus Teoremi , Matlab Central.
Kanim, Katherine (2004), "Kelimesiz İspatlar: Küplerin toplamı—Arşimet'in kareler toplamının bir uzantısı", Mathematics Magazine , 77 (4): 298–299, doi : 10.2307/3219288 , JSTOR 3219288.
Nelsen, Roger B. (1993), Sözsüz Kanıtlar , Cambridge University Press, ISBN 978-0-88385-700-7.
Pengelley, David (2002), "Orijinal kaynaklar aracılığıyla sürekli ve ayrık arasındaki köprü", Study the Masters: The Abel-Fauvel Konferansı (PDF) , National Center for Mathematics Education, Univ. Göteborg, İsveç.
Row, T. Sundara (1893), Kağıt Katlamada Geometrik Alıştırmalar , Madras: Addison, s. 47-48.
Stein, Robert G. (1971), "Bir kombinatoryal kanıt ki ", Mathematics Magazine , 44 (3): 161-162, doi : 10.2307/2688231 , JSTOR 2688231 $\textstyle \sum k^{3}=(\sum k)^{2}$ .
Stroeker, RJ (1995), "Ardışık küplerin toplamının tam kare olması üzerine" , Compositio Mathematica , 97 (1–2): 295–307, MR 1355130.
Toeplitz, Otto (1963), Matematik, Genetik Bir Yaklaşım , University of Chicago Press, ISBN 978-0-226-80667-9.
Warnaar, S. Ole (2004), " Küplerin toplamının $q$ -analogunda" , Electronic Journal of Combinatorics , 11 (1), Not 13, doi : 10.37236/1854 , MR 2114194.
Wheatstone, C. (1854), "Aritmetik ilerlemelerden güçlerin oluşumu üzerine" (PDF) , Proceedings of the Royal Society of London , 7 : 145–151, doi : 10.1098/rspl.1854.0036.

Languages

In other projects