Laplace–Runge–Lenz vektörü - Laplace–Runge–Lenz vector

Bu makale boyunca, vektörler ve büyüklükleri sırasıyla kalın ve italik yazı tipiyle belirtilmiştir. Örneğin, .${\displaystyle \sol|\mathbf {A} \sağ|=A}$

Olarak klasik mekanik , Laplace-Runge Lenz (OML) vektörü a, vektör şekli ve yönünü açıklamak için aşağıda ele alınmıştır yörünge ve bir diğer yaklaşık bir astronomik gövdenin ikili yıldız ya da bir yıldız etrafında dönen bir gezegen. İçin etkileşen iki cisim tarafından Newton yerçekimi , OML vektör, hareket sabit o yörüngede hesaplanır olursa olsun aynı olduğu anlamına gelmektedir; eşdeğer olarak, LRL vektörünün korunduğu söylenir . Daha genel olarak, OML vektörünün iki gövdeler ile etkileşime tüm sorunlar muhafaza edilir merkezi bir kuvvet olarak değişiraralarındaki mesafenin ters karesi ; bu tür problemlere Kepler problemleri denir .

Hidrojen atomu tarafından değerlendirilmiş etkileşen iki yüklü parçacıklar içerir, çünkü bir Kepler sorundur Coulomb yasası bir elektrostatik , bir ters-kare, merkezi kuvvet. LRL vektörü, Schrödinger denkleminin geliştirilmesinden önce, hidrojen atomunun spektrumunun ilk kuantum mekanik türevinde esastı . Ancak bu yaklaşım günümüzde nadiren kullanılmaktadır.

Klasik ve kuantum mekaniğinde, korunan nicelikler genellikle sistemin bir simetrisine karşılık gelir . LRL vektörünün korunumu alışılmadık bir simetriye karşılık gelir; Kepler problemi, dört boyutlu (hiper) bir kürenin yüzeyinde serbestçe hareket eden bir parçacığa matematiksel olarak eşdeğerdir , böylece tüm problem dört boyutlu uzayın belirli dönüşleri altında simetriktir. Bu daha yüksek simetri, Kepler probleminin iki özelliğinden kaynaklanır: hız vektörü her zaman mükemmel bir daire içinde hareket eder ve belirli bir toplam enerji için , bu tür tüm hız daireleri aynı iki noktada kesişir.

Laplace–Runge–Lenz vektörü, Pierre-Simon de Laplace , Carl Runge ve Wilhelm Lenz'in adını almıştır . Ayrıca olarak bilinen Laplace vektörü , Runge-Lenz vektörü ve Lenz vektörü . İronik olarak, bu bilim adamlarının hiçbiri onu keşfetmedi. LRL vektörü birkaç kez yeniden keşfedildi ve yeniden formüle edildi; örneğin, boyutsuz eşdeğerdir dışmerkezlik vektörünün bir gök mekaniği . LRL vektörünün özel göreliliğin , elektromanyetik alanların ve hatta farklı tipteki merkezi kuvvetlerin etkilerini içeren çeşitli genellemeleri tanımlanmıştır .

Bağlam

Herhangi biri uyarınca bir tek parçacık hareketli tutucu toplam enerji: merkezi bir kuvvet hareketin en az dört sabitleri olan E ve üç Kartezyen bileşenleri arasında açısal momentum vektörü L kuvvet merkezine göre. Parçacığın yörüngesi, parçacığın başlangıç momentumu p (veya eşdeğer olarak hızı v ) ve parçacık ile kuvvet merkezi arasındaki r vektörü tarafından tanımlanan düzlemle sınırlıdır (bkz. Şekil 1). Bu hareket düzlemi sabit açısal momentum vektörüne diktir L = r × p ; bu, vektör nokta çarpım denklemi r ⋅ L = 0 ile matematiksel olarak ifade edilebilir . Aşağıdaki matematiksel tanımı verildiğinde , Laplace–Runge–Lenz vektörü (LRL vektörü) A , tüm merkezi kuvvetler için ( A ⋅ L = 0 ) sabit açısal momentum vektörü L'ye her zaman diktir . Bu nedenle A daima hareket düzleminde yer alır. Aşağıda gösterildiği gibi , A kuvvet merkezinden hareketin periapsis noktasına, en yakın yaklaşma noktasına işaret eder ve uzunluğu yörüngenin eksantrikliği ile orantılıdır.

LRL vektörü A , uzunluk ve yön bakımından sabittir, ancak yalnızca ters kare merkezi kuvvet için. Diğer merkezi kuvvetler için A vektörü sabit değildir, hem uzunluk hem de yön olarak değişir. Merkezi kuvvet yaklaşık olarak bir ters kare yasasıysa, A vektörünün uzunluğu yaklaşık olarak sabittir, ancak yönünü yavaşça döndürür. Bir genelleştirilmiş korunmuş OML vektörü tanımlanabilir tüm merkezi kuvvetleri için, ancak bu genel vektör genellikle pozisyonda karmaşık bir fonksiyondur, ve kapalı formda eksprese . ${\görüntüleme stili {\matematiksel {A}}}$

LRL vektörü, aşağıdaki özellik bakımından diğer korunan niceliklerden farklıdır. Tipik olarak korunmuş miktarlarda ise, tekabül eden bir orada koordinat siklik üç boyutlu olarak Lagrange sistemi vardır etmez olmayan OML vektörü için koordinat örneğin a mevcuttur. Bu nedenle, LRL vektörünün korunumu doğrudan, örneğin aşağıda açıklandığı gibi Poisson parantezleri yöntemiyle türetilmelidir . Bu tür korunan niceliklere, örneğin açısal momentumunki gibi olağan "geometrik" korunum yasalarının aksine "dinamik" denir.

Yeniden keşif tarihi

LRL vektörü A , Kepler probleminin bir hareket sabitidir ve gezegenlerin ve ikili yıldızların hareketi gibi astronomik yörüngeleri tanımlamada faydalıdır. Yine de, muhtemelen momentum ve açısal momentumdan daha az sezgisel olduğu için fizikçiler arasında hiçbir zaman iyi bilinmedi. Sonuç olarak, son üç yüzyılda bağımsız olarak birkaç kez yeniden keşfedildi.

Jakob Hermann , A'nın ters kare merkez kuvvetinin özel bir durumu için korunduğunu gösteren ilk kişiydi ve yörünge elipsinin eksantrikliği ile bağlantısını çözdü . Hermann'ın çalışması, 1710'da Johann Bernoulli tarafından modern biçimine genelleştirildi . Yüzyılın sonunda, Pierre-Simon de Laplace, A'nın korunumunu geometrik yerine analitik olarak türeterek yeniden keşfetti . On dokuzuncu yüzyılın ortalarında, William Rowan Hamilton , aşağıda tanımlanan eşdeğer eksantriklik vektörünü türetmiş ve bunu momentum vektörü p'nin bir ters kare merkezi kuvvet altında hareket için bir daire üzerinde hareket ettiğini göstermek için kullanmıştır (Şekil 3).

Yirminci yüzyılın başında, Josiah Willard Gibbs aynı vektörü vektör analizi ile elde etti . Gibbs'in türetilmesi, Carl Runge tarafından vektörler üzerine popüler bir Alman ders kitabında, Wilhelm Lenz tarafından hidrojen atomunun (eski) kuantum mekaniksel işlemine ilişkin makalesinde atıfta bulunulan bir örnek olarak kullanıldı . 1926'da Wolfgang Pauli , kuantum mekaniğinin matris mekaniği formülasyonunu kullanarak hidrojen atomunun enerji seviyelerini türetmek için LRL vektörünü kullandı ve daha sonra esas olarak Runge-Lenz vektörü olarak bilinmeye başladı .

matematiksel tanım

Tek bir parçacık üzerine etkiyen ters kare merkezi kuvvet denklem ile tanımlanır.

${\displaystyle \mathbf {F} (r)=-{\frac {k}{r^{2}}}\mathbf {\hat {r}} ;}$

Karşılık gelen potansiyel enerji ile verilir . Sabit parametre k , merkezi kuvvetin gücünü tanımlar; Bu eşittir G ⋅ M ⋅ m yerçekimi ve için - k _e ⋅ Q ⋅ q elektrostatik kuvvetler için. Kuvvet k > 0 ise çekici , k < 0 ise iticidir . ${\displaystyle V(r)=-{\frac {k}{r}}}$

Şekil 1: Ters-kare merkezi kuvvet altında hareket eden bağlı bir nokta parçacığının eliptik yörüngesinde dört noktada (1, 2, 3 ve 4 olarak etiketlenmiş) LRL vektörü A (kırmızı ile gösterilmiştir). Çekim merkezi, konum vektörlerinin (aynı şekilde siyah) çıktığı küçük siyah bir daire olarak gösterilir. Açısal momentum vektörü L yörüngeye diktir. Eş düzlemli vektörler p × L ve ( mk / r ) r sırasıyla mavi ve yeşil olarak gösterilmiştir; Bu değişkenler tanımlandığı aşağıdaki . A vektörü yön ve büyüklük olarak sabittir.

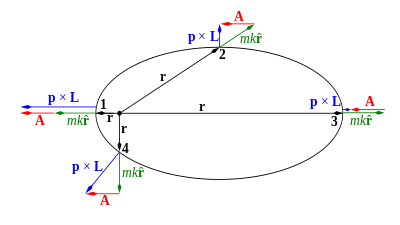
LRL vektörü A , matematiksel olarak formülle tanımlanır.

nerede

• m , merkezi kuvvet altında hareket eden nokta parçacığın kütlesidir ,
• p momentum vektörüdür,
• L = r × p açısal momentum vektörüdür,
• r parçacığın konum vektörüdür (Şekil 1),
• ${\displaystyle \mathbf {\hat {r}} }$karşılık gelen birim vektör , yani , ve${\displaystyle \mathbf {\hat {r}} ={\frac {\mathbf {r} }{r}}}$
• r büyüklüğüdür r , kuvvet merkezi kütle mesafe.

SI birimleri OML vektörünün jul kilogram-metre (J⋅kg⋅m) vardır. Bunun nedeni, p ve L birimlerinin sırasıyla kg⋅m/s ve J⋅s olmasıdır. Bu, m (kg) ve k (N⋅m ² ) birimleriyle uyumludur .

LRL vektörü A'nın bu tanımı, sabit bir kuvvetin etkisi altında hareket eden m kütleli tek nokta parçacıkla ilgilidir . Bununla birlikte, aynı tanım, iki cismin indirgenmiş kütlesi olarak m ve iki cisim arasındaki vektör olarak r alınarak, Kepler problemi gibi iki cisim problemlerine genişletilebilir .

Varsayılan kuvvet korunumlu olduğundan, toplam enerji E bir hareket sabitidir,

${\displaystyle E={\frac {p^{2}}{2m}}-{\frac {k}{r}}={\frac {1}{2}}mv^{2}-{\frac {k}{r}}.}$

Varsayılan kuvvet aynı zamanda merkezi bir kuvvettir. Dolayısıyla açısal momentum vektörü L de korunur ve parçacığın içinde hareket ettiği düzlemi tanımlar. Vektör OML A açısal momentum vektörü dik olan L çünkü her iki p x L ve R dik olan L . Bu izler bir hareket düzleminde uzanır.

Aynı hareket sabiti için alternatif formülasyonlar, tipik olarak vektörü kütle m , kuvvet parametresi k veya açısal momentum L gibi sabitlerle ölçeklendirerek tanımlanabilir . En sık görülen bölmektir A ile mk eksantriklik vektörü, verimleri, boyutsuz modülü konik eksantriklik eşit yarı-büyük eksen boyunca vektör:

${\displaystyle \mathbf {e} ={\frac {\mathbf {A} }{mk}}={\frac {1}{mk}}(\mathbf {p} \times \mathbf {L} )-\ matematik {\hat {r}} .}$

Eşdeğer bir formülasyon, bu eksantriklik vektörünü ana yarım eksen a ile çarparak elde edilen vektöre uzunluk birimlerini verir. Yine bir başka formülasyon, bölme A ile ters uzunluk birimleri, bir miktar ile eşdeğer bir korunmuş miktarı, sonuçta bu Kepler sorunun çözümünde görünür ${\ Displaystyle L^{2}}$

${\displaystyle u\equiv {\frac {1}{r}}={\frac {km}{L^{2}}}+{\frac {A}{L^{2}}}\cos \theta }$

A ve konum vektörü r arasındaki açı nerede . Ayrıca, alternatif karışımlar verilmiştir aşağıda . ${\görüntüleme stili\teta }$

Kepler yörüngelerinin türetilmesi

Şekil 2: Yörüngenin bir noktasında A ve r arasındaki θ açısını tanımlayan Şekil 1'in basitleştirilmiş versiyonu .

Şekil ve yönlendirme aşağıdaki gibi yörüngelerin OML vektöründen belirlenebilir. A'nın nokta çarpımını konum vektörü r ile almak denklemi verir

${\displaystyle \mathbf {A} \cdot \mathbf {r} =A\cdot r\cdot \cos \theta =\mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L}} sağ)-mkr,}$

burada θ , r ve A arasındaki açıdır (Şekil 2). NN karma çarpımlar verimi

${\displaystyle \mathbf {r} \cdot \left(\mathbf {p} \times \mathbf {L} \sağ)=\left(\mathbf {r} \times \mathbf {p} \sağ)\cdot \ mathbf {L} =\mathbf {L} \cdot \mathbf {L} =L^{2}}$

Yeniden düzenleme Kepler denkleminin çözümünü verir

Bu, dışmerkezlik e'nin konik bir bölümü için formüle karşılık gelir.

${\displaystyle {\frac {1}{r}}=C\cdot \left(1+e\cdot \cos \theta \sağ)}$

burada eksantriklik ve C bir sabittir. ${\displaystyle e={\frac {A}{\sol|mk\sağ|}}\geq 0}$

A'nın nokta ürününü kendisiyle birlikte almak, toplam E enerjisini içeren bir denklem verir ,

${\displaystyle A^{2}=m^{2}k^{2}+2mEL^{2},}$

eksantriklik açısından yeniden yazılabilir,

${\displaystyle e^{2}=1+{\frac {2L^{2}}{mk^{2}}}E.}$

Bu nedenle, eğer E enerjisi negatifse (bağlı yörüngeler), dışmerkezlik birden küçüktür ve yörünge bir elipstir. Tersine, eğer enerji pozitifse ("dağılmış yörüngeler" olarak da adlandırılan bağlı olmayan yörüngeler), eksantriklik birden büyüktür ve yörünge bir hiperboldür . Son olarak, eğer enerji tam olarak sıfırsa, eksantriklik bir ve yörünge bir paraboldür . Her durumda, A yönü , konik bölümün simetri ekseni boyunca uzanır ve kuvvet merkezinden en yakın yaklaşma noktası olan periapsis'e doğru işaret eder.

Dairesel momentum hodografları

Şekil 3: Momentum vektörü p (mavi ile gösterilmiştir), parçacık bir elips üzerinde hareket ederken bir daire üzerinde hareket eder. Dört etiketli nokta, Şekil 1'dekilere karşılık gelir. Daire, A / L konumunda (macenta ile gösterilmiştir), mk / L yarıçapıyla (yeşille gösterilmiştir ) y ekseninde ortalanmıştır . η açısı , eliptik yörüngenin (cos  η =  e ) dışmerkezliğini e belirler . Tarafından yazılmıştır açı teoremi için çevrelerinde , η çember üzerinde herhangi bir noktaya ile iki kesişme noktası arasındaki açı da p _x ekseni, s _x = ± p ₀ , sadece bağlıdır, E , ama L .

LRL vektörü A ve açısal momentum vektörü L' nin korunumu, momentum vektörü p'nin bir daire üzerinde ters kare merkezi kuvvet altında hareket ettiğini göstermede faydalıdır .

nokta çarpımını alarak

${\displaystyle mk{\hat {\mathbf {r} }}=\mathbf {p} \times \mathbf {L} -\mathbf {A} }$

kendisi ile verim

${\displaystyle (mk)^{2}=A^{2}+p^{2}L^{2}+2\mathbf {L} \cdot (\mathbf {p} \times \mathbf {A} ) .}$

Ayrıca z ekseni boyunca L' yi ve x ekseni olarak ana yarı ekseni seçmek , p için yer denklemini verir ,

Başka bir deyişle, momentum vektörü p , (0, A / L ) merkezli mk/L = L / ℓ yarıçaplı bir daireyle sınırlıdır . Eksantriklik e , Şekil 3'te gösterilen η açısının kosinüsüne karşılık gelir .

Dairesel yörüngelerin dejenere sınırında ve dolayısıyla A kaybolan daire, orijinde (0,0) merkezlenir. Kısaca, değişkeni tanıtmak da yararlıdır . ${\displaystyle p_{0}={\sqrt {2m|E|}}}$

Bu dairesel hodograf , Kepler probleminin simetrisini göstermede faydalıdır.

Hareket sabitleri ve süper bütünleşebilirlik

Yedi skaler büyüklük E , A ve L (vektörlerdir, son ikisi her biri üç korunmuş niceliğe katkıda bulunur) iki denklemle ilişkilidir, A ⋅ L = 0 ve A ² = m ² k ² + 2 mEL ² , beş bağımsız sabit verir hareketin . (Büyüklüğü yana A , bu nedenle eksantriklik e yörüngesinin, toplam açısal momentum belirlenebilir L ve enerji E , sadece yön arasında A , bağımsız bir şekilde muhafaza edilir, çünkü bundan başka, bir dik olmalıdır L , bu katkı sadece bir ek korunan miktar.)

Bu, başlangıç ​​zamanı bir hareket sabiti tarafından belirlenmediğinden, parçacığın yörüngesini belirleyen altı başlangıç ​​koşuluyla (parçacığın başlangıç ​​konumu ve hız vektörleri, her biri üç bileşenli) tutarlıdır. 6 boyutlu faz uzayında elde edilen 1 boyutlu yörünge böylece tamamen belirlenir.

d serbestlik derecesine sahip bir mekanik sistem , 2 d başlangıç ​​koşulu olduğundan ve başlangıç ​​zamanı bir hareket sabiti ile belirlenemediğinden , en fazla 2 d − 1 hareket sabitine sahip olabilir. d' den fazla hareket sabiti olan bir sisteme süper bütünleşebilir , 2 d - 1 sabiti olan bir sisteme maksimum üst bütünleşebilir denir . Çözeltisi yana Hamilton-Jacobi denklemi bir de koordinat sistemi sadece verebilmesidir d hareket sabitleri, superintegrable sistemleri bir koordinat sistemi daha parçalanabilir olması gerekir. Kepler problemi, üç serbestlik derecesine ( d = 3 ) ve beş bağımsız hareket sabitine sahip olduğu için maksimum düzeyde üst bütünleştirilebilir ; Hamilton'daki-Jacobi denklemi hem de ayrılabilir olan küresel koordinatlar ve parabolik koordinatları anlatıldığı gibi, aşağıdaki .

En üst düzeyde bütünleştirilebilir sistemler, faz uzayında kapalı, tek boyutlu yörüngeleri takip eder , çünkü yörünge, hareket sabitlerinin faz-uzay eşyüzeylerinin kesişimidir . Sonuç olarak, yörüngeler, bu özel problemde beş olmak üzere tüm bu bağımsız eşyüzeylerin tüm gradyanlarına diktir ve dolayısıyla tüm bu gradyanların genelleştirilmiş çapraz ürünleri tarafından belirlenir. Sonuç olarak, tüm üst bütünleşebilir sistemler, otomatik olarak Nambu mekaniği tarafından , alternatif olarak ve eşdeğer olarak Hamilton mekaniği ile tanımlanabilir .

Aşağıda gösterildiği gibi , en üst düzeyde bütünleştirilebilir sistemler , komütasyon ilişkileri kullanılarak nicelenebilir . Bununla birlikte, eşdeğer olarak, bu klasik Kepler problemi gibi, kuantum hidrojen atomuna Nambu çerçevesinde de nicelenirler.

Bozulmuş potansiyeller altında evrim

Şekil 5: Eksantriklik e  = 0,667 olan kademeli olarak ilerleyen eliptik yörünge . Çekici merkezi kuvvet bir ters kare yasasından biraz saparsa, Kepler probleminde böyle bir presesyon ortaya çıkar. Oran Presesyonun metninde formüller kullanılarak hesaplanabilir.

Laplace–Runge–Lenz vektörü A yalnızca mükemmel bir ters kare merkezi kuvvet için korunur. Bununla birlikte, gezegensel hareket gibi çoğu pratik problemde, iki cisim arasındaki etkileşim potansiyel enerjisi tam olarak bir ters kare kanunu değildir, ancak bir potansiyel enerji h ( r ) tarafından tanımlanan pertürbasyon olarak adlandırılan ek bir merkezi kuvveti içerebilir . Bu gibi durumlarda, LRL vektörü, yörüngenin yavaş apsisli bir devinmesine karşılık gelen yörünge düzleminde yavaşça döner .

Varsayım olarak, bozucu potansiyel h ( r ) korunumlu bir merkezi kuvvettir, bu da toplam enerji E ve açısal momentum vektörü L' nin korunduğunu ima eder . Dik olan bir düzlemde Böylece, hareket halen yalan L ve büyüklüğü A denklemi ile ilgili, muhafaza edilir A ² = m ² k ² + 2 mel ² . Pertürbasyon potansiyeli h ( r ) herhangi bir fonksiyon olabilir, ancak iki cisim arasındaki ana ters kare kuvvetten önemli ölçüde daha zayıf olmalıdır.

Oranı hangi OML vektör döndüğü bozucu potansiyel hakkında bilgi sağlar saat ( r ) . Kanonik pertürbasyon teorisi ve eylem açısı koordinatlarını kullanarak, A'nın şu hızda döndüğünü göstermek kolaydır:

${\displaystyle {\begin{aligned}{\frac {\partial }{\partial L}}\langle h(r)\rangle &=\displaystyle {\frac {\partial }{\partial L}}\left\ {{\frac {1}{T}}\int _{0}^{T}h(r)\,dt\right\}\\[1em]&=\displaystyle {\frac {\partial }{\ kısmi L}}\left\{{\frac {m}{L^{2}}}\int _{0}^{2\pi }r^{2}h(r)\,d\theta \right \},\end{hizalanmış}}}$

burada T yörünge periyodudur ve zaman integralini açısal integrale dönüştürmek için L dt = m r ² dθ kimliği kullanılmıştır (Şekil 5). Köşeli parantez içindeki ifade, ⟨ h ( r )⟩ , rahatsız edici potansiyeli temsil eder, ancak bir tam periyot üzerinden ortalaması alınır ; yani, vücudun yörüngesi etrafındaki bir tam geçişinin ortalaması alınır. Matematiksel olarak, bu zaman ortalaması kaşlı ayraçlarda aşağıdaki miktara karşılık gelir. Bu ortalama alma, dönme hızındaki dalgalanmaları bastırmaya yardımcı olur.

Bu yaklaşım, Einstein'ın normal Newton kütleçekimi potansiyeline küçük bir etkili ters kübik bozulma ekleyen genel görelilik teorisini doğrulamaya yardımcı olmak için kullanıldı.

${\displaystyle h(r)={\frac {kL^{2}}{m^{2}c^{2}}}\left({\frac {1}{r^{3}}}\sağ ).}$

Bu fonksiyonu integrale eklemek ve denklemi kullanmak

${\displaystyle {\frac {1}{r}}={\frac {mk}{L^{2}}}\left(1+{\frac {A}{mk}}\cos \theta \sağ) }$

r'yi θ cinsinden ifade etmek için , bu Newtonyen olmayan pertürbasyonun neden olduğu periapsisin presesyon oranı şu şekilde hesaplanır:

${\displaystyle {\frac {6\pi k^{2}}{TL^{2}c^{2}}},}$

Merkür ve ikili pulsarların gözlemlenen anormal devinimiyle yakından eşleşen . Deneyle olan bu anlaşma, genel görelilik için güçlü bir kanıttır.

zehir parantez

Ölçeklendirilmemiş fonksiyonlar

Problemin cebirsel yapısı, daha sonraki bölümlerde açıklandığı gibi, SO(4)/ℤ ₂ ~ SO(3) × SO(3)'tür. Üç bileşen L _i açısal momentum vektörü L Poisson parantez sahip

${\displaystyle \{L_{i},L_{j}\}=\sum _{s=1}^{3}\varepsilon _{ijs}L_{s},}$

burada i =1,2,3 ve ϵ _ijs tamamen antisimetrik tensördür , yani Levi-Civita sembolüdür ; s toplama indeksi , yukarıda tanımlanan kuvvet parametresi k ile karışıklığı önlemek için burada kullanılır . LRL vektörü A bir vektör gibi dönüştüğü için, A ve L arasında aşağıdaki Poisson parantez bağıntılarına sahibiz :

${\displaystyle \{A_{i},L_{j}\}=\sum _{s=1}^{3}\varepsilon _{ijs}A_{s}.}$

Son olarak, A'nın farklı bileşenleri arasındaki Poisson parantez ilişkileri aşağıdaki gibidir:

${\displaystyle \{A_{i},A_{j}\}=-2mH\sum _{s=1}^{3}\varepsilon _{ijs}L_{s},}$

Hamiltoniyen nerede . A'nın bileşenlerinin ve L' nin bileşenlerinin açıklığının , bu son ilişkinin sağ tarafındaki faktörü nedeniyle Poisson parantezleri altında kapalı olmadığına dikkat edin . ${\görüntüleme stili H}$${\görüntüleme stili H}$

Her iki yana Nihayet, L ve A hareket sabitlerdir, elimizdeki

${\displaystyle \{A_{i},H\}=\{L_{i},H\}=0.}$

Poisson parantezleri kuantum mekanik uzatılacak komütasyon ilişkileri içinde sonraki bölümde ve Lie parantez bir de aşağıdaki bölümde .

Ölçekli fonksiyonlar

Belirtildiği gibi , aşağıda , bir ölçekli Laplace-Runge Lenz vektörü D bölünmesi ile açısal momentum ile aynı birimlerle tanımlanabilir A ile . Yana D yine bir vektör gibi dönüştürür, Poisson parantez D açısal momentum vektörü ile L sonra benzer biçimde yazılabilir ${\displaystyle p_{0}={\sqrt {2m|H|}}}$

${\displaystyle \{D_{i},L_{j}\}=\sum _{s=1}^{3}\varepsilon _{ijs}D_{s}.}$

Poisson parantez D ile kendi bağımlı işareti arasında H enerji olup, diğer bir deyişle, negatif (kapalı üreten, eliptik yörünge ters-kare, merkezi kuvvet altında) ya da pozitif merkezi (bir alt, açık, hiperbolik yörüngeleri üreten ters-kare Kuvvet). İçin negatif enerjileri-bir deyişle, bağlanan sistemlerinin-Poisson braketlerdir

${\displaystyle \{D_{i},D_{j}\}=\sum _{s=1}^{3}\varepsilon _{ijs}L_{s}.}$

Şimdi D' nin seçilen ölçeklemesi için motivasyonu takdir edebiliriz : Bu ölçekleme ile Hamiltonyen artık önceki ilişkinin sağ tarafında görünmez. Böylece, L' nin üç bileşeninin ve D' nin üç bileşeninin açıklığı , Poisson parantezinin altında altı boyutlu bir Lie cebiri oluşturur. Bu Lie cebri, 4 boyutlu döndürme grubu SO(4)'ün Lie cebri olan so(4) ile eşbiçimlidir.

Buna karşılık, pozitif enerji için Poisson parantezleri zıt işarete sahiptir,

${\displaystyle \{D_{i},D_{j}\}=-\sum _{s=1}^{3}\varepsilon _{ijs}L_{s}.}$

Bu durumda, Lie cebiri so(3,1) ile eşbiçimlidir.

Pozitif ve negatif enerjiler arasındaki ayrım, istenen ölçeklemenin -ölçekli LRL vektörünün bileşenleri arasındaki Poisson parantez ilişkilerinin sağ tarafından Hamiltoniyeni ortadan kaldıran- Hamiltoniyenin karekökünü içermesinden kaynaklanır . Gerçek değerli fonksiyonlar elde etmek için, pozitif değerler (nerede ) ve negatif değerler (nerede ) arasında ayrım yapan Hamiltonian'ın mutlak değerini almalıyız . ${\görüntüleme stili |H|=H}$${\görüntüleme stili |H|=-H}$

Casimir değişmezleri ve enerji seviyeleri

Casimir değişmezler negatif enerjileri içindir

${\displaystyle C_{1}=\mathbf {D} \cdot \mathbf {D} +\mathbf {L} \cdot \mathbf {L} ={\frac {mk^{2}}{2|E|} },}$

${\displaystyle C_{2}=\mathbf {D} \cdot \mathbf {L} =0,}$

ve D ve L' nin tüm bileşenleriyle birlikte kaybolan Poisson braketlerine sahip ,

${\displaystyle \{C_{1},L_{i}\}=\{C_{1},D_{i}\}=\{C_{2},L_{i}\}=\{C_{2 },D_{i}\}=0.}$

İki vektör her zaman dik olduğundan, C ₂ önemsizdir.

Bununla birlikte, diğer değişmez, Cı ₁ , önemsiz olmayan ve sadece bağlıdır m , k ve E . Kanonik kuantizasyon üzerine, bu değişmez, hidrojen benzeri atomların enerji seviyelerinin , Schrödinger denkleminin geleneksel çözümü yerine sadece kuantum mekanik kanonik komütasyon ilişkileri kullanılarak türetilmesine izin verir . Bu türetme bir sonraki bölümde ayrıntılı olarak tartışılmaktadır.

Hidrojen atomunun kuantum mekaniği

Şekil 6: Açısal momentum ve Laplace–Runge–Lenz vektör operatörlerinin komütasyon ilişkilerinden tahmin edildiği gibi hidrojen atomunun enerji seviyeleri; bu enerji seviyeleri deneysel olarak doğrulanmıştır.

Poisson parantezleri çoğu klasik sistemin nicelenmesi için basit bir kılavuz sağlar: iki kuantum mekanik operatörünün komütasyon ilişkisi , karşılık gelen klasik değişkenlerin Poisson paranteziyle iħ ile çarpılarak belirlenir .

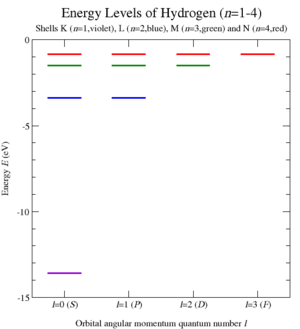
Bu niceleme yapılması ve öz hesaplayarak Cı ₁ Kepler sorunu için Casimir'in operatör Wolfgang Pauli elde etmek mümkün enerji düzeyleri , bu nedenle, kendi atomik emisyon spektrumunu hidrojen benzeri atomlu (Şekil 6) ve. Bu zarif 1926 türevi, Schrödinger denkleminin geliştirilmesinden önce elde edildi .

LRL vektörü A için kuantum mekanik operatörünün inceliklerinden biri, momentum ve açısal momentum operatörlerinin değişmemesidir; bu nedenle, p ve L' nin kuantum operatörü çapraz çarpımı dikkatli bir şekilde tanımlanmalıdır. Tipik olarak, Kartezyen bileşenleri A _s için operatörler simetrik (Hermitian) bir ürün kullanılarak tanımlanır,

${\displaystyle A_{s}=-mk{\hat {r}}_{s}+{\frac {1}{2}}\sum _{i=1}^{3}\sum _{j= 1}^{3}\varepsilon _{sij}(p_{i}\ell _{j}+\ell _{j}p_{i}),}$

Bu yapıldıktan sonra, kuantum LRL operatörlerinin, önceki bölümdeki Poisson parantez ilişkilerine tam olarak benzer komütasyon ilişkilerini sağladığı gösterilebilir - sadece Poisson parantezini komütatör ile değiştirerek. ${\displaystyle 1/(i\hbar )}$

Bu operatörlerden L için ek merdiven operatörleri tanımlanabilir,

${\displaystyle J_{0}=A_{3},}$

${\displaystyle J_{\pm 1}=\mp {\frac {1}{\sqrt {2}}}\left(A_{1}\pm iA_{2}\right).}$

Bu diğer bağlantı farklı bir özdurumları L ² , çok farklı eğirme multiplet, kendi aralarında.

Normalleştirilmiş bir birinci Casimir değişmez operatörü, yukarıdakilerin kuantum analoğu da benzer şekilde tanımlanabilir,

${\displaystyle C_{1}=-{\frac {mk^{2}}{2\hbar ^{2}}}H^{-1}-I,}$

burada H ^-1 , Hamiltonyen enerji operatörünün tersidir ve I , özdeşlik operatörüdür .

Bu merdiven operatörlerini özdurumlara uygulama | Toplam açısal momentum, azimut açısal momentum ve enerji operatörlerinin ℓ mn〉'si, birinci Casimir operatörünün özdeğerleri, C ₁ , nicelenmiş olarak görülüyor, n ² − 1 . Önemli bir şekilde, ufuk kuvvetiyle C ₂ , bu ℓ ve bağımsız m , kuantum sayıları verme seviyesi dejenere enerji .

Bu nedenle, enerji seviyeleri ile verilir

${\displaystyle E_{n}=-{\frac {mk^{2}}{2\hbar ^{2}n^{2}}},}$

bu , hidrojen benzeri atomlar için Rydberg formülüyle örtüşür (Şekil 6). Ek simetri işlemi bir belirli bir enerji (ve, kendi aralarında farklı ℓ çoklular bağladıktan Cı ₁ dikte) n- ² her seviyede durumları. Aslında, bu açısal momentum grubu genişlemiş , SO (3) için SO (4) / ℤ ₂ ~ SO (3) x, SO (3).

Koruma ve simetri

LRL vektörünün korunumu, sistemin ince bir simetrisine karşılık gelir. In klasik mekanik , simetrileri sistemin enerjisini değiştirmeden başka üzerine bir yörüngeye map sürekli işlemlerinden; kuantum mekaniğinde simetriler , aynı enerjinin elektronik yörüngelerini "karıştıran" sürekli işlemlerdir , yani dejenere enerji seviyeleri. Korunmuş bir miktar genellikle bu tür simetrilerle ilişkilendirilir. Örneğin, her merkezi kuvvet dönme grubu SO(3) altında simetriktir , bu da L açısal momentumunun korunmasına yol açar . Klasik olarak, sistemin genel dönüşü bir yörüngenin enerjisini etkilemez; kuantum mekaniksel olarak, rotasyonlar , enerjiyi değiştirmeden aynı kuantum sayısı l' nin küresel harmoniklerini karıştırır .

Şekil 7: Belirli bir enerji E için dairesel momentum hodografları ailesi . Tüm çevreler aynı iki nokta geçmesine ilgili p _X (Şekil 3) ekseni. Bu hodograf ailesi, Apollon çemberlerinin bir ailesine ve bipolar koordinatların σ eşyüzeylerine karşılık gelir .${\displaystyle \pm p_{0}=\pm {\sqrt {2m|E|}}}$

Ters kare merkezi kuvvetin simetrisi daha yüksek ve daha incedir. Kepler probleminin kendine özgü simetrisi, hem açısal momentum vektörü L'nin hem de LRL vektörü A'nın ( yukarıda tanımlandığı gibi ) korunmasıyla sonuçlanır ve kuantum mekaniksel olarak hidrojenin enerji seviyelerinin açısal momentum kuantum sayılarına l bağlı olmamasını sağlar. ve m . Ancak simetri daha incedir, çünkü simetri işlemi daha yüksek boyutlu bir uzayda gerçekleşmelidir ; bu tür simetrilere genellikle "gizli simetriler" denir.

Klasik olarak, Kepler probleminin daha yüksek simetrisi, enerjiyi koruyan ancak açısal momentumu korumayan yörüngelerin sürekli değişimlerine izin verir; başka bir şekilde ifade edilirse, aynı enerjiye sahip ancak farklı açısal momentuma (eksantriklik) sahip yörüngeler sürekli olarak birbirine dönüştürülebilir. Kuantum mekanik olarak, bu , s ( l = 0 ) ve p ( l = 1 ) atomik orbitalleri gibi l ve m kuantum sayılarında farklılık gösteren karıştırma orbitallerine karşılık gelir . Bu tür bir karıştırma, sıradan üç boyutlu ötelemeler veya döndürmeler ile yapılamaz, ancak daha yüksek bir boyuttaki bir döndürmeye eşdeğerdir.

İçin negatif , yani bağlı sistemler için - - enerjileri yüksek simetri grubu dört-boyutlu vektör uzunluğu korumaktadır, (4) SO

${\displaystyle |\mathbf {e} |^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}+e_{4}^{2} .}$

1935'te Vladimir Fock , kuantum mekaniksel bağlı Kepler sorununun, dört boyutlu uzayda üç boyutlu bir birim küreyle sınırlandırılmış serbest parçacık sorununa eşdeğer olduğunu gösterdi . Spesifik olarak Fock , Kepler problemi için momentum uzayındaki Schrödinger dalga fonksiyonunun , küresel harmoniklerin küre üzerindeki stereografik izdüşümü olduğunu gösterdi. Kürenin dönüşü ve yeniden izdüşüm, enerjiyi değiştirmeden eliptik yörüngelerin sürekli bir haritalanmasıyla sonuçlanır, bazen Fock simetrisi olarak bilinen bir SO(4) simetrisi ; kuantum mekaniksel olarak, bu aynı enerji kuantum sayısı n'nin tüm orbitallerinin bir karışımına karşılık gelir . Valentine Bargmann daha sonra açısal momentum vektörü L için Poisson parantezlerinin ve ölçeklenmiş LRL vektörü A'nın SO(4) için Lie cebirini oluşturduğunu kaydetti. Basitçe söylemek gerekirse, altı büyüklük A ve L , o uzaydaki altı olası basit dönüşle ilişkili dört boyutta korunan altı açısal momentuma karşılık gelir (dört eksenden iki eksen seçmenin altı yolu vardır). Bu sonuç, evrenimizin üç boyutlu bir küre olduğu anlamına gelmez ; sadece bu belirli fizik probleminin (ters kare merkez kuvvetleri için iki cisim problemi) üç boyutlu bir küre üzerindeki serbest bir parçacığa matematiksel olarak eşdeğer olduğu anlamına gelir .

İçin pozitif enerjileri - yani, ilişkisiz için, sistemler "dağılmış" - yüksek simetri grubu olduğu , SO (3,1) korur, Minkowsky uzunluğu arasında 4-vektörleri

${\displaystyle ds^{2}=e_{1}^{2}+e_{2}^{2}+e_{3}^{2}-e_{4}^{2}.}$

Hem negatif hem de pozitif enerji vakaları Fock ve Bargmann tarafından değerlendirildi ve Bander ve Itzykson tarafından ansiklopedik olarak gözden geçirildi.

Merkezi kuvvet sistemlerinin ve özellikle Kepler probleminin yörüngeleri de yansıma altında simetriktir . Bu nedenle, yukarıda bahsedilen SO(3), SO(4) ve SO(3,1) grupları yörüngelerinin tam simetri grupları değildir; tam gruplar sırasıyla O(3) , O(4) ve O(3,1) 'dir . Bununla birlikte, açısal momentumun ve LRL vektörlerinin korunumunu göstermek için sadece bağlantılı alt gruplar , SO(3), SO(4) ve SO(3,1) gereklidir; yansıma simetrisi, grubun Lie cebirinden türetilebilen koruma için ilgisizdir.

Dört boyutta dönme simetrisi

Şekil 8: Şekil 7'deki momentum hodografları , üç boyutlu η birim küresi üzerindeki büyük dairelerin stereografik izdüşümlerine karşılık gelir . Tüm büyük daireler , sayfaya dik olan η _x ekseniyle kesişir ; projeksiyon kuzey kutbuna (ila ağırlık birim vektörü) η _X - η _y kesik siyah çizgilerle kırmızı hodograf için, burada gösterildiği gibi, düzlem. α enlemindeki büyük daire, e = sin α eksantrikliğine karşılık gelir . Burada gösterilen büyük dairelerin renkleri, Şekil 7'deki eşleşen hodograflarına karşılık gelir.

Kepler problemi ile dört boyutlu dönme simetrisi SO(4) arasındaki bağlantı kolaylıkla görselleştirilebilir. Dört boyutlu Kartezyen koordinatları ( w , x , y , z ) olarak gösterilsin , burada ( x , y , z ) normal konum vektörü r'nin Kartezyen koordinatlarını temsil eder . Üç boyutlu momentum vektörü p , üç boyutlu bir birim küre üzerinde dört boyutlu bir vektör ile ilişkilidir.${\displaystyle {\boldsymbol {\eta }}}$

${\displaystyle {\begin{aligned}{\boldsymbol {\eta }}&=\displaystyle {\frac {p^{2}-p_{0}^{2}}{p^{2}+p_{0 }^{2}}}\mathbf {\hat {w}} +{\frac {2p_{0}}{p^{2}+p_{0}^{2}}}\mathbf {p} \\ [1em]&=\displaystyle {\frac {mk-rp_{0}^{2}}{mk}}\mathbf {\hat {w}} +{\frac {rp_{0}}{mk}}\ mathbf {p} ,\end{hizalı}}}$

yeni w ekseni boyunca birim vektör nerede . Dönüşüm eşleme s için r | benzersiz tersine çevrilebilir; örneğin, momentumun x bileşeni eşittir ${\displaystyle \mathbf {\hat {w}} }$

${\displaystyle p_{x}=p_{0}{\frac {\eta _{x}}{1-\eta _{w}}},}$

ve benzer şekilde p _y ve p _{z için} . Başka bir deyişle, üç boyutlu vektör p , dört boyutlu vektörün p _{0 ile} ölçeklenen bir stereografik izdüşümüdür (Şekil 8). ${\displaystyle {\boldsymbol {\eta }}}$

Genelliği kaybetmeden, Kartezyen koordinatları, z ekseni L açısal momentum vektörü ile hizalanacak ve momentum hodografları Şekil 7'deki gibi hizalanacak şekilde, dairelerin merkezleri üzerinde olacak şekilde seçerek normal dönme simetrisini ortadan kaldırabiliriz . y ekseni. Hareket düzlemsel ve olduğu p ve L dik olan p _z = η _z = 0 ve dikkat üç boyutlu vektöre sınırlanabilir = ( r | _a , η _X , η _y ) . Apollon momentum hodograf daireleri ailesi (Şekil 7) üç boyutlu küre üzerindeki büyük dairelerin bir ailesine karşılık gelir ve bunların tümü momentum hodograf odaklarına karşılık gelen iki odakta η _x eksenini keser η _x = ±1 de p _x = ± p ₀ . Bu büyük daireler, η _x ekseni etrafında basit bir dönüşle ilişkilidir (Şekil 8). Bu dönme simetrisi, aynı enerjinin tüm yörüngelerini birbirine dönüştürür; dördüncü boyut dönüştürür bununla birlikte, bu tür bir döndürme, genellikle üç boyutlu dönme ortogonal olan r _a . Bu yüksek simetri Kepler probleminin karakteristiğidir ve LRL vektörünün korunumuna karşılık gelir. ${\displaystyle {\boldsymbol {\eta }}}$${\displaystyle {\boldsymbol {\eta }}}$

Eliptik silindirik koordinatlar ( χ , ψ , φ ) lehine fazlalık dört boyutlu koordinatları ortadan kaldırarak Kepler problemi için zarif bir hareket açısı değişkenleri çözümü elde edilebilir.${\displaystyle {\boldsymbol {\eta }}}$

${\displaystyle \eta _{w}=\operatöradı {cn} \chi \operatöradı {cn} \psi ,}$

${\displaystyle \eta _{x}=\operatöradı {sn} \,\chi \operatöradı {dn} \psi \,\cos \phi ,}$

${\displaystyle \eta _{y}=\operatöradı {sn} \chi \operatöradı {dn} \psi \sin \phi ,}$

${\displaystyle \eta _{z}=\operatöradı {dn} \chi \operatöradı {sn} \psi ,}$

burada sn, cn ve dn Jacobi'nin eliptik fonksiyonlarıdır .

Diğer potansiyeller ve görelilik için genellemeler

Laplace–Runge–Lenz vektörü, diğer durumlar için geçerli olan korunan miktarları belirlemek için de genelleştirilebilir.

Düzgün bir elektrik alanı varlığında, E , genelleştirilmiş Laplace-Runge Lenz vektörü olan ${\görüntüleme stili {\matematiksel {A}}}$

${\displaystyle {\mathcal {A}}=\mathbf {A} +{\frac {mq}{2}}\left[\left(\mathbf {r} \times \mathbf {E} \sağ)\times \mathbf {r} \sağ],}$

burada q, olan yük etrafında dönen parçacığın. Korunmamasına rağmen , korunan bir niceliğe, yani . ${\görüntüleme stili {\matematiksel {A}}}$${\displaystyle {\mathcal {A}}\cdot \mathbf {E} }$

Laplace–Runge–Lenz vektörünü diğer potansiyellere ve özel göreliliğe daha da genelleştirerek, en genel form şu şekilde yazılabilir:

${\displaystyle {\mathcal {A}}=\left({\frac {\partial \xi }{\partial u}}\right)\left(\mathbf {p} \times \mathbf {L} \sağ) +\left[\xi -u\left({\frac {\partial \xi }{\partial u}}\sağ)\sağ]L^{2}\mathbf {\hat {r}} ,}$

burada u = 1/ r ve ξ = cos θ , θ açısı ile tanımlanır

${\displaystyle \theta =L\int ^{u}{\frac {du}{\sqrt {m^{2}c^{2}(\gamma ^{2}-1)-L^{2}u ^{2}}}},}$

ve γ ise Lorentz faktörü . Daha önce olduğu gibi , korunan açısal momentum vektörü ile çapraz ürünü alarak korunmuş bir binormal B vektörü elde edebiliriz.

${\displaystyle {\mathcal {B}}=\mathbf {L} \times {\mathcal {A}}.}$

Bu iki vektör aynı şekilde korunan bir ikili tensör W ile birleştirilebilir ,

${\displaystyle {\mathcal {W}}=\alpha {\mathcal {A}}\otimes {\mathcal {A}}+\beta \,{\mathcal {B}}\otimes {\mathcal {B}} .}$

Örnekte, göreli olmayan, izotropik harmonik osilatör için LRL vektörü hesaplanabilir. Kuvvet merkezi olduğundan,

${\displaystyle \mathbf {F} (r)=-k\mathbf {r} ,}$

açısal momentum vektörü korunur ve hareket bir düzlemdedir.

Korunmuş ikili tensör basit bir biçimde yazılabilir

${\displaystyle {\mathcal {W}}={\frac {1}{2m}}\mathbf {p} \otimes \mathbf {p} +{\frac {k}{2}}\,\mathbf {r } \otimes \mathbf {r} ,}$

Her ne kadar p ve r, mutlaka dikey değildir.

Karşılık gelen Runge–Lenz vektörü daha karmaşıktır,

${\displaystyle {\mathcal {A}}={\frac {1}{\sqrt {mr^{2}\omega _{0}A-mr^{2}E+L^{2}}}}\ sol\{\left(\mathbf {p} \times \mathbf {L} \sağ)+\left(mr\omega _{0}A-mrE\sağ)\mathbf {\hat {r}} \sağ\ },}$

nerede

${\displaystyle \omega _{0}={\sqrt {\frac {k}{m}}}}$

doğal salınım frekansıdır ve

${\displaystyle A=(E^{2}-\omega ^{2}L^{2})^{1/2}/\omega .}$

Kepler problemlerinde Laplace–Runge–Lenz vektörünün korunduğunun kanıtları

Aşağıdakiler, LRL vektörünün bir ters kare yasasına uyan merkezi kuvvetler altında korunduğunu gösteren argümanlardır.

Korumanın doğrudan kanıtı

Parçacığa etkiyen merkezi bir kuvvet , ${\görüntüleme stili \mathbf {F} }$

${\displaystyle \mathbf {F} ={\frac {d\mathbf {p} }{dt}}=f(r){\frac {\mathbf {r} }{r}}=f(r)\mathbf {\hat {r}} }$

yarıçapın bir fonksiyonu için . Açısal momentum merkezi kuvvetler altında korunduğundan ve ${\görüntüleme stili f(r)}$${\görüntüleme stili r}$${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }$${\displaystyle {\frac {d}{dt}}\mathbf {L} =0}$

${\displaystyle {\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \sağ)={\frac {d\mathbf {p} }{dt}}\times \ mathbf {L} =f(r)\mathbf {\hat {r}} \times \left(\mathbf {r} \times m{\frac {d\mathbf {r} }{dt}}\sağ)= f(r){\frac {m}{r}}\left[\mathbf {r} \left(\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}\sağ) -r^{2}{\frac {d\mathbf {r} }{dt}}\sağ],}$

momentumun ve üçlü çapraz çarpımın Lagrange formülü kullanılarak basitleştirildiği yer${\displaystyle \mathbf {p} =m{\frac {d\mathbf {r} }{dt}}}$

${\displaystyle \mathbf {r} \times \left(\mathbf {r} \times {\frac {d\mathbf {r} }{dt}}\sağ)=\mathbf {r} \left(\mathbf { r} \cdot {\frac {d\mathbf {r} }{dt}}\sağ)-r^{2}{\frac {d\mathbf {r} }{dt}}.}$

Kimlik

${\displaystyle {\frac {d}{dt}}\left(\mathbf {r} \cdot \mathbf {r} \sağ)=2\mathbf {r} \cdot {\frac {d\mathbf {r} }{dt}}={\frac {d}{dt}}(r^{2})=2r{\frac {dr}{dt}}}$

denklemi verir

${\displaystyle {\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \sağ)=-mf(r)r^{2}\left[{\frac {1 }{r}}{\frac {d\mathbf {r} }{dt}}-{\frac {\mathbf {r} }{r^{2}}}{\frac {dr}{dt}}\ sağ]=-mf(r)r^{2}{\frac {d}{dt}}\left({\frac {\mathbf {r} }{r}}\sağ).}$

Bir ters kare merkez kuvvetinin özel durumu için , bu eşittir ${\displaystyle f(r)={\frac {-k}{r^{2}}}}$

${\displaystyle {\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \sağ)=mk{\frac {d}{dt}}\left({\frac { \mathbf {r} }{r}}\sağ)={\frac {d}{dt}}(mk\mathbf {\hat {r}} ).}$

Bu nedenle, A ters kare merkezi kuvvetler için korunur

${\displaystyle {\frac {d}{dt}}\mathbf {A} ={\frac {d}{dt}}\left(\mathbf {p} \times \mathbf {L} \sağ)-{\ frac {d}{dt}}\left(mk\mathbf {\hat {r}} \sağ)=\mathbf {0} .}$

Açısal momentumun açısal hız ile ilişkisi kullanılarak daha kısa bir kanıt elde edilir , bu da 'ye dik bir düzlemde hareket eden bir parçacık için geçerlidir . Ters-kare, merkezi kuvvetlere belirtme, zamana göre türevi IS ${\displaystyle \mathbf {L} =mr^{2}{\boldsymbol {\omega }}}$${\displaystyle \mathbf {L} }$${\displaystyle \mathbf {p} \times \mathbf {L} }$

${\displaystyle {\frac {d}{dt}}\mathbf {p} \times \mathbf {L} =\left({\frac {-k}{r^{2}}}\mathbf {\hat { r}} \sağ)\times \left(mr^{2}{\boldsymbol {\omega }}\right)=mk\,{\boldsymbol {\omega }}\times \mathbf {\hat {r}} =mk\,{\frac {d}{dt}}\mathbf {\hat {r}} ,}$

burada son eşitlik geçerlidir, çünkü bir birim vektör yalnızca dönüşle değişebilir ve dönen vektörün yörünge hızıdır. Böylece A , eşit zaman türevlerine sahip iki vektörün farkı olarak görülür. ${\displaystyle {\boldsymbol {\omega }}\times \mathbf {\hat {r}} }$

Bu makalenin başka bir yerinde açıklandığı gibi , bu LRL vektörü A , tüm merkezi kuvvetler için tanımlanabilen bir genel korunmuş vektörün özel bir durumudur . Bununla birlikte, çoğu merkezi kuvvet kapalı yörüngeler üretmediğinden (bkz. Bertrand teoremi ), benzer vektör nadiren basit bir tanıma sahiptir ve genellikle r ile θ arasındaki açının çok değerli bir fonksiyonudur . ${\görüntüleme stili {\matematiksel {A}}}$${\görüntüleme stili {\matematiksel {A}}}$${\görüntüleme stili {\matematiksel {A}}}$

Parabolik koordinatlarda Hamilton-Jacobi denklemi

LRL vektörünün sabitliği, denklemlerle tanımlanan parabolik koordinatlarda ( ξ , η ) Hamilton-Jacobi denkleminden de türetilebilir.

${\görüntüleme stili \xi =r+x,}$

${\görüntüleme stili \eta =rx,}$

burada r yörünge düzlemindeki yarıçapı temsil eder

${\displaystyle r={\sqrt {x^{2}+y^{2}}}.}$

Bu koordinatların ters çevrilmesi

${\displaystyle x={\frac {1}{2}}(\xi -\eta ),}$

${\displaystyle y={\sqrt {\xi \eta }},}$

Hamilton-Jacobi denkleminin bu koordinatlarda ayrılması, iki eşdeğer denklemi verir.

${\displaystyle 2\xi p_{\xi }^{2}-mk-mE\xi =-\Gamma,}$

${\displaystyle 2\eta p_{\eta }^{2}-mk-mE\eta =\Gama ,}$

burada Γ bir hareket sabitidir. Kartezyen momentum p _x ve p _y cinsinden çıkarma ve yeniden ifade , Γ'nin LRL vektörüne eşdeğer olduğunu gösterir.

${\displaystyle \Gamma =p_{y}(xp_{y}-yp_{x})-mk{\frac {x}{r}}=A_{x}.}$

Noether teoremi

Yukarıda açıklanan dönme simetrisi ile LRL vektörünün korunumu arasındaki bağlantı, Noether teoremi yoluyla nicel yapılabilir . Hareket sabitlerini bulmak için kullanılan bu teorem, fiziksel bir sistemin genelleştirilmiş koordinatlarının herhangi bir sonsuz küçük varyasyonunun

${\displaystyle \delta q_{i}=\varepsilon g_{i}(\mathbf {q} ,\mathbf {\dot {q}} ,t)}$

bu, Lagrange'ın toplam zaman türevi ile birinci dereceden değişmesine neden olur.

${\displaystyle \delta L=\varepsilon {\frac {d}{dt}}G(\mathbf {q} ,t)}$

korunan bir miktara karşılık gelir Γ

${\displaystyle \Gamma =-G+\sum _{i}g_{i}\left({\frac {\partial L}{\partial {\dot {q}}_{i}}}\sağ).}$

Özellikle, korunan LRL vektör bileşeni A _s , koordinatlardaki varyasyona karşılık gelir.

${\displaystyle \delta _{s}x_{i}={\frac {\varepsilon }{2}}\left[2p_{i}x_{s}-x_{i}p_{s}-\delta _{ is}\sol(\mathbf {r} \cdot \mathbf {p} \sağ)\sağ],}$

burada i ile 1, 2 ve 3'e eşit x _i ve p _ı olmak i konum ve momentum vektörlerinin inci bileşenler r ve p sırasıyla; Her zamanki gibi, δ _edilir temsil Kronecker'in delta . Lagrange'da ortaya çıkan birinci dereceden değişiklik,

${\displaystyle \delta L={\frac {1}{2}}\varepsilon mk{\frac {d}{dt}}\sol({\frac {x_{s}}{r}}\sağ). }$

Korunan miktar Γ için genel formülde ikame , LRL vektörünün korunan A _s bileşenini verir ,

${\displaystyle A_{s}=\left[p^{2}x_{s}-p_{s}\ \left(\mathbf {r} \cdot \mathbf {p} \sağ)\sağ]-mk\ sol({\frac {x_{s}}{r}}\sağ)=\left[\mathbf {p} \times \left(\mathbf {r} \times \mathbf {p} \sağ)\sağ] _{s}-mk\sol({\frac {x_{s}}{r}}\sağ).}$

yalan dönüşümü

Şekil 9: LRL vektörü A'nın korunumunun türetildiği Lie dönüşümü . Ölçekleme parametresi λ değiştikçe, enerji ve açısal momentum değişir, ancak dışmerkezlik e ve A'nın büyüklüğü ve yönü değişmez .

Noether teoremi türev OML vektör korunumu A zarif, ancak bir dezavantajı var koordinat değişim Ax _i sadece içeren pozisyon r değil, aynı zamanda moment p eşdeğer ya da, hız v . Bu dezavantaj, bunun yerine Sophus Lie'nin öncülük ettiği bir yaklaşım kullanılarak A'nın korunumunun türetilmesiyle ortadan kaldırılabilir . Spesifik olarak, r koordinatlarının ve t zamanının bir parametre λ'nın farklı güçleri tarafından ölçeklendiği bir Lie dönüşümü tanımlanabilir (Şekil 9),

${\displaystyle t\rightarrow \lambda ^{3}t,\qquad \mathbf {r} \rightarrow \lambda ^{2}\mathbf {r} ,\qquad \mathbf {p} \rightarrow {\frac {1} {\lambda }}\mathbf {p} .}$

Bu dönüşüm toplam açısal momentumu L ve enerjiyi E değiştirir ,

${\displaystyle L\rightarrow \lambda L,\qquad E\rightarrow {\frac {1}{\lambda ^{2}}}E,}$

ancak ürünlerini EL ² korur . Bu nedenle, eksantriklik e ve büyüklüğü bir korunur, hem de görüleceği üzere denklem A ²

${\displaystyle A^{2}=m^{2}k^{2}e^{2}=m^{2}k^{2}+2mEL^{2}.}$

A'nın yönü de korunur, çünkü yarı eksenler küresel bir ölçekleme tarafından değiştirilmez. Bu dönüşüm aynı zamanda Kepler'in üçüncü yasasını da korur , yani yarım eksen a ve T periyodu bir sabit  T ² / a ^{3 oluşturur} .

Alternatif ölçekler, semboller ve formülasyonlar

Momentum ve açısal momentum vektörleri p ve L'den farklı olarak, Laplace–Runge–Lenz vektörünün evrensel olarak kabul edilmiş bir tanımı yoktur; bilimsel literatürde birkaç farklı ölçeklendirme faktörü ve sembol kullanılmaktadır. En yaygın tanım yukarıda verilmiştir , ancak diğer bir yaygın alternatif, boyutsuz korunmuş bir dışmerkezlik vektörü elde etmek için mk sabitine bölmektir.

${\displaystyle \mathbf {e} ={\frac {1}{mk}}\left(\mathbf {p} \times \mathbf {L} \sağ)-\mathbf {\hat {r}} ={\ frac {m}{k}}\left(\mathbf {v} \times \left(\mathbf {r} \times \mathbf {v} \sağ)\sağ)-\mathbf {\hat {r}} , }$

burada v hız vektörüdür. Bu ölçeklendirilmiş vektör e , A ile aynı yöne sahiptir ve büyüklüğü yörüngenin dış merkezliliğine eşittir ve dolayısıyla dairesel yörüngeler için kaybolur.

Diğer ölçekli versiyonları bölünerek, örneğin, aynı zamanda mümkündür A tarafından m , tek başına

${\displaystyle \mathbf {M} =\mathbf {v} \times \mathbf {L} -k\mathbf {\hat {r}} ,}$

veya p _{0 ile}

${\displaystyle \mathbf {D} ={\frac {\mathbf {A} }{p_{0}}}={\frac {1}{\sqrt {2m|E|}}}\left\{\mathbf {p} \times \mathbf {L} -mk\mathbf {\hat {r}} \sağ\},}$

açısal momentum vektörü L ile aynı birimlere sahiptir .

Nadir durumlarda, LRL vektörünün işareti tersine çevrilebilir, yani -1 ile ölçeklenebilir. LRL vektörü için diğer yaygın semboller arasında a , R , F , J ve V bulunur . Ancak, LRL vektörü için ölçeklendirme ve sembol seçimi, onun korunmasını etkilemez.

Şekil 4: Açısal momentum vektörü L , LRL vektörü A ve Hamilton vektörü, binormal B , karşılıklı olarak diktir; A ve B , Kepler probleminin eliptik yörüngesinin sırasıyla büyük ve küçük eksenleri boyunca işaret eder.

Alternatif bir korunan vektör, William Rowan Hamilton tarafından incelenen binormal B vektörüdür ,

korunmuş olan ve elipsin küçük yarım ekseni boyunca işaret eden. (Eksantrikliğin kaybolması için tanımlanmamıştır.)

LRL vektörü A = B × L , B ve L' nin çapraz ürünüdür (Şekil 4). Yukarıdaki ilgili bölümdeki momentum hodografında, B'nin momentumun başlangıcını dairesel hodografın merkezine bağladığı ve A/L büyüklüğüne sahip olduğu kolaylıkla görülmektedir . Perihelion'da, momentum yönünü gösterir.

Vektör B her iki dik olduğu "binormalli" olarak ifade edilmektedir , A ve L . LRL vektörünün kendisine benzer şekilde, binormal vektör de farklı ölçekler ve sembollerle tanımlanabilir.

İki korunan vektör, A ve B , korunan bir ikili tensör W oluşturmak için birleştirilebilir ,

${\displaystyle \mathbf {W} =\alpha \mathbf {A} \otimes \mathbf {A} +\beta \,\mathbf {B} \otimes \mathbf {B} ,}$

burada α ve β keyfi ölçekleme sabitleridir ve tensör çarpımını temsil eder ( benzer sembollerine rağmen vektör çapraz çarpımı ile ilgili değildir ). Açık bileşenlerde yazılmış bu denklem okur ${\görüntüleme stili \ bazen }$

${\displaystyle W_{ij}=\alpha A_{i}A_{j}+\beta B_{i}B_{j}.}$

Birbirlerine dik olduklarından, A ve B vektörleri , korunan tensör W'nin , yani onun ölçeklenmiş özvektörlerinin ana eksenleri olarak görülebilir . W , L'ye diktir ,

${\displaystyle \mathbf {L} \cdot \mathbf {W} =\alpha \left(\mathbf {L} \cdot \mathbf {A} \sağ)\mathbf {A} +\beta \left(\mathbf { L} \cdot \mathbf {B} \sağ)\mathbf {B} =0,}$

çünkü bir ve B her ikisi de dik olan L yanı sıra, L ⋅ bir = L ⋅ B = 0 .

Daha doğrudan, bu denklem, açık bileşenlerde okur,

${\displaystyle \left(\mathbf {L} \cdot \mathbf {W} \sağ)_{j}=\alpha \left(\sum _{i=1}^{3}L_{i}A_{i }\right)A_{j}+\beta \left(\sum _{i=1}^{3}L_{i}B_{i}\sağ)B_{j}=0.}$

Ayrıca bakınız

• Astrodinamik : Yörünge , Eksantriklik vektörü , Yörünge elemanları
• Bertrand teoremi
• binet denklemi
• İki cisim sorunu

Referanslar

daha fazla okuma

• Baez, John (2008). "Kepler Problemi Yeniden Gözden Geçirildi: Laplace–Runge–Lenz Vektörü" (PDF) . 2021-05-31 alındı .
• Baez, John (2003). "Yerçekimi 2 cisim sorununun gizemleri" . Arşivlenmiş orijinal 2008-10-21 tarihinde . 2004-12-11 alındı .
• Baez, John (2018). "Yerçekimi 2 cisim sorununun gizemleri" . 2021-05-31 alındı . Önceki kaynağın güncellenmiş versiyonu.
• D'Eliseo, MM (2007). "Birinci dereceden yörünge denklemi". Amerikan Fizik Dergisi . 75 (4): 352–355. Bibcode : 2007AmJPh..75..352D . doi : 10.1119/1.2432126 .
• Hall, Brian C. (2013), Matematikçiler için Kuantum Teorisi, Matematikte Lisansüstü Metinler, 267 , Springer, ISBN 978-461471158.
• Leach, PGL; GP Flessas (2003). "Laplace–Runge–Lenz vektörünün genellemeleri". J. Doğrusal Olmayan Matematik. Fizik . 10 (3): 340–423. arXiv : matematik-ph/0403028 . Bibcode : 2003JNMP...10..340L . doi : 10.2991/jnmp.2003.10.3.6 . S2CID  73707398 .