Jacobi eliptik fonksiyonları - Jacobi elliptic functions

In matematik , Jacobi eliptik fonksiyonlar temel kümesidir eliptik fonksiyonlar , ve yardımcı teta fonksiyonları tarihi öneme sahip olduğunu,. Bir sarkacın hareketinin tanımında (ayrıca bkz. sarkaç (matematik) ) ve elektronik eliptik filtrelerin tasarımında bulunurlar . Da trigonometrik fonksiyonlar bir çevreye referansla tanımlandığı gibidir, Jacobi eliptik işlevleri diğer bakın bir genelleme olarak konik kesitler , özellikle elips. Trigonometrik fonksiyonlarla olan ilişki, gösterimde, örneğin eşleşen gösterimde bulunur.${\ Displaystyle \ operatör adı {sn} }$için . Jacobi eliptik fonksiyonları, karmaşık analiz kavramlarının tanımlanmasını ve/veya anlaşılmasını gerektirmediklerinden , Weierstrass eliptik fonksiyonlarına göre pratik problemlerde daha sık kullanılır . Carl Gustav Jakob Jacobi  ( 1829 ) tarafından tanıtıldılar . ${\görüntüleme stili\sin }$

genel bakış

Karmaşık düzlemdeki temel dikdörtgen ${\görüntüleme stili u}$

, , , ve harflerinin herhangi birinin nerede olduğu ve nerede olduğu ile gösterilen on iki Jacobi eliptik işlevi vardır . (Formun işlevleri, notasyonel tamlık için önemsiz bir şekilde birliğe ayarlanmıştır.) argümandır ve her ikisi de karmaşık olabilen parametredir. ${\görüntüleme stili \operatöradı {pq} (u,m)}$${\görüntüleme stili \mathrm {p} }$${\görüntüleme stili \mathrm {q} }$${\görüntüleme stili \mathrm {c} }$${\görüntüleme stili \mathrm {s} }$${\görüntüleme stili \mathrm {n} }$${\görüntüleme stili \mathrm {d} }$${\displaystyle \operatöradı {pp} (u,m)}$${\görüntüleme stili u}$${\görüntüleme stili m}$

Argümanın karmaşık düzleminde , on iki fonksiyon, basit kutuplar ve sıfırlardan oluşan tekrar eden bir kafes oluşturur . Fonksiyonu, bir tekrar eden paralelkenar ya da birim hücre bağlı olarak, uzunluk tarafa sahip olabilir ya da gerçek eksende ve ya hayali eksen üzerinde ve şekilde bilinmektedir Çeyrek dönemler ile olmak eliptik yekpare birinci tür. Birim hücrenin doğası , bir köşede orijin tarafından oluşturulan bir dikdörtgen olan ve çapraz olarak zıt köşe olan "yardımcı dikdörtgen" (genellikle bir paralelkenar) incelenerek belirlenebilir . Şemada olduğu gibi, yardımcı dikdörtgenin dört köşesi , orijinden saat yönünün tersine hareket ederek , , , ve olarak adlandırılır . Fonksiyonun köşesinde bir sıfır ve köşede bir direğe sahip olacaktır . On iki fonksiyon, bu kutupları ve sıfırları dikdörtgenin köşelerinde düzenlemenin on iki yoluna karşılık gelir. ${\görüntüleme stili u}$${\ Displaystyle 2K}$${\görüntüleme stili 4K}$${\ Displaystyle 2K'}$${\ Displaystyle 4K'}$${\görüntüleme stili K=K(m)}$${\görüntüleme stili K'=K(1-m)}$${\ Displaystyle K(\cdot )}$${\görüntüleme stili (0,0)}$${\görüntüleme stili (K,K')}$${\görüntüleme stili \mathrm {s} }$${\görüntüleme stili \mathrm {c} }$${\görüntüleme stili \mathrm {d} }$${\görüntüleme stili \mathrm {n} }$${\görüntüleme stili \operatöradı {pq} (u,m)}$${\görüntüleme stili \mathrm {p} }$${\görüntüleme stili \mathrm {q} }$

Argüman ve parametre gerçek olduğunda , ve ile gerçek olacak ve yardımcı paralelkenar aslında bir dikdörtgen olacak ve Jacobi eliptik fonksiyonlarının tümü gerçek çizgide gerçek değerli olacaktır. ${\görüntüleme stili u}$${\görüntüleme stili m}$${\görüntüleme stili 0<m<1}$${\görüntüleme stili K}$${\görüntüleme stili K'}$

Matematiksel olarak, Jacobian eliptik fonksiyonlar , karmaşık düzlemde iki kat periyodik meromorfik fonksiyonlardır . İki kat periyodik olduklarından, bir simit aracılığıyla çarpanlara ayrılırlar - aslında, kosinüs ve sinüsün gerçekte bir daire üzerinde tanımlandığı gibi, etki alanları bir simit olarak alınabilir. Sadece bir daireye sahip olmak yerine, şimdi biri gerçek diğeri hayali olan iki dairenin çarpımına sahibiz. Karmaşık düzlem, karmaşık bir torus ile değiştirilebilir . Çemberin çevresi olan ve ikinci , ve vardır çeyrek süreleri . Her fonksiyonun torus üzerinde zıt konumlarda iki sıfırı ve iki kutbu vardır. , , , noktaları arasında bir sıfır ve bir kutup vardır. ${\görüntüleme stili 4K}$${\ Displaystyle 4K'}$${\görüntüleme stili K}$${\görüntüleme stili K'}$${\görüntüleme stili 0}$${\görüntüleme stili K}$${\displaystyle K+iK'}$${\görüntüleme stili iK'}$

Jacobian eliptik fonksiyonlar daha sonra aşağıdaki üç özelliği karşılayan benzersiz çift periyodik, meromorfik fonksiyonlardır:

• Köşede basit bir sıfır ve köşede basit bir direk var  .${\görüntüleme stili \mathrm {p} }$${\görüntüleme stili \mathrm {q} }$
• Gelen adım için fonksiyonun yarım dönemine eşittir ; olduğu, fonksiyon yönünde periyodik iki kez mesafe olan süre ile birlikte, için . Fonksiyon ayrıca diğer iki yönde de periyodiktir , diğer köşelerden birine olan mesafe çeyrek periyot olacak şekilde bir periyot vardır.${\görüntüleme stili \mathrm {p} }$${\görüntüleme stili \mathrm {q} }$${\displaystyle \operatöradı {pq} u}$${\displaystyle \operatöradı {pq} u}$${\displaystyle \operatör adı {pq} }$${\görüntüleme stili \mathrm {p} }$${\görüntüleme stili \mathrm {q} }$${\displaystyle \operatöradı {pq} u}$${\görüntüleme stili \mathrm {p} }$
• Fonksiyon köşelerden birinde cinsinden genişletilirse , genişlemedeki öncü terimin katsayısı  . Başka bir deyişle, genişletilmesi başterim köşesi de olduğu ; köşesinde genleşme başterim olan ve diğer iki köşe bir genleşme gelen bir terimdir  .${\displaystyle \operatöradı {pq} u}$${\görüntüleme stili u}$${\görüntüleme stili 1}$${\displaystyle \operatöradı {pq} u}$${\görüntüleme stili \mathrm {p} }$${\görüntüleme stili u}$${\görüntüleme stili \mathrm {q} }$${\ Displaystyle u^{-1}}$${\görüntüleme stili 1}$

Jacobi eliptik işlevi ${\ Displaystyle \ operatör adı {sn} }$

Jacobi eliptik işlevi ${\ Displaystyle \ operatör adı {cn} }$

Jacobi eliptik işlevi ${\ Displaystyle \ operatör adı {dn} }$

Jacobi eliptik işlevi ${\görüntüleme stili \operatör adı {sc} }$

Karmaşık düzlemde dört Jacobi Eliptik Fonksiyonun çift ​​periyodik davranışlarını gösteren çizimleri. Etki alanı renklendirme yönteminin bir sürümü kullanılarak oluşturulan resimler . Hepsinin parametre değerleri eşittir .${\görüntüleme stili u}$${\görüntüleme stili k}$${\görüntüleme stili 0.8}$

gösterim

Eliptik fonksiyonlar, konuyu gereksiz yere kafa karıştırıcı hale getirebilecek çeşitli notasyonlarda verilebilir. Eliptik fonksiyonlar iki değişkenli fonksiyonlardır. İlk değişken, genlik cinsinden veya daha yaygın olarak aşağıda verilen terimlerle verilebilir. İkinci değişken açısından verilmiş olabilir parametresi , ya da eliptik modülü , veya anlamında modüler açısı burada, . Tamamlayıcıları ve tanımlandığı gibidir ve . Bu dört terim, çeşitli ifadeleri basitleştirmek için aşağıda yorum yapılmadan kullanılmıştır. ${\görüntüleme stili \varphi }$${\görüntüleme stili u}$ ${\görüntüleme stili m}$ ${\görüntüleme stili k}$${\görüntüleme stili k^{2}=m}$ ${\görüntüleme stili \alfa }$${\displaystyle m=\sin ^{2}\alpha }$${\görüntüleme stili k}$${\görüntüleme stili m}$${\görüntüleme stili m'=1-m}$${\textstyle k'={\sqrt {m'}}}$

Oniki Jacobi eliptik fonksiyonlar genelde yazılır nerede ve harflerin herhangi biri , , , ve . Formun işlevleri, notasyonel tamlık için önemsiz bir şekilde birliğe ayarlanır. “Majör” işlevleri genellikle olmaya alınır , ve hangi diğer tüm fonksiyonlar elde edilebilir ve ifadeler genellikle bu üç işlevleri açısından yalnızca yazılır, ancak, çeşitli simetriler ve genellemeler genellikle en uygun tam seti kullanılarak ifade edilir. (Bu gösterim Gudermann ve Glaisher'a aittir ve Jacobi'nin orijinal gösterimi değildir.) ${\görüntüleme stili \operatöradı {pq} (u,m)}$${\görüntüleme stili \mathrm {p} }$${\görüntüleme stili \mathrm {q} }$${\görüntüleme stili \mathrm {c} }$${\görüntüleme stili \mathrm {s} }$${\görüntüleme stili \mathrm {n} }$${\görüntüleme stili \mathrm {d} }$${\displaystyle \operatöradı {pp} (u,m)}$${\görüntüleme stili \operatör adı {cn} (u,m)}$${\displaystyle \operatöradı {sn} (u,m)}$${\displaystyle \operatör adı {dn} (u,m)}$

parametre

Fonksiyonlar, çarpım kuralı ile notasyonel olarak birbirleriyle ilişkilidir: (argümanlar bastırılır)

${\displaystyle \operatöradı {pq} \cdot \operatöradı {p'q'} =\operatöradı {pq'} \cdot \operatöradı {p'q} }$

hangi yaygın olarak kullanılan diğer ilişkiler türetilebilir:

${\displaystyle {\frac {\operatöradı {pr} }{\operatöradı {qr} }}=\operatöradı {pq} }$

${\displaystyle \operatöradı {pr} \cdot \operatöradı {rq} =\operatöradı {pq} }$

${\displaystyle {\frac {1}{\operatöradı {qp} }}=\operatöradı {pq} }$

Çarpma kuralı, eliptik fonksiyonların Neville teta fonksiyonlarıyla tanımlanmasından hemen sonra gelir.

${\displaystyle \operatöradı {pq} (u,m)={\frac {\theta _{\operatöradı {p} }(u,m)}{\theta _{\operatöradı {q} }(u,m) }}}$

Eliptik integrallerin tersi olarak tanım

Bağımsız değişkenler u ve k'nin bir fonksiyonu olarak genlik modeli (dikey eksen boyunca ölçülür)

Belirli özellikleri karşılayan benzersiz meromorfik fonksiyonlar açısından yukarıdaki tanım oldukça soyuttur. Eliptik fonksiyonları birinci türden eksik eliptik integralin tersi olarak veren daha basit ama tamamen eşdeğer bir tanım vardır . İzin vermek

${\displaystyle u=\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {1-m\sin ^{2}\theta }}}}\,.}$

Daha sonra eliptik sinüs sn  u (Latince: sinüs amplitudinis ) ile verilir

${\displaystyle \operatöradı {sn} u=\sin \varphi \,}$

ve eliptik kosinüs cn  u (Latince: cosinus amplitudinis ) ile verilir

${\displaystyle \operatör adı {cn} u=\cos \varphi }$

ve delta genliği dn  u (Latince: delta amplitudinis )

${\displaystyle \operatöradı {dn} u={\sqrt {1-m\sin ^{2}\varphi }}\,.}$

Burada açıya genlik denir . Bazen delta genliği olarak adlandırılır . Yukarıda, değer , genellikle real olarak alınan serbest bir parametredir ve dolayısıyla eliptik fonksiyonların genlik ve parametre  olmak üzere iki değişken tarafından verildiği düşünülebilir . ${\görüntüleme stili \varphi }$${\displaystyle \operatör adı {dn} u=\Delta (u)}$${\görüntüleme stili m}$${\displaystyle 0\leq m\leq 1}$${\görüntüleme stili \varphi }$${\görüntüleme stili m}$

Kalan dokuz eliptik fonksiyon, yukarıdaki üçten kolayca oluşturulur ve aşağıdaki bir bölümde verilmiştir.

Ne zaman , u'nun çeyrek döneme eşit olduğuna dikkat edin . ${\displaystyle \varphi =\pi /2}$ ${\görüntüleme stili K}$

Trigonometri olarak tanım: Jacobi elipsi

φ açısı ve b parametresinin belirli değerleri için Jacobi elipsinin ( x ² + y ² /b ² =1, b gerçek) ve on iki Jacobi Eliptik fonksiyonunun pq(u,m) grafiği . Katı eğrisi ile elips m = 1-1 / b ² ve u = F (φ, m) , F (.,.) Olan eliptik yekpare birinci tür. Noktalı eğri birim çemberdir. dc'de x eksenini kesen x=cd noktasındaki daire ve elipsin teğet çizgileri açık gri renkte gösterilmiştir.

${\displaystyle \cos \varphi ,\sin \varphi }$pozitif x ekseninden ölçülen birim çemberin yarıçapı r  = 1 ve açı yay uzunluğu ile birim çember üzerinde tanımlanır . Benzer şekilde, Jacobi eliptik fonksiyonları birim elips üzerinde a  = 1 ile tanımlanır.${\görüntüleme stili \varphi =}$

${\displaystyle {\begin{aligned}&x^{2}+{\frac {y^{2}}{b^{2}}}=1,\quad b>1,\\&m=1-{\ frac {1}{b^{2}}},\quad 0<m<1,\\&x=r\cos \varphi ,\quad y=r\sin \varphi \end{aligned}}}$

sonra:

${\displaystyle r(\varphi ,m)={\frac {1}{\sqrt {1-m\sin ^{2}\varphi }}}\,.}$

Her açı için parametre ${\görüntüleme stili \varphi }$

${\displaystyle u=u(\varphi ,m)=\int _{0}^{\varphi }r(\theta ,m)\,d\theta }$

hesaplanır. Birim çemberde ( ), bir yay uzunluğu olacaktır. İken eliptik durumda doğrudan geometrik yorumunu taşımak görünmüyor, bu eliptik fonksiyonların tanımını girer parametre olarak çıkıyor. Gerçekten de, izin elips üzerinde bir nokta olması ve izin birim çember arasındaki çizgi kestiği nokta olarak ve kökeni . Sonra birim çemberden tanıdık ilişkiler: ${\görüntüleme stili a=b=1}$${\görüntüleme stili u}$${\görüntüleme stili u}$${\displaystyle P=(x,y)=(r\cos \varphi ,r\sin \varphi )}$${\displaystyle P'=(x',y')=(\cos \varphi ,\sin \varphi )}$${\görüntüleme stili P}$${\görüntüleme stili O}$

${\displaystyle x'=\cos \varphi ,\quad y'=\sin \varphi }$

elips için okuyun:

${\displaystyle x'=\operatöradı {cn} (u,m),\quad y'=\operatöradı {sn} (u,m).}$

Yani doğrunun birim çemberle kesiştiği noktanın x ve y eksenleri üzerindeki izdüşümleri basit ve . Bu projeksiyonlar 'trigonometri olarak tanımlama' olarak yorumlanabilir. Kısacası: ${\görüntüleme stili P'}$${\görüntüleme stili OP}$${\görüntüleme stili \operatör adı {cn} (u,m)}$${\displaystyle \operatöradı {sn} (u,m)}$

${\displaystyle \operatöradı {cn} (u,m)={\frac {x}{r(\varphi ,m)}},\quad \operatöradı {sn} (u,m)={\frac {y} {r(\varphi ,m)}},\quad \operatöradı {dn} (u,m)={\frac {1}{r(\varphi ,m)}}.}$

İçin ve noktasının değeri ile ve parametre alırsak alalım, ilişkiyi taktıktan sonra: ${\görüntüleme stili x}$${\görüntüleme stili y}$${\görüntüleme stili P}$${\görüntüleme stili u}$${\görüntüleme stili m}$

${\displaystyle r(\varphi ,m)={\frac {1}{\operatör adı {dn} (u,m)}}}$

içine: bu: ${\displaystyle x=r(\varphi ,m)\cos(\varphi ),y=r(\varphi ,m)\sin(\varphi )}$

${\displaystyle x={\frac {\operatöradı {cn} (u,m)}{\operatöradı {dn} (u,m)}},\quad y={\frac {\operatöradı {sn} (u, m)}{\operatör adı {dn} (u,m)}}.}$

Birim elips üzerindeki noktaların x - ve y - koordinatları için sonraki ilişkiler , birim çember üzerindeki noktaların koordinatları için ilişkilerin genelleştirilmesi olarak düşünülebilir . ${\displaystyle x=\cos \varphi ,y=\sin\varphi }$

Aşağıdaki tablo, ( x , y , r ) ve ( φ ,dn) değişkenlerindeki tüm Jacobi eliptik fonksiyonları pq(u,m) için ifadeleri şu şekilde özetlemektedir:${\displaystyle r={\sqrt {x^{2}+y^{2}}}}$

{x,y,r} ve {φ,dn} fonksiyonları olarak Jacobi eliptik fonksiyonları pq[u,m]

		Q
		C	s	n	NS
P
	C	1	${\displaystyle x/y=\cot(\phi )}$	${\displaystyle x/r=\cos(\phi )}$	${\displaystyle x=\cos(\phi )/\operatöradı {dn} }$
	s	${\displaystyle y/x=\tan(\phi )}$	1	${\displaystyle y/r=\sin(\phi )}$	${\displaystyle y=\sin(\phi )/\operatöradı {dn} }$
	n	${\displaystyle r/x=\sec(\phi )}$	${\görüntüleme stili r/y=\csc(\phi )}$	1	${\displaystyle r=1/\operatör adı {dn} }$
	NS	${\displaystyle 1/x=\operatör adı {dn} \sec(\phi )}$	${\displaystyle 1/y=\operatör adı {dn} \csc(\phi )}$	${\displaystyle 1/r=\operatör adı {dn} }$	1

Jacobi teta fonksiyonları cinsinden tanım

Eşdeğer olarak, Jacobi'nin eliptik fonksiyonları onun teta fonksiyonları cinsinden tanımlanabilir . Biz kısaltmak Eğer olarak ve sırasıyla ( teta sabitleri ) daha sonra teta fonksiyonu eliptik modülü k olduğunu . ayarlarsak , elimizde ${\görüntüleme stili \vartheta (0;\tau )}$${\görüntüleme stili\vartheta }$${\displaystyle \vartheta _{01}(0;\tau ),\vartheta _{10}(0;\tau ),\vartheta _{11}(0;\tau )}$${\displaystyle \vartheta _{01},\vartheta _{10},\vartheta _{11}}$ ${\displaystyle k=\sol({\vartheta _{10} \over\vartheta }\sağ)^{2}}$${\displaystyle u=\pi \vartheta ^{2}z}$

${\displaystyle {\begin{aligned}\operatorname {sn} (u;k)&=-{\vartheta \vartheta _{11}(z;\tau ) \over \vartheta _{10}\vartheta _{01 }(z;\tau )}\\[7pt]\operatöradı {cn} (u;k)&={\vartheta _{01}\vartheta _{10}(z;\tau ) \over \vartheta _{ 10}\vartheta _{01}(z;\tau )}\\[7pt]\operatöradı {dn} (u;k)&={\vartheta _{01}\vartheta (z;\tau ) \over \ vartheta \vartheta _{01}(z;\tau )}\end{hizalı}}}$

Jacobi fonksiyonları eliptik modül cinsinden tanımlandığından , bunu tersine çevirmemiz ve cinsinden bulmamız gerekiyor . Biz başlamak , tamamlayıcı modülü . Bunun bir işlevi olarak ${\görüntüleme stili k(\tau )}$${\görüntüleme stili\tau }$${\görüntüleme stili k}$${\displaystyle k'={\sqrt {1-k^{2}}}}$${\görüntüleme stili\tau }$

${\displaystyle k'(\tau )=\left({\vartheta _{01} \over \vartheta }\sağ)^{2}.}$

önce tanımlayalım

${\displaystyle \ell ={1 \2'den fazla}{1-{\sqrt {k'}} \1'den fazla{\sqrt {k'}}}={1 \2'den fazla}{\vartheta -\vartheta _ {01} \over \vartheta +\vartheta _{01}}.}$

Sonra tanımlamak nome olarak ve genişletmek bir şekilde güç serileri nome de , biz elde ${\displaystyle q=\exp(\pi i\tau )}$${\görüntüleme stili\el }$${\görüntüleme stili q}$

${\displaystyle \ell ={q+q^{9}+q^{25}+\cdots \over 1+2q^{4}+2q^{16}+\cdots }.}$

Serinin geri dönüşü şimdi veriyor

${\displaystyle q=\ell +2\ell ^{5}+15\ell ^{9}+150\ell ^{13}+1707\ell ^{17}+20910\ell ^{21}+268616\ ^{25}+\cdots .}$

'nin sanal kısmının büyük veya eşit olduğu duruma indirgeyebileceğimiz için, mutlak değerinin küçük veya eşit olduğunu varsayabiliriz ; bu kadar küçük değerler için yukarıdaki seriler çok hızlı bir şekilde yakınsar ve bize uygun değeri bulmamızı sağlar . ${\görüntüleme stili\tau }$${\displaystyle {\sqrt {3}}/2}$${\görüntüleme stili q}$${\displaystyle \exp(-\pi {\sqrt {3}}/2)\yaklaşık 0.0658}$${\görüntüleme stili q}$

Neville teta fonksiyonları cinsinden tanım

Jacobi eliptik işlevleri, Neville teta işlevleri kullanılarak çok basit bir şekilde tanımlanabilir :

${\displaystyle \operatöradı {pq} (u,m)={\frac {\theta _{\operatöradı {p} }(u,m)}{\theta _{\operatöradı {q} }(u,m) }}}$

Jacobi eliptik fonksiyonlarının karmaşık ürünlerinin sadeleştirilmesi, genellikle bu özdeşlikler kullanılarak daha kolay hale getirilir.

Jacobi dönüşümleri

Jacobi hayali dönüşümler

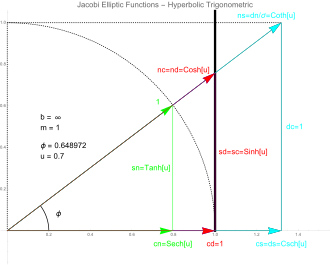
Belirli bir açı φ değeri için dejenere Jacobi eğrisinin (x ² +y ² /b ² =1, b=sonsuz) ve on iki Jacobi Eliptik fonksiyonunun pq(u,1) grafiği. Katı eğri, m=1 ve u=F(φ,1) olan dejenere elipstir (x ² =1), burada F(.,.) birinci türden eliptik integraldir . Noktalı eğri birim çemberdir. . Bunlar m=0 (dairesel trigonometrik fonksiyonlar) için Jacobi fonksiyonları olduğundan, ancak hayali argümanlarla altı hiperbolik trigonometrik fonksiyona karşılık gelirler.

Jacobi sanal dönüşümleri, sanal değişken iu'nun çeşitli fonksiyonlarını veya eşdeğer olarak, m parametresinin çeşitli değerleri arasındaki ilişkileri ilişkilendirir . Başlıca işlevler açısından:

${\displaystyle \operatöradı {cn} (u,m)=\operatöradı {nc} (i\,u,1\!-\!m)}$

${\displaystyle \operatöradı {sn} (u,m)=-i\operatöradı {sc} (i\,u,1\!-\!m)}$

${\displaystyle \operatöradı {dn} (u,m)=\operatöradı {dc} (i\,u,1\!-\!m)}$

Çarpma kuralı kullanılarak, diğer tüm fonksiyonlar yukarıdaki üç terimle ifade edilebilir. Dönüşümler genellikle olarak yazılabilir . Aşağıdaki tablo , belirtilen pq( u,m ) için verir. (Argümanlar bastırılır) ${\displaystyle \operatöradı {pq} (u,m)=\gamma _{\operatöradı {pq} }\operatöradı {pq} '(i\,u,1\!-\!m)}$${\displaystyle \gamma _{\operatöradı {pq} }\operatöradı {pq} '(i\,u,1\!-\!m)}$${\görüntüleme stili (i\,u,1\!-\!m)}$

Jacobi Hayali dönüşümler ${\displaystyle \gamma _{\operatöradı {pq} }\operatöradı {pq} '(i\,u,1\!-\!m)}$

		Q
		C	s	n	NS
P
	C	1	ben ns	nc	nd
	s	-i sn	1	-i sc	-ben sd
	n	cn	ben cs	1	CD
	NS	dn	ben ds	DC	1

Yana hiperbolik trigonometrik fonksiyonlar hayali bağımsız değişken ile, dairesel trigonometrik fonksiyonlar ile orantılıdır, Jacobi fonksiyonları m = 1 için hiperbolik fonksiyonlar ortaya çıkaracaktır izler. Şekilde, Jacobi eğrisi x =1 ve x =-1'de iki dikey çizgiye yozlaşmıştır .

Jacobi gerçek dönüşümleri

Jacobi gerçek dönüşümleri, eliptik fonksiyonlar için m'nin alternatif değerleriyle ifadeler verir . Dönüşümler genellikle olarak yazılabilir . Aşağıdaki tablo , belirtilen pq( u,m ) için verir. (Argümanlar bastırılır) ${\displaystyle \operatöradı {pq} (u,m)=\gamma _{\operatöradı {pq} }\operatöradı {pq} '(k\,u,1/m)}$${\displaystyle \gamma _{\operatöradı {pq} }\operatöradı {pq} '(k\,u,1/m)}$${\görüntüleme stili (k\,u,1/m)}$

Jacobi Real dönüşümleri ${\displaystyle \gamma _{\operatöradı {pq} }\operatöradı {pq} '(k\,u,1/m)}$

		Q
		C	s	n	NS
P
	C	1	${\görüntüleme stili k}$ ds	dn	DC
	s	${\displaystyle {\frac {1}{k}}}$ SD	1	${\displaystyle {\frac {1}{k}}}$ sn	${\displaystyle {\frac {1}{k}}}$ sc
	n	nd	${\görüntüleme stili k}$ ns	1	nc
	NS	CD	${\görüntüleme stili k}$ cs	cn	1

Diğer Jacobi dönüşümleri

Jacobi'nin gerçek ve hayali dönüşümleri, üç basit dönüşüm daha elde etmek için çeşitli şekillerde birleştirilebilir. Gerçek ve hayali dönüşümler, altı dönüşümden oluşan bir grupta ( D ₃ veya Anharmonik grup ) iki dönüşümdür. Eğer

${\displaystyle \mu _{R}(m)=1/m}$

için dönüşümdür m, gerçek transformasyon parametre ve

${\displaystyle \mu _{I}(m)=1-m=m'}$

dönüştürmesidir m sadece üç daha fazla olanak veren daha sonra diğer dönüşümler bu iki temel dönüşümlerin ardışık olarak uygulanması ile inşa edilebilir hayali dönüşüm de:

${\displaystyle {\begin{hizalanmış}\mu _{IR}(m)&=&\mu _{I}(\mu _{R}(m))&=&-m'/m\\\mu _{RI}(m)&=&\mu _{R}(\mu _{I}(m))&=&1/m'\\\mu _{RIR}(m)&=&\mu _ {R}(\mu _{I}(\mu _{R}(m)))&=&-m/m'\end{hizalı}}}$

Bu beş dönüşüm, özdeşlik dönüşümü (μ _U (m)=m) ile birlikte 6 element grubunu verir. Jacobi eliptik fonksiyonları ile ilgili olarak, genel dönüşüm sadece üç fonksiyon kullanılarak ifade edilebilir:

${\displaystyle \operatöradı {cs} (u,m)=\gamma _{i}\operatöradı {cs'} (\gamma _{i}u,\mu _{i}(m))}$

${\displaystyle \operatöradı {ns} (u,m)=\gamma _{i}\operatöradı {ns'} (\gamma _{i}u,\mu _{i}(m))}$

${\displaystyle \operatöradı {ds} (u,m)=\gamma _{i}\operatöradı {ds'} (\gamma _{i}u,\mu _{i}(m))}$

burada i γ dönüşümü, tanımlama, U, I, IR, R, RI, veya rir = _ı bu üç işlevin için bir çarpım faktörü yaygındır ve asal dönüştürülmüş fonksiyonunu gösterir. Diğer dokuz dönüştürülmüş işlev, yukarıdaki üçünden oluşturulabilir. Dönüşümü temsil etmek için cs, ns, ds fonksiyonlarının seçilmesinin nedeni, diğer fonksiyonların bu üçünün oranları (tersi hariç) olması ve çarpma faktörlerinin birbirini götürmesidir.

Aşağıdaki tablo, üç ps işlevi için çarpım faktörlerini, dönüştürülmüş m'leri ve altı dönüşümün her biri için dönüştürülmüş işlev adlarını listeler . (Her zamanki gibi, k ² =m, 1-k ² =k ₁ ² =m' ve argümanlar ( ) gizlenir) ${\displaystyle \gamma _{i}u,\mu _{i}(m)}$

Altı dönüşüm için parametreler

Dönüşüm ben	${\görüntüleme stili \gama _{i}}$	${\görüntüleme stili \mu _{i}(m)}$	cs'	ns'	ds'
sen	1	m	cs	ns	ds
ben	ben	m'	ns	cs	ds
kızılötesi	ik	-a'/m	ds	cs	ns
r	k	1/m	ds	ns	cs
ri	ik 1	1/m'	ns	ds	cs
RIR	k 1	-a/m'	cs	ds	ns

Böylece, örneğin, RIR dönüşümü için aşağıdaki tabloyu oluşturabiliriz. Dönüşüm genellikle yazılır (Argümanlar bastırılır) ${\displaystyle \operatöradı {pq} (u,m)=\gamma _{\operatöradı {pq} }\,\operatöradı {pq'} (k'\,u,-m/m')}$${\görüntüleme stili (k'\,u,-m/m')}$

RIR dönüşümü ${\displaystyle \gamma _{\operatöradı {pq} }\,\operatöradı {pq'} (k'\,u,-m/m')}$

		Q
		C	s	n	NS
P
	C	1	k' cs	CD	cn
	s	${\displaystyle {\frac {1}{k'}}}$ sc	1	${\displaystyle {\frac {1}{k'}}}$ SD	${\displaystyle {\frac {1}{k'}}}$ sn
	n	DC	${\görüntüleme stili k'}$ ds	1	dn
	NS	nc	${\görüntüleme stili k'}$ ns	nd	1

Jacobi dönüşümlerinin değeri, herhangi bir karmaşık değerli parametre m ile herhangi bir Jacobi eliptik fonksiyon kümesinin, 0<= m <=1 olan başka bir kümeye dönüştürülebilmesi ve u'nun gerçek değerleri için , fonksiyon değerlerinin gerçek olacağıdır. .

Jacobi hiperbol

Jacobi hiperbolünün ( x ² + y ² /b ² =1, b sanal) ve on iki Jacobi Eliptik fonksiyonunun pq(u,m) φ açısı ve b parametresinin belirli değerleri için grafiği . Katı eğrisi, hiperbol olan m = 1-1 / b ² ve u = F (φ, m) , F (.,.) Olan eliptik yekpare birinci tür. Noktalı eğri birim çemberdir. ds-dc üçgeni için, σ = sin(φ)cos(φ) .

Karmaşık sayıları tanıtan elipsimizin ilişkili bir hiperbolü vardır:

${\displaystyle x^{2}-{\frac {y^{2}}{b^{2}}}=1}$

Jacobi'nin hayali dönüşümünü x ve  y için yukarıdaki denklemdeki eliptik fonksiyonlara uygulamaktan .

${\displaystyle x={\frac {1}{\operatöradı {dn} (u,1-m)}},\quad y={\frac {\operatöradı {sn} (u,1-m)}{\ operatör adı {dn} (u,1-m)}}}$

koyabileceğimiz sonucu çıkar . Yani elipsimiz, m'nin 1 m ile değiştirildiği bir ikili elipse sahip. Bu, Giriş bölümünde bahsedilen karmaşık halkaya yol açar. Genel olarak, m karmaşık bir sayı olabilir, ancak m gerçek ve m<0 olduğunda eğri, ana ekseni x yönünde olan bir elipstir. m=0'da eğri bir dairedir ve 0<m<1 için eğri, ana ekseni y yönünde olan bir elipstir. m=1'de, eğri x=+/- 1'de iki dikey çizgiye dönüşür. m>1 için eğri bir hiperboldür. m karmaşık ancak gerçek olmadığında, x veya y veya her ikisi de karmaşıktır ve eğri gerçek bir xy diyagramında tanımlanamaz. ${\displaystyle x=\operatöradı {dn} (u,1-m),y=\operatöradı {sn} (u,1-m)}$

küçük fonksiyonlar

İşlev adının iki harfinin sırasını tersine çevirmek, yukarıdaki üç işlevin karşılıklarını verir:

${\displaystyle {\begin{hizalanmış}\operatöradı {ns} (u)={\frac {1}{\operatöradı {sn} (u)}},\qquad \operatöradı {nc} (u)={\frac {1}{\operatöradı {cn} (u)}},\qquad \operatöradı {nd} (u)={\frac {1}{\operatöradı {dn} (u)}}.\end{hizalı}} }$

Benzer şekilde, üç temel fonksiyonun oranları payın ilk harfine ve ardından paydanın ilk harfine karşılık gelir:

${\displaystyle {\begin{hizalanmış}\operatöradı {sc} (u)={\frac {\operatöradı {sn} (u)}{\operatöradı {cn} (u)}},\qquad \operatöradı {sd} (u)={\frac {\operatöradı {sn} (u)}{\operatöradı {dn} (u)}},\qquad \operatöradı {dc} (u)={\frac {\operatöradı {dn} ( u)}{\operatöradı {cn} (u)}},\qquad \operatöradı {ds} (u)={\frac {\operatöradı {dn} (u)}{\operatöradı {sn} (u)}} ,\qquad \operatöradı {cs} (u)={\frac {\operatöradı {cn} (u)}{\operatöradı {sn} (u)}},\qquad \operatöradı {cd} (u)={\ frac {\operatöradı {cn} (u)}{\operatöradı {dn} (u)}}.\end{hizalı}}}$

Daha kompakt, biz var

${\displaystyle \operatöradı {pq} (u)={\frac {\operatöradı {pn} (u)}{\operatöradı {qn} (u)}}}$

burada p ve q, s, c, d harflerinden herhangi biridir.

Periyodiklik, kutuplar ve kalıntılar

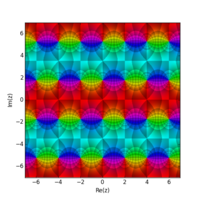
Kutuplar ve sıfırlar ile birlikte bir fonksiyon kompleksi argümanı u olarak on iki Jacobi Eliptik fonksiyonu pq(u,m) için faz çizimleri. Çizimler, gerçek ve hayali yönlerde bir tam döngünün üzerindedir ve renkli kısım sağ alttaki renk çarkına göre fazı gösterir (önemsiz dd işlevinin yerini alır). Genliği 1/3'ün altında olan bölgeler siyah renkle kabaca sıfırın yerini belirtirken, amplitüdü 3'ün üzerinde olan bölgeler beyaz renkle kabaca bir direğin konumunu belirtir. Tüm grafikler m=2/3'ü kullanır ve K=K(m), K'=K(1-m), K(.) birinci türün tam eliptik integralidir. Kutuplardaki oklar sıfır faz yönünü gösterir. Sağ ve sol oklar sırasıyla pozitif ve negatif gerçek kalıntıları ifade eder. Yukarı ve aşağı oklar sırasıyla pozitif ve negatif hayali kalıntıları ifade eder.

u argümanının karmaşık düzleminde , Jacobi eliptik fonksiyonları tekrar eden bir kutuplar (ve sıfırlar) modeli oluşturur. Kutupların kalıntılarının tümü aynı genliğe sahiptir, yalnızca işaret bakımından farklılık gösterir. Her pq(u,m) fonksiyonu, kutupların ve sıfırların konumlarının değiştirildiği bir ters qp(u,m) fonksiyonuna sahiptir. Tekrar periyotları, gerçek ve hayali yönlerde genellikle farklıdır, bu nedenle onları tanımlamak için "çift periyodik" terimi kullanılır.

Jacobi eliptik fonksiyonlarının çift periyodikliği şu şekilde ifade edilebilir:

${\displaystyle \operatöradı {pq} (u+2\alpha K(m)+2i\beta K(1-m)\,,\,m)=(-1)^{\gamma }\operatöradı {pq} (u,m)}$

burada α ve β herhangi bir tam sayı çiftidir. K(.), çeyrek periyot olarak da bilinen birinci türden tam eliptik integraldir . Negatif birliğin gücü (γ) aşağıdaki tabloda verilmiştir:

${\görüntüleme stili \gama }$

		Q
		C	s	n	NS
P
	C	0	β	α+β	α
	s	β	0	α	α+β
	n	α+β	α	0	β
	NS	α	α+β	β	0

(-1) ^γ faktörü -1'e eşit olduğunda, denklem yarı periyodikliği ifade eder. Birliğe eşit olduğunda tam periyodikliği ifade eder. Örneğin, α çift olduğunda sadece α içeren girdiler için tam periyodikliğin yukarıdaki denklemle ifade edildiği ve fonksiyonun 4K(m) ve 2iK(1-m) tam periyotlarına sahip olduğu görülebilir. Benzer şekilde, yalnızca β içeren girişlere sahip fonksiyonlar 2K(m) ve 4iK(1-m)'lik tam periyotlara sahipken, α + β'lı fonksiyonlar 4K(m) ve 4iK(1-m)'lik tam periyotlara sahiptir.

Kutupların ve sıfırların konumuyla birlikte fazı gösteren, her fonksiyon için bir tekrar eden birim çizen sağdaki diyagramda, bir dizi düzenlilik not edilebilir: Her fonksiyonun tersi köşegenin karşısındadır ve aynı boyuta sahiptir. kutuplar ve sıfırlar değiş tokuş edilen birim hücre. (0,0), (K,0), (0,K') ve (K,K') ile oluşturulan yardımcı dikdörtgendeki kutup ve sıfır düzenlemesi, yukarıdaki tanıtım. Ayrıca, kutupları gösteren beyaz ovallerin boyutu, o kutup için tortunun genliğinin kabaca bir ölçüsüdür. Şekildeki (yani yardımcı dikdörtgendeki) orijine en yakın kutupların kalıntıları aşağıdaki tabloda listelenmiştir:

Jacobi Eliptik Fonksiyonların Kalıntıları

		Q
		C	s	n	NS
P
	C		1	${\displaystyle -{\frac {i}{k}}}$	${\displaystyle -{\frac {1}{k}}}$
	s	${\displaystyle -{\frac {1}{k'}}}$		${\displaystyle {\frac {1}{k}}}$	${\displaystyle -{\frac {i}{k\,k'}}}$
	n	${\displaystyle -{\frac {1}{k'}}}$	1		${\displaystyle -{\frac {i}{k'}}}$
	NS	-1	1	${\görüntüleme stili -i}$

Uygulanabilir olduğunda, yukarıda 2K yer değiştiren veya 2K' sağa kaydırılan kutuplar aynı değere sahiptir, ancak işaretleri ters çevrilirken, çapraz olarak zıt olanlar aynı değere sahiptir. Sol ve alt kenarlardaki kutuplar ve sıfırlar, birim hücrenin bir parçası olarak kabul edilirken, üst ve sağ kenarlardakiler değildir.

Fonksiyonların kareleri arasındaki ilişkiler

Fonksiyonların kareleri arasındaki ilişkiler iki temel ilişkiden türetilebilir (Argümanlar ( u , m ) bastırılmış):

${\displaystyle \operatöradı {cn} ^{2}+\operatöradı {sn} ^{2}=1}$

${\displaystyle \operatöradı {cn} ^{2}+m'\operatöradı {sn} ^{2}=\operatöradı {dn} ^{2}}$

burada m + m'  = 1 ve m  =  k ² . nq formunun herhangi bir fonksiyonu ile çarpıldığında daha genel denklemler elde edilir:

${\displaystyle \operatöradı {cq} ^{2}+\operatöradı {sq} ^{2}=\operatöradı {nq} ^{2}}$

${\displaystyle \operatöradı {cq} ^{2}+m'\operatöradı {sq} ^{2}=\operatöradı {dq} ^{2}}$

İle q = d , birim çember için denklemlere trigonometrik bu karşılık gelir ( ) ve birim elipsin ( ile), X = cd , y SD = ve r = nd . Çarpma kuralı kullanılarak başka ilişkiler türetilebilir. Örneğin: ${\displaystyle x^{2}+y^{2}=r^{2}}$${\displaystyle x^{2}+ay^{2}=1}$

${\displaystyle -\operatöradı {dn} ^{2}+m'=-m\operatöradı {cn} ^{2}=m\operatöradı {sn} ^{2}-m}$

${\displaystyle -m'\operatöradı {nd} ^{2}+m'=-mm'\operatöradı {sd} ^{2}=m\operatöradı {cd} ^{2}-m}$

${\displaystyle m'\operatöradı {sc} ^{2}+m'=m'\operatöradı {nc} ^{2}=\operatöradı {dc} ^{2}-m}$

${\displaystyle \operatöradı {cs} ^{2}+m'=\operatöradı {ds} ^{2}=\operatöradı {ns} ^{2}-m}$

Toplama teoremleri

Fonksiyonlar iki kare ilişkisini sağlar

${\displaystyle \operatöradı {cn} ^{2}(u,k)+\operatöradı {sn} ^{2}(u,k)=1,\,}$

${\displaystyle \operatöradı {dn} ^{2}(u,k)+k^{2}\operatöradı {sn} ^{2}(u,k)=1.\,}$

Buradan, (cn, sn, dn) 'nin , yukarıdaki iki denklem tarafından tanımlanan iki kuadranın kesişimi olan bir eliptik eğriyi parametrelendirdiğini görüyoruz . Şimdi Jacobi fonksiyonları için toplama formülleri ile bu eğri üzerindeki noktalar için bir grup kanunu tanımlayabiliriz.

${\displaystyle {\begin{hizalanmış}\operatöradı {cn} (x+y)&={\operatöradı {cn} (x)\operatöradı {cn} (y)-\operatöradı {sn} (x)\operatöradı { sn} (y)\operatöradı {dn} (x)\operatöradı {dn} (y) \over {1-k^{2}\operatöradı {sn} ^{2}(x)\operatöradı {sn} ^{ 2}(y)}},\\[8pt]\operatöradı {sn} (x+y)&={\operatöradı {sn} (x)\operatöradı {cn} (y)\operatöradı {dn} (y) +\operatöradı {sn} (y)\operatöradı {cn} (x)\operatöradı {dn} (x) \over {1-k^{2}\operatöradı {sn} ^{2}(x)\operatöradı { sn} ^{2}(y)}},\\[8pt]\operatöradı {dn} (x+y)&={\operatöradı {dn} (x)\operatöradı {dn} (y)-k^{ 2}\operatöradı {sn} (x)\operatöradı {sn} (y)\operatöradı {cn} (x)\operatöradı {cn} (y) \over {1-k^{2}\operatöradı {sn} ^ {2}(x)\operatöradı {sn} ^{2}(y)}}.\end{hizalı}}}$

Çift açılı formüller, x = y ayarlanarak yukarıdaki denklemlerden kolayca türetilebilir . Yarım açı formülleri şu şekildedir:

${\displaystyle \operatöradı {pq} ({\tfrac {1}{2}}u,m)^{2}=f_{\mathrm {p} }/f_{\mathrm {q} }}$

nerede:

${\displaystyle f_{\mathrm {c} }=\operatöradı {cn} (u,m)+\operatöradı {dn} (u,m)}$

${\displaystyle f_{\mathrm {s} }=1-\operatöradı {cn} (u,m)}$

${\displaystyle f_{\mathrm {n} }=1+\operatör adı {dn} (u,m)}$

${\displaystyle f_{\mathrm {d} }=(1+\operatöradı {dn} (u,m))-m(1-\operatöradı {cn} (u,m))}$

Özel değerler

K'nin yarılanması için değerler:

${\displaystyle \operatöradı {sn} \left[{\tfrac {1}{2}}K(k);k\sağ]={\frac {1}{\sqrt {1+{\sqrt {1-k ^{2}}}}}}}$ve ve${\displaystyle \operatöradı {cn} \left[{\tfrac {1}{2}}K(k);k\sağ]={\frac {\sqrt[{4}]{1-k^{2} }}{\sqrt {1+{\sqrt {1-k^{2}}}}}}}$${\displaystyle \operatöradı {dn} \sol[{\tfrac {1}{2}}K(k);k\sağ]={\sqrt[{4}]{1-k^{2}}}}$

K'nin üçte biri için değerler:

${\displaystyle \operatöradı {sn} \left[{\frac {1}{3}}K\left({\frac {x^{3}}{{\sqrt {x^{6}+1}}+) 1}}\right);{\frac {x^{3}}{{\sqrt {x^{6}+1}}+1}}\right]={\frac {{\sqrt {2{\ sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}-1}{{\sqrt {2 {\sqrt {x^{4}-x^{2}+1}}-x^{2}+2}}+{\sqrt {x^{2}+1}}+1}}}$

x^3'ü elde etmek için modülün arktanjantının iki katının tanjantını almanız gerekir.

Ayrıca bu denklem, K'nin üçüncüsünün sn-değerine yol açar:

${\displaystyle k^{2}s^{4}-2k^{2}s^{3}+2s-1=0}$

${\displaystyle s=\operatöradı {sn} \sol[{\tfrac {1}{3}}K(k);k\sağ]}$

Bu denklemler Jacobi-Fonksiyonlarının diğer değerlerine yol açar:

${\displaystyle \operatöradı {cn} \sol[{\tfrac {2}{3}}K(k);k\sağ]=1-\operatöradı {sn} \left[{\tfrac {1}{3} }K(k);k\sağ]}$

${\displaystyle \operatöradı {dn} \sol[{\tfrac {2}{3}}K(k);k\sağ]=1/\operatöradı {sn} \left[{\tfrac {1}{3} }K(k);k\sağ]-1}$

K'nin beşte biri için değerler:

Aşağıdaki denklem aşağıdaki çözüme sahiptir:

${\displaystyle 4k^{2}x^{6}+8k^{2}x^{5}+2(1-k^{2})^{2}x-(1-k^{2}) ^{2}=0}$

${\displaystyle x={\frac {1}{2}}-{\frac {1}{2}}k^{2}\operatorname {sn} \left[{\tfrac {2}{5}}K (k);k\sağ]^{2}\operatöradı {sn} \left[{\tfrac {4}{5}}K(k);k\sağ]^{2}={\frac {\operatöradı {sn} \left[{\frac {4}{5}}K(k);k\sağ]^{2}-\operatorname {sn} \left[{\frac {2}{5}}K( k);k\sağ]^{2}}{2\operatöradı {sn} \left[{\frac {2}{5}}K(k);k\sağ]\operatöradı {sn} \left[{ \frac {4}{5}}K(k);k\sağ]}}}$

sn değerlerini elde etmek için x çözümünü aşağıdaki ifadelere koymalısınız:

${\displaystyle {\sqrt {k^{2}+1}}\operatöradı {sn} \left[{\tfrac {2}{5}}K(k);k\sağ]={\sqrt {2( -x^{2}-x+1)(x^{2}+1-x{\sqrt {x^{2}+1}})}}}$

${\displaystyle {\sqrt {k^{2}+1}}\operatöradı {sn} \left[{\tfrac {4}{5}}K(k);k\sağ]={\sqrt {2( -x^{2}-x+1)(x^{2}+1+x{\sqrt {x^{2}+1}})}}}$

Nome açısından genişleme

Let nome olmak , , ve let . Daha sonra fonksiyonların Lambert serisi gibi açılımları vardır.${\displaystyle q=\exp(-\pi K'(k)/K(k))=e^{i\pi \tau }}$${\displaystyle \operatöradı {Im} (\tau )>0}$${\görüntüleme stili m=k^{2}}$${\görüntüleme stili v=\pi u/(2K(k))}$

${\displaystyle \operatöradı {sn} (u;k)={\frac {2\pi }{kK(k)}}\sum _{n=0}^{\infty }{\frac {q^{n +1/2}}{1-q^{2n+1}}}\sin((2n+1)v),}$

${\displaystyle \operatöradı {cn} (u;k)={\frac {2\pi }{kK(k)}}\sum _{n=0}^{\infty }{\frac {q^{n +1/2}}{1+q^{2n+1}}}\cos((2n+1)v),}$

${\displaystyle \operatöradı {dn} (u;k)={\frac {\pi }{2K(k)}}+{\frac {2\pi }{K(k)}}\sum _{n= 1}^{\infty }{\frac {q^{n}}{1+q^{2n}}}\cos(2nv)}$

ne zaman . ${\displaystyle q\exp(2|\operatöradı {Im} (v)|)<1}$

Doğrusal olmayan adi diferansiyel denklemlerin çözümleri olarak Jacobi eliptik fonksiyonları

Türevleri, üç temel Jacobi eliptik fonksiyonları şunlardır:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatöradı {sn} (z)=\operatöradı {cn} (z)\operatöradı {dn} (z),}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatöradı {cn} (z)=-\operatöradı {sn} (z)\operatöradı {dn} (z),}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatöradı {dn} (z)=-k^{2}\operatöradı {sn} (z)\operatöradı {cn} (z).}$

Bunlar, aşağıdaki tabloda gösterildiği gibi diğer tüm fonksiyonların türevlerini türetmek için kullanılabilir (argümanlar (u,m) bastırılmıştır):

türevler ${\displaystyle {\frac {d}{du}}\operatöradı {pq} (u,m)}$

		Q
		C	s	n	NS
P
	C	0	-ds ns	-dn sn	-m' ve sd
	s	dc nc	0	cn dn	cd nd
	n	DC sc	-cs ds	0	m cd sd
	NS	m' nc sc	-cs ns	-m cn sn	0

İle teoremler yukarıdaki ek ve için belirli k 0 <  k  <1 majör işlevleri dolayısıyla aşağıdaki doğrusal olmayan çözümleri bulunmaktadır sıradan diferansiyel denklemler :

• ${\displaystyle \operatöradı {sn} (x)}$diferansiyel denklemleri çözer ve${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1+k^{2})y-2k^{2}y^ {3}=0}$${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\sağ)^{2}=(1-y^{2})(1-k^{2 }y^{2})}$
• ${\ Displaystyle \ operatör adı {cn} (x)}$diferansiyel denklemleri çözer ve${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1-2k^{2})y+2k^{2}y^ {3}=0}$${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\sağ)^{2}=(1-y^{2})(1-k^{2 }+k^{2}y^{2})}$
• ${\displaystyle \operatör adı {dn} (x)}$diferansiyel denklemleri çözer ve${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}-(2-k^{2})y+2y^{3}=0 }$${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\sağ)^{2}=(y^{2}-1)(1-k^{2 }-y^{2})}$

Hiperbolik fonksiyonlar açısından yaklaşıklık

Jacobi eliptik fonksiyonları hiperbolik fonksiyonlar cinsinden genişletilebilir. Birliğe yakın olduğunda, öyle ki ve daha yüksek güçler ihmal edilebilir, elimizde: ${\görüntüleme stili m}$${\ Displaystyle m'^{2}}$${\görüntüleme stili m'}$

• sn( u ):
  $${\displaystyle \operatöradı {sn} (u,m)\yaklaşık \tanh(u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u)\operatöradı { sec} ^{2}(u).}$$

  
• cn( u ):
  $${\displaystyle \operatöradı {cn} (u,m)\yaklaşık \operatöradı {sech} (u)-{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u) \tanh(u)\operatöradı {sech} (u).}$$

  
• dn( u ):
  $${\displaystyle \operatöradı {dn} (u,m)\yaklaşık \operatöradı {sech} (u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)+u) \tanh(u)\operatöradı {sech} (u).}$$

  
• ben( sen ):
  $${\displaystyle \operatöradı {am} (u,m)\yaklaşık \operatöradı {gd} (u)+{\frac {1}{4}}m'(\sinh(u)\cosh(u)-u) \operatöradı {sech} (u).}$$

  

Devam eden kesirler

Gerçek sayılar varsayarsak ile ve nome , ile eliptik modülü . Eğer , burada bir birinci türden tam eliptik ayrılmaz , aşağıdaki tutan devam fraksiyonu genişleme${\görüntüleme stili a,p}$${\görüntüleme stili 0<a<p}$ ${\displaystyle q=e^{\pi i\tau }}$${\displaystyle \operatöradı {Im} (\tau )>0}$ ${\textstyle k(\tau )={\sqrt {1-k'(\tau )^{2}}}=(\vartheta _{10}(0;\tau )/\vartheta _{00}(0 ;\tau ))^{2}}$${\displaystyle K[\tau ]=K(k(\tau ))}$${\displaystyle K(x)=\pi /2\cdot {}_{2}F_{1}(1/2,1/2;1;x^{2})}$