Dihedral grup 6 düzen - Dihedral group of order 6

Bir üçgenin permütasyonlu Cayley grafiği

3 elementin permütasyon matrislerini içeren döngü grafiği
( a ve b üreteçleri , yukarıda gösterilen Cayley grafiğindeki ile aynıdır.)

Permütasyon matrislerinin çarpım tablosu olarak Cayley tablosu

Cayley tablosundaki altı elemanın konumları
Sadece nötr elemanlar ana köşegene simetriktir, bu nedenle bu grup değişmeli değildir .

Cayley tablosu genel (ve özel ) lineer grup GL (2, 2) olarak

Gelen matematik , D ₃ (bazen seçenek olarak gösterilen D ₆ ) olan iki düzlemli grup , diğer bir deyişle, derece 3 veya dihedral grubu düzenine Bu izomorf 6. simetrik grubunun S ₃ derece 3. Ayrıca bir olası en küçük değişmeli olmayan grup .

Bu sayfa, bu grubu örnek olarak kullanan birçok grup kavramını göstermektedir.

Simetri grupları

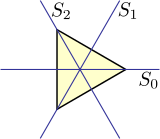
Dihedral D grubu ₃ bir simetri grubu , bir ait eşkenar üçgen sabit bu üçgenin şekli ve pozisyonu terk bu yansıma, döndürme ve bunların kombinasyonları gibi tüm dönüşümler, grubu, yani,. D ₃ durumunda , üçgenin köşelerinin her olası permütasyonu böyle bir dönüşümü oluşturur, böylece bu simetrilerin grubu , üç farklı elementin tüm permütasyonlarının simetrik grubu S _3'e izomorfiktir . Bu, yüksek mertebeden dihedral gruplar için geçerli değildir.

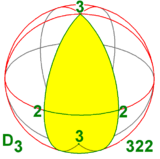
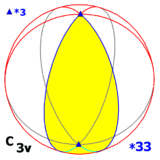
Dihedral grup D ₃ , üç boyutta diğer iki simetri grubuna izomorfiktir:

biri 3 katlı dönüş eksenli ve 2 dikey dikey dönüş eksenli (dolayısıyla bunlardan üçü): D ₃
biri bir yansıma düzleminde (ve dolayısıyla diğer iki yansıma düzleminde) 3-kat dönüş eksenli: C _3v

Üç nesneden oluşan bir kümenin permütasyonları

Başlangıçta RGB sırasına göre yerleştirilmiş üç renkli bloğu (kırmızı, yeşil ve mavi) düşünün. Simetrik grup S ₃ ile bütün olası grubudur yeniden düzenlemeleri , bu blokların. Biz tarafından ifade ederse bir eylem "İlk iki blok takas" ve tarafından b eylem "takas son iki blok", bu iki eylem açısından mümkün olan tüm permütasyon yazabilir.

Çarpımsal biçimde, geleneksel olarak "önce y yap , sonra x yap " eylemi için xy yazarız ; böylece ab , RGB ↦ RBG ↦ BRG eylemidir , yani "son bloğu al ve öne taşı". Biz yazarsanız e (kimlik eylem) "oldukları gibi bloklar bırakın" için, o zaman altı yazabilir permütasyon ait kümesi aşağıdaki eylemlerden olarak üç bloktan:

e : RGB ↦ RGB veya ()
a : RGB ↦ GRB veya (RG)
b : RGB ↦ RBG veya (GB)
ab : RGB ↦ BRG veya (RBG)
ba : RGB ↦ GBR veya (RGB)
aba : RGB ↦ BGR veya (RB)

Parantez içindeki gösterim , döngü gösterimidir .

Aa eyleminin , blokları olduğu gibi bırakarak RGB ↦ GRB ↦ RGB etkisine sahip olduğuna dikkat edin ; böylece aa = e yazabiliriz . Benzer şekilde,

bb = e ,
( aba ) ( aba ) = e ve
( ab ) ( ba ) = ( ba ) ( ab ) = e ;

bu nedenle yukarıdaki eylemlerin her birinin bir tersi vardır.

İnceleme yoluyla, aynı zamanda ilişkilendirilebilirliği ve kapanışı da belirleyebiliriz (gerekli grup aksiyomlarından ikisi ); örneğin not edin

( ab ) a = a ( ba ) = aba ve
( ba ) b = b ( ab ) = bab .

Grup değişmeli değildir, çünkü örneğin ab ≠ ba . Temel a ve b eylemlerinden oluşturulduğu için, onu { a , b } kümesinin oluşturduğunu söylüyoruz .

Grubun sunumu var

{\ displaystyle \ langle r, a \ orta r ^ {3} = 1, a ^ {2} = 1, ara = r ^ {- 1} \ rangle}

ayrıca yazılmış

{\ displaystyle \ langle r, a \ orta r ^ {3}, a ^ {2}, arar \ rangle}

veya

{\ displaystyle \ langle a, b \ mid a ^ {2} = b ^ {2} = (ab) ^ {3} = 1 \ rangle}

ayrıca yazılmış

{\ displaystyle \ langle a, b \ mid a ^ {2}, b ^ {2}, (ab) ^ {3} \ rangle}

burada a ve b takas ve r = ab döngüsel bir permütasyondur. İkinci sunumun, grubun bir Coxeter grubu olduğu anlamına geldiğini unutmayın . (Aslında, tüm dihedral ve simetri grupları Coxeter gruplarıdır.)

Grup işlemlerinin özeti

Jeneratörler ile bir ve b , ek kestirme tanımlamak c =: aba , d : = ab ve f =: ba böylece, a, b, c, d, e ve f , bu grubun elemanlarıdır. Daha sonra grup işlemlerini bir Cayley tablosu şeklinde özetleyebiliriz :

*	e	a	b	c	d	f
e	e	a	b	c	d	f
a	a	e	d	f	b	c
b	b	f	e	d	c	a
c	c	d	f	e	a	b
d	d	c	a	b	f	e
f	f	b	c	a	e	d

Eşit olmayan özdeş olmayan öğelerin yalnızca birbirlerinin tersi olmaları durumunda işe gidip geldiklerini unutmayın. Dolayısıyla grup merkezsizdir , yani grubun merkezi sadece kimlik unsurundan oluşur.

Eşlenik sınıfları

Üç bloğun üç tür permütasyonunu , grubun eşlenik sınıflarını kolayca ayırt edebiliriz :

değişiklik yok (), 1. dereceden bir grup öğesi
iki bloğun değiş tokuşu: (RG), (RB), (GB), 2. dereceden üç grup elemanı
üç bloğun hepsinin döngüsel permütasyonu: (RGB), (RBG), 3. dereceden iki grup elemanı

Örneğin, (RG) ve (RB) 'nin her ikisi de ( x y ) biçimindedir ; R, G ve B harflerinin bir permütasyonu (yani (GB)) notasyonu (RG) (RB) olarak değiştirir. Bu nedenle, (GB), ardından (RB) ve ardından (GB) 'nin tersini uygularsak, ki bu da (GB), sonuçta elde edilen permütasyon (RG) olur.

Eşlenik grup elemanlarının her zaman aynı sıraya sahip olduğuna , ancak genel olarak aynı sıraya sahip iki grup elemanının eşlenik olmasına gerek olmadığına dikkat edin.

Alt gruplar

Kaynaktan Lagrange teoremi herhangi önemsiz olmayan biliyoruz alt grup 6 elemanlı bir grubunun dizi 2 ya da aslında 3. İki olmalıdır siklik permütasyon , kimliği ile üç blok sırasına 3, bir alt grup oluştururlar endeksi 2 ve Her biri kimliğe sahip iki bloğun takasları, sıra 2, indeks 3'ün üç alt grubunu oluşturur. 2. ve 3. dereceden alt grupların varlığı da Cauchy teoreminin bir sonucudur .

İlk bahsedilen olan {(), (RGB) (RBG)}, alternatif grup bir ₃ .

Sol Kosetler ve A sağ Kosetler ₃ denk (bunlar indeks 2 herhangi bir alt grup için olduğu gibi) ve A oluşur ₃ üç swap grubu {(RB) (RG), (BG) }.

{(), (RG)} ' nin sol kosetleri :

{(), (RG)}
{(RB), (RGB)}
{(GB), (RBG)}

{(RG), ()} için doğru kosetler :

{(RG), ()}
{(RBG), (RB)}
{(RGB), (GB)}

Bu nedenle bir ₃ olan , normal ve diğer üç önemsiz olmayan alt gruplar değildir. Bölüm grubu G / A ₃ ile izomorfik C ₂ .

${\ displaystyle G = \ mathrm {A} _ {3} \ rtimes H}$ , H'nin iki öğenin bir alt grubu olduğu yarı yönlü bir çarpım : () ve üç takastan biri. Bu ayrışma aynı zamanda Schur-Zassenhaus teoreminin bir sonucudur (özel durum) .

Permütasyonlar açısından, G / A _3'ün iki grup elemanı , çift permütasyonlar ve tek permütasyonlar kümesidir.

Orijinal grup, bir düzlemin bir nokta etrafında 120 ° dönüşü ve bu noktadan geçen bir çizgiye göre yansıması ile oluşturulmuşsa, bölüm grubu alt kümeler olarak tanımlanabilen iki öğeye sahiptir "sadece döndürün ( veya hiçbir şey yapmayın) "ve" bir ayna görüntüsü alın ".

Bir simetri grubu için olanla Not kare , köşe düzensiz bir permütasyon etmez olmayan bir ayna görüntüsü almak için karşılık gelen, ama bu operasyon için izin dikdörtgenler , yani 90 ° 'lik döndürme ve yansıma diyagonal ekseni uygulanması.

Semidirect ürünleri

${\ displaystyle \ mathrm {C} _ {3} \ rtimes _ {\ varphi} \ mathrm {C} _ {2}}$ olup her ikisi de eğer φ (0) ve φ (1) kimlik vardır. Eğer φ (0) özdeşlik ise ve φ (1), elemanları tersine çeviren C _3'ün önemsiz olmayan otomorfizmiyse, yarı yönlü çarpım, 6 dereceli dihedral grubuna izomorfiktir . ${\ displaystyle \ mathrm {C} _ {3} \ times \ mathrm {C} _ {2}}$

Böylece elde ederiz:

( n ₁ , 0) * ( n ₂ , h ₂ ) = ( n ₁ + n ₂ , h ₂ )

( n ₁ , 1) * ( n ₂ , h ₂ ) = ( n ₁ - n ₂ , 1 + h ₂ )

tüm n ₁ , n, ₂ , C ₃ ve h ₂ C ₂ . Daha kısaca,

{\ displaystyle (n_ {1}, h_ {1}) * (n_ {2}, h_ {2}) = (n_ {1} + (- 1) ^ {h_ {1}} n_ {2}, h_ {1} + h_ {2})}

tüm n ₁ , n, ₂ , C ₃ ve h ₁ , h ₂ C ₂ .

Cayley tablosunda:

	00	10	20	01	11	21
00	00	10	20	01	11	21
10	10	20	00	11	21	01
20	20	00	10	21	01	11
01	01	21	11	00	20	10
11	11	01	21	10	00	20
21	21	11	01	20	10	00

İkinci basamak için aslında bu 4 hücrenin her biri için 3 × 3 eşit değerlere sahip 2 × 2 bir tablomuz olduğunu unutmayın. İlk hane için tablonun sol yarısı sağ tarafla aynıdır, ancak üst yarısı alt yarıdan farklıdır.

İçin direkt bir ürün tablosu Tablo alt yarısının birinci basamak üst yarısında aynıdır dışında aynıdır.

Grup eylemi

Düşünün D ₃ bir şekilde, geometrik bir şekilde simetri grubunun bir izometrileri düzlemi ve karşılık gelen dikkate grubu işlem yansımanın eksenlerinden biri 0 ile 29 0 ila sayılı bir daire 30 eşit aralıklı noktalarda bir dizi.

Bu bölüm, bu vaka için grup eylemi kavramlarını göstermektedir.

Aksiyonu G ile X olarak adlandırılan

geçişli bir iki eğer x , y olarak X bir vardır g olarak G , öyle ki g · x = y ; olay bu değil
sadık (ya da etkin bir, iki farklı için ise) g , h içinde G bir vardır X içinde X, öyle ki g · X ≠ H · X ; durum böyledir, çünkü simetri grupları kimlik dışında "hiçbir şey yapmayan" öğeler içermez.
serbest bir, iki farklı için eğer g , h içinde G ve x de , X Elimizdeki g · X ≠ h · X ; durum böyle değil çünkü yansımalar var

Yörüngeler ve stabilizatörler

D3'ün grup hareketi altında bir daire üzerinde eşit aralıklı 30 noktanın yörüngeleri

Yörünge bir noktası , x in X elemanlarının setidir X olduğu X elemanları tarafından hareket ettirilebilir G . X'in yörüngesi Gx ile gösterilir :

{\ displaystyle Gx = \ sol \ {g \ cdot x \ orta g \ G \ sağ \}}

Yörüngeler {0, 10, 20}, {1, 9, 11, 19, 21, 29}, {2, 8, 12, 18, 22, 28}, {3, 7, 13, 17, 23, 27}, {4, 6, 14, 16, 24, 26} ve {5, 15, 25}. Bir yörünge içindeki noktalar "eşdeğerdir". Bir desen için bir simetri grubu geçerliyse, her yörüngede renk aynıdır.

G'nin eylemi altındaki X'in tüm yörüngelerinin kümesi X / G olarak yazılır .

Eğer Y, a, alt küme ve X , biz bilgileri GY kümesi için { g · y : y ∈ Y ve g ∈ G }. Bu alt küme çağrı Y G altında değişmeyen halinde GY = Y, (eşdeğerdir GY ⊆ Y ) . Bu durumda, G ayrıca Y üzerinde de çalışır . Alt kümesi , Y olarak adlandırılan G altında sabit ise gr · y = Y tüm g olarak G ve y de Y . Örneğin iki yörüngenin birleşimi G altında değişmez , ancak sabit değildir.

Her için x de , X , tanımladığımızı stabilize edici alt grup arasında X (ayrıca izotropi grubu ya da çok az bir grup tüm öğeleri kümesinin gibi) G düzeltme bu x :

{\ displaystyle G_ {x} = \ {g \ in G \ mid g \ cdot x = x \}}

Eğer X bir yansıma noktası (0, 5, 10, 15, 20, veya 25) , kendi dengeleyici kimliğini ve yansıma içeren amacıyla iki grubudur , x . Diğer durumlarda dengeleyici önemsiz gruptur.

Sabit için x de , X , haritayı dikkate G için X tarafından verilen g ↦ g · x . Görüntü bu haritanın yörüngesi olan x ve coimage tüm sol kümesidir kalan sınıfları arasında G _x . Küme teorisinin standart bölüm teoremi daha sonra G / G _x ve Gx arasında doğal bir eşleme verir . Spesifik olarak, eşleştirme hG _x ↦ h · x ile verilir . Bu sonuç yörünge sabitleyici teoremi olarak bilinir . İki küçük yörünge durumunda, dengeleyici önemsiz değildir.

İki eleman ise X ve Y daha sonra aynı yörüngesine aittir, kendi dengeleyici alt gruplar, G, _x ve G _y vardır izomorfik . Daha doğrusu: y = g · x ise G _y = gG _x g ⁻¹ . Örnekte bu, örneğin 5 ve 25, her iki yansıma noktası için geçerlidir. Yaklaşık 25'lik bir yansıma, 10'luk bir dönüşe, yaklaşık 5'lik bir yansımaya ve -10'luk bir dönüşe karşılık gelir.

Yörünge sabitleyici teoremiyle yakından ilgili bir sonuç Burnside'ın lemmasıdır :

{\ displaystyle \ sol | X / G \ sağ | = {\ frac {1} {\ sol | G \ sağ |}} \ toplamı _ {g \ G} \ sol | X ^ {g} \ sağ |}

burada X, ^g ile sabit nokta kümesidir g . Yani yörünge sayısı, grup elemanı başına sabitlenen ortalama nokta sayısına eşittir.

Kimlik için 30 noktanın tümü sabittir, iki dönüş için hiçbiri ve üç yansıma için ikişer: {0, 15}, {5, 20} ve {10, 25}. Böylece, ortalama altı, yörünge sayısı.

Temsil teorisi

İzomorfizme kadar, bu grup, (önemsiz temsil) olarak adlandıracağımız ve alt simgenin boyutu belirttiği üç indirgenemez karmaşık üniter gösterime sahiptir . Üç elemanlı küme üzerinde bir permütasyon grubu olarak tanımlanmasıyla, grup, temel temsil olan vektörün girişlerine izin vererek üzerinde bir temsile sahiptir . Doğrudan bir toplamı olarak parçalanır gibi bu temsil, indirgenemez değildir ve . formun vektörlerin bölme odası olarak görünür ve formun vektörlerdir ortogonal tamamlayıcı hakkında temsilidir . Önemsiz tek boyutlu temsil , grupların derecelendirilmesiyle ortaya çıkar : Eylem, grup elemanının permütasyonunun işaretiyle çarpma işlemidir. Her sonlu grup, düzenli eylemi ile bir döngüsel grubun bir alt grubu olduğu için böyle bir temsile sahiptir. Temsillerin kare boyutlarını ( , grubun sırasını) saydığımızda, bunların hepsinin indirgenemez temsiller olması gerektiğini görüyoruz. ${\ displaystyle I}$ ${\ displaystyle \ rho _ {1}}$ ${\ displaystyle \ rho _ {2}}$ ${\ displaystyle \ mathbb {C} ^ {3}}$ ${\ displaystyle I}$ ${\ displaystyle \ rho _ {2}}$ ${\ displaystyle I}$ ${\ displaystyle (\ lambda, \ lambda, \ lambda), \ lambda \ in \ mathbb {C}}$ ${\ displaystyle \ rho _ {2}}$ ${\ displaystyle (\ lambda _ {1}, \ lambda _ {2}, - \ lambda _ {1} - \ lambda _ {2})}$ ${\ displaystyle \ rho _ {1}}$ ${\ displaystyle \ mathbb {Z} _ {2}}$ ${\ displaystyle 1 ^ {2} + 1 ^ {2} + 2 ^ {2} = 6}$

2 boyutlu indirgenemez doğrusal temsil , eliptik dönüşümler olarak 1 boyutlu bir projektif temsil (yani, projektif çizgide bir eylem , Möbius grubu PGL (2, C ) içine yerleştirme ) verir . Bu , harmonik olmayan grup olarak bilinen 0 ve ± 1 girişli (burada kesirli doğrusal dönüşümler olarak yazılmıştır) matrislerle temsil edilebilir :

sipariş 1: ${\ displaystyle z}$
2. sıra: ${\ displaystyle 1-z, 1 / z, z / (z-1)}$
sipariş 3: ${\ displaystyle (z-1) / z, 1 / (1-z)}$

ve böylece herhangi bir alanın üzerinde bir temsile iner, ki bu her zaman sadıktır / enjekte eder (çünkü iki terim yalnızca bir işaretle farklılık gösterdiği için). İki elemanın ile alan üzerinde yansıtmalı hattı 3 puan vardır ve bu, böylece bir istisnai izomorfizm karakteristik 3'te, bu gömme noktası stabilize çünkü bu noktalar belirgin ve sırası vardır ve yörünge olan 3'den karakteristik Greater ( harmonik çapraz oranı ). Üç elemanlı alan üzerinde, projektif çizginin 4 elemanı vardır ve PGL (2, 3) , 4 eleman S ₄ üzerindeki simetrik gruba izomorfik olduğundan , sonuçta ortaya çıkan gömme , noktanın dengeleyicisine eşittir . ${\ displaystyle S_ {3} \ yaklaşık \ mathrm {PGL} (2,2).}$ ${\ displaystyle -1 = [- 1: 1],}$ ${\ displaystyle 2 = 1/2 = -1}$ ${\ displaystyle \ mathrm {S} _ {3} \ hookrightarrow \ mathrm {S} _ {4}}$ ${\ displaystyle -1}$