Ortalamaya doğru regresyon - Regression toward the mean

Galton'un deneysel kurulumu (Şekil 8)

Olarak istatistik , ortalama doğru regresyon (aynı zamanda ortalama regresyon , ortalamaya reversiyon ve vasat için reversiyon ), eğer a ortaya olgudur örnek noktası a rastgele değişkenin bir uç (yaklaşık bir uç değer ), bu durumda a gelecekteki noktanın ortalamaya veya ortalamaya daha yakın olması muhtemeldir . Yanlış çıkarımlar yapmaktan kaçınmak için , bilimsel deneyler tasarlarken ve verileri yorumlarken ortalamaya doğru regresyon dikkate alınmalıdır.

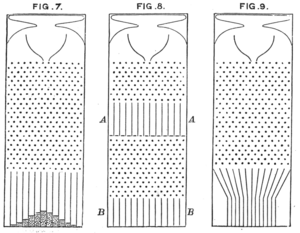
Ortalamaya doğru gerilemenin meydana geldiği koşullar, terimin matematiksel olarak tanımlanma şekline bağlıdır. İngiliz bilge Sir Francis Galton , fenomeni ilk olarak veri noktalarının basit doğrusal regresyonu bağlamında gözlemledi . Galton şu modeli geliştirdi: peletler, doğrudan giriş noktalarının altında ortalanmış normal bir dağılım oluşturmak için bir beş katın içinden düşer . Bu topaklar daha sonra ikinci bir ölçüme karşılık gelen ikinci bir galeriye bırakılabilir. Galton daha sonra ters soruyu sordu: "Bu topaklar nereden geldi?"

Cevap ' ortalama olarak doğrudan üzerinde ' değildi . Bunun yerine, ' ortalama olarak, daha çok ortaya doğru ' idi , basit bir nedenden dolayı, onun üzerinde ortaya doğru, sola doğru, içe doğru dolaşabilecek sol uçta olduğundan daha fazla topak vardı.

Daha az kısıtlayıcı bir yaklaşım olarak, aynı marjinal dağılımlara sahip herhangi bir iki değişkenli dağılım için ortalamaya doğru regresyon tanımlanabilir . Bu tür iki tanım mevcuttur. Bir tanım, "ortalamaya doğru gerileme" teriminin yaygın kullanımıyla yakından uyumludur. Bu tür iki değişkenli dağılımların tümü, bu tanım kapsamında ortalamaya doğru gerileme göstermez. Bununla birlikte, tüm bu tür iki değişkenli dağılımlar, diğer tanım altındaki ortalamaya doğru gerileme göstermektedir.

Jeremy Siegel , "ortalama dönüş" terimini, " getirilerin kısa vadede çok istikrarsız, ancak uzun vadede çok istikrarlı olabileceği " bir finansal zaman serisini tanımlamak için kullanır . Daha niceliksel olarak, ortalama yıllık getirilerin standart sapmasının , elde tutma süresinin tersinden daha hızlı düştüğü, sürecin rastgele bir yürüyüş olmadığı , ancak daha düşük getiri dönemlerini sistematik olarak daha yüksek getiri dönemlerinin telafi ettiği anlamına gelir. , örneğin birçok mevsimlik işletmede olduğu gibi.

kavramsal arka plan

Basit bir örnek düşünün: bir öğrenci sınıfı, bir konuda 100 maddelik doğru/yanlış testine giriyor. Tüm öğrencilerin tüm soruları rastgele seçtiğini varsayalım. Daha sonra, her öğrencinin puanı , beklenen ortalaması 50 olan bir dizi bağımsız ve aynı şekilde dağılmış rasgele değişkenlerden birinin gerçekleşmesi olacaktır . Doğal olarak, bazı öğrenciler şans eseri önemli ölçüde 50'nin üzerinde ve bazıları da önemli ölçüde 50'nin altında puan alacaktır. Öğrencilerin sadece en yüksek puanı alan %10'unu seçer ve onlara tüm maddelerde tekrar rastgele seçtikleri ikinci bir test verirse, ortalama puanın yine 50'ye yakın olması beklenir. Böylece bu öğrencilerin ortalaması "gerilemiş" olur. "Orijinal sınava giren tüm öğrencilerin ortalamasına kadar. Bir öğrencinin orijinal testte aldığı puan ne olursa olsun, ikinci testteki puanının en iyi tahmini 50'dir.

Test sorularına cevap seçmek rastgele değilse – örneğin, öğrenciler tarafından verilen cevaplarda şans (iyi veya kötü) veya rastgele tahminler söz konusu değilse – o zaman tüm öğrencilerin ikinci testte de aynı puanı almaları beklenirdi. orijinal testte puanlanır ve ortalamaya doğru bir gerileme olmaz.

Çoğu gerçekçi durum, bu iki uç nokta arasında yer alır: örneğin, sınav puanlarını beceri ve şansın bir bileşimi olarak düşünebiliriz . Bu durumda, ortalamanın üzerinde puan alan öğrencilerin alt kümesi, yetenekli ve özellikle şanssızlığı olmayanlar ile vasıfsız ancak son derece şanslı olanlardan oluşacaktır. Bu alt kümenin yeniden test edilmesinde, vasıfsızların şanslarını tekrarlamaları pek olası değilken, yetenekli olanlar şanssızlık için ikinci bir şansa sahip olacaklar. Bu nedenle, orijinali tekrarlanamasa bile, daha önce başarılı olanların ikinci testte de pek başarılı olmaları olası değildir.

Aşağıdaki, ortalamaya doğru bu ikinci tür regresyonun bir örneğidir. Bir öğrenci sınıfı, birbirini izleyen iki günde aynı testin iki sürümünü alır. İlk gün en kötü performans gösterenlerin ikinci gün puanlarını artırma eğiliminde oldukları ve ilk gündeki en iyi performans gösterenlerin ikinci gün daha kötü performans gösterme eğiliminde oldukları sıklıkla gözlemlenmiştir. Bu fenomen, öğrenci puanlarının kısmen altta yatan yetenek ve kısmen de şansa göre belirlenmesinden kaynaklanmaktadır. İlk test için, bazıları şanslı olacak ve yeteneklerinden daha fazla puan alacak, bazıları ise şanssız olacak ve yeteneklerinden daha az puan alacak. İlk testteki şanslı öğrencilerin bir kısmı ikinci testte yine şanslı olacak, ancak çoğu (onlar için) ortalama veya ortalamanın altında puanlara sahip olacak. Bu nedenle, şanslı olan ve ilk testte yeteneklerinin üzerinde performans gösteren bir öğrencinin, ikinci testte daha iyi bir puandan daha kötü bir puan alması daha olasıdır. Benzer şekilde, şanssız bir şekilde ilk testte yeteneklerinden daha az puan alan öğrenciler, ikinci testte puanlarının arttığını görme eğiliminde olacaktır. Bir ekstrem olayın meydana gelmesinde şansın etkisi ne kadar büyük olursa, şansın birden fazla olayda kendini tekrar etmesi o kadar az olasıdır.

Diğer örnekler

Favori spor takımınız geçen yıl şampiyonluğu kazandıysa, gelecek sezon kazanma şansları için bu ne anlama geliyor? Bu sonucun yetenekten kaynaklandığı ölçüde (takım iyi durumda, en iyi teknik direktörle vs.), galibiyetleri gelecek yıl tekrar kazanma ihtimalinin daha yüksek olduğunu gösteriyor. Ancak bu şanstan ne kadar büyük olursa (uyuşturucu skandalına karışan diğer takımlar, avantajlı beraberlik, seçimlerin verimli olduğu ortaya çıktı vb.), gelecek yıl tekrar kazanma olasılıkları o kadar az olur.

Bir tıbbi deneme, belirli bir ilacın veya tedavinin, bir durum için diğer tüm tedavilerden daha iyi performans gösterdiğini ileri sürerse, ikinci bir denemede, daha iyi performans gösteren ilacın veya tedavinin ortalamaya daha yakın performans göstermesi daha olasıdır.

Bir ticari kuruluş, performansının değişmemesinin altında yatan nedenlere rağmen, oldukça kârlı bir çeyreğe sahipse, bir sonraki çeyrekte daha az başarılı olması muhtemeldir.

Çaylak sezonlarında başarılı olan beyzbol oyuncularının ikinci sezonlarında daha kötü performans göstermeleri muhtemeldir; " İkinci sınıf çöküşü ". Benzer şekilde, ortalamaya doğru gerileme, Sports Illustrated kapak uğursuzluğu için bir açıklamadır - kapak özelliğiyle sonuçlanan istisnai performans dönemlerini, muhtemelen daha vasat performans dönemleri izleyecek ve kapakta görünmenin bir sporcunun düşüşüne neden olduğu izlenimini verecektir. .

Tarih

Regresyon kavramı genetikten gelir ve 19. yüzyılın sonlarında Sir Francis Galton tarafından kalıtsal boyutta vasatlığa doğru Regresyon'un yayınlanmasıyla popüler hale getirilmiştir . Galton, ebeveynlerdeki aşırı özelliklerin (örneğin boy) tamamen çocuklarına geçmediğini gözlemledi. Bunun yerine, yavrudaki özellikler vasat bir noktaya (o zamandan beri ortalama olarak tanımlanan bir noktaya) doğru geriler . Yüzlerce insanın boyunu ölçerek, ortalamaya gerilemeyi ölçebildi ve etkinin boyutunu tahmin edebildi. Galton, "yavruların ortalama gerilemesi, ilgili orta-ebeveyn sapmalarının sabit bir kısmıdır" diye yazdı . Bu, bir çocuk ve ebeveynleri arasındaki bazı özelliklerdeki farkın, ebeveynlerinin popülasyondaki tipik insanlardan sapması ile orantılı olduğu anlamına gelir. Ebeveynlerinin her biri, erkek ve kadınların ortalamalarından iki inç daha uzunsa, o zaman, yavru, ebeveynlerinden bir faktörle (bugün, bir eksi regresyon katsayısı diyeceğiz ) iki inç çarpı iki inçten daha kısa olacaktır. Boy için, Galton bu katsayının yaklaşık 2/3 olduğunu tahmin etti: Bir bireyin boyu, ebeveynlerin popülasyon ortalamasından sapmasının üçte ikisi olan bir orta nokta etrafında ölçülecektir.

Galton, "gerileme" terimini, çok faktörlü nicel genetik özelliklerin kalıtımında gözlemlenebilir bir gerçeği tanımlamak için icat etti : yani dağılımın sonunda bulunan ebeveynlerin yavruları, merkeze, ortalamaya daha yakın olma eğiliminde olacaklar. dağıtım. Bu eğilimi nicelleştirdi ve bunu yaparken doğrusal regresyon analizini icat etti , böylece modern istatistiksel modellemenin çoğunun temelini attı. O zamandan beri, "gerileme" terimi çeşitli anlamlar kazanmıştır ve modern istatistikçiler tarafından , Galton'un genetik alanındaki orijinal gözlemleriyle çok az ilgisi olan örnekleme yanlılığı fenomenini tanımlamak için kullanılabilir .

Matematiksel analizi doğru olmasına rağmen, Galton'un gözlemlediği regresyon fenomeni için biyolojik açıklamasının artık yanlış olduğu biliniyor. Dedi ki: "Bir çocuk kısmen ebeveynlerinden, kısmen atalarından miras alır. Genel olarak konuşursak, soyağacı ne kadar geriye giderse, ataları gelişigüzel alınan eşit sayıdaki herhangi bir örnekten farklı olmayı bırakana kadar, o kadar çok ve çeşitli olacaktır. genel olarak yarıştan." Bu yanlıştır, çünkü bir çocuk genetik yapısını sadece ebeveynlerinden alır. Genetik materyalde nesil atlaması yoktur: Daha önceki atalardan gelen herhangi bir genetik materyal, ebeveynlerden geçmiş olmalıdır ( onlarda ifade edilmemiş olabilir ). Kalıtsal özelliğin (örneğin boy) çok sayıda çekinik gen tarafından kontrol edildiğini varsayarsak, fenomen daha iyi anlaşılır . İstisnai olarak uzun boylu bireyler , bu lokusların büyük bir kısmında artan yükseklik mutasyonları için homozigot olmalıdır . Ancak bu mutasyonları taşıyan lokuslar, iki uzun birey arasında mutlaka paylaşılmaz ve bu bireyler çiftleşirse, yavruları, ebeveynlerinden daha az lokusta "uzun" mutasyonlar için ortalama olarak homozigot olacaktır. Ek olarak, boy tamamen genetik olarak belirlenmez, aynı zamanda gelişim sırasındaki çevresel etkilere de maruz kalır ve bu da istisnai ebeveynlerin yavrularının ebeveynlerinden daha ortalamaya daha yakın olmalarını sağlar.

Ortalamaya gerilemenin bu popülasyon genetik fenomeni, en iyi, iki terimli olarak dağıtılmış bir kalıtım sürecinin ve normal olarak dağıtılan çevresel etkilerin bir kombinasyonu olarak düşünülür. Buna karşılık, "ortalama gerileme" terimi, şimdi , yeni, tekrarlanan veya daha büyük numunelerin, gerçek temel popülasyon ortalamasına daha yakın olan numune araçlarını gösterdiği için bir ilk örnekleme yanlılığının ortadan kalkabileceği olgusunu tanımlamak için sıklıkla kullanılmaktadır .

Önem

Ortalamaya doğru regresyon , deneylerin tasarımında önemli bir husustur .

Kalp krizi geçirme riski açısından incelenen ve puanlanan, benzer yaştaki 1000 kişiden oluşan varsayımsal bir örnek alın. İstatistikler, en büyük risk altında derecelendirilen 50 kişiye yapılan bir müdahalenin başarısını ölçmek için kullanılabilir. Müdahale diyet, egzersiz veya ilaç tedavisinde bir değişiklik olabilir. Müdahaleler değersiz olsa bile, test grubunun ortalamaya doğru gerileme nedeniyle bir sonraki fizik muayenesinde bir gelişme göstermesi beklenir. Bu etkiyle mücadele etmenin en iyi yolu, grubu rastgele tedavi alan bir tedavi grubuna ve almayan bir kontrol grubuna bölmektir . Tedavi, ancak tedavi grubu kontrol grubundan daha fazla gelişirse etkili olarak değerlendirilecektir.

Alternatif olarak, bir grup dezavantajlı çocuk, üniversite potansiyeli en yüksek olanları belirlemek için test edilebilir. En üstteki %1'lik kısım belirlenebilir ve özel zenginleştirme kursları, özel ders, danışmanlık ve bilgisayarlarla sağlanabilir. Program etkili olsa bile, test bir yıl sonra tekrarlandığında ortalama puanları daha düşük olabilir. Ancak bu koşullarda, özel ihtiyaçları göz ardı edilen dezavantajlı çocuklardan oluşan bir kontrol grubuna sahip olmak etik dışı kabul edilebilir. Kontrol grubu yöntemi kadar güvenilir olmasa da, büzülme için matematiksel bir hesaplama bu etkiyi ayarlayabilir (ayrıca Stein'in örneğine bakınız ).

Etki, genel çıkarım ve tahmin için de kullanılabilir. Bugün ülkedeki en sıcak yerin, bugün ile karşılaştırıldığında, yarın sıcaktan çok daha soğuk olması muhtemeldir. Son üç yıldaki en iyi performans gösteren yatırım fonunun, önümüzdeki üç yıl içinde iyileşmekten ziyade göreceli performans düşüşü görmesi daha olasıdır. Bu yılın en başarılı Hollywood aktörü, bir sonraki filmi için büyük olasılıkla daha az brüt elde edecek. All-Star arasında en yüksek vuruş ortalamasına sahip beyzbol oyuncusu, sezonun ikinci yarısında daha yüksek bir ortalamadan daha düşük bir ortalamaya sahip olacak.

yanlış anlamalar

Ortalamaya doğru gerileme kavramı çok kolaylıkla kötüye kullanılabilir.

Yukarıdaki öğrenci testi örneğinde, dolaylı olarak ölçülenin iki ölçüm arasında değişmediği varsayılmıştır. Ancak, dersin geçti/kaldı olduğunu ve öğrencilerin geçmek için her iki testte de 70'in üzerinde puan almaları gerektiğini varsayalım. O zaman, ilk seferde 70'in altında puan alan öğrenciler, başarılı olmak için hiçbir teşvike sahip olmayacak ve ikinci kez ortalama olarak daha kötü puan alabileceklerdir. Öte yandan, 70 yaşın üzerindeki öğrenciler, sınava girerken ders çalışmak ve konsantre olmak için güçlü bir teşvike sahip olacaklardır. Bu durumda 70'ten uzaklaşma , altındaki puanların düştüğü ve üstündeki puanların yükseldiği görülebilir. Ölçüm süreleri arasındaki değişikliklerin, ortalamaya doğru gerileme istatistiksel eğilimini artırması, dengelemesi veya tersine çevirmesi mümkündür.

Ortalamaya doğru istatistiksel regresyon nedensel bir fenomen değildir . İlk gün testte en kötü puanı alan bir öğrenci, etki nedeniyle ikinci gün puanını önemli ölçüde artırmaz. Ortalama olarak, en kötü golcüler gelişir, ancak bu sadece doğrudur, çünkü en kötü golcülerin şanstan çok şanssız olmaları daha olasıdır. Bir puanın rastgele belirlendiği ölçüde veya bir puanın, öğrencinin akademik yeteneği veya "gerçek bir değer" olması ile belirlenmediğinin aksine, rastgele değişkenliği veya hatası olduğu ölçüde, fenomenin bir etkisi olacaktır. Bu konuda klasik bir hata eğitimdeydi. İyi çalışması için övgü alan öğrencilerin bir sonraki ölçekte daha kötü yaptıkları ve kötü çalışması nedeniyle cezalandırılan öğrencilerin bir sonraki ölçekte daha iyi yaptıkları fark edildi. Eğitimciler bu temelde övmeyi bırakıp cezalandırmaya devam etmeye karar verdiler. Böyle bir karar bir hataydı, çünkü ortalamaya doğru gerileme neden ve sonuca değil, bir ortalama etrafındaki doğal dağılımdaki rastgele hataya dayalıdır.

Aşırı bireysel ölçümler ortalamaya doğru gerilese de, ikinci ölçüm örneği ortalamaya birinciden daha yakın olmayacaktır. Öğrencileri tekrar düşünün. Aşırı bireylerin eğiliminin, ortalama 80'e doğru yolun %10'unda gerilemek olduğunu varsayalım , bu nedenle, ilk gün 100 puan alan bir öğrencinin ikinci gün 98 puan alması beklenir ve ilk gün 70 puan alan bir öğrencinin puan alması beklenir. ikinci gün 71 puan. Bu beklentiler ortalamaya ilk gün puanlarından daha yakındır. Ancak ikinci gün puanları beklentilerine göre değişecektir; bazıları daha yüksek, bazıları daha düşük olacak. Ayrıca ortalamaya çok yakın ölçüm yapan bireylerin ortalamadan uzaklaşmayı beklemeleri gerekir. Etki, ortalamaya doğru gerilemenin tam tersidir ve onu tam olarak dengeler. Dolayısıyla uç bireyler için ikinci puanın ortalamaya ilk puandan daha yakın olmasını bekleriz, ancak tüm bireyler için ortalamadan uzaklıkların dağılımının her iki ölçüm grubunda da aynı olmasını bekleriz.

Yukarıdaki noktayla ilgili olarak, ortalamaya doğru gerileme her iki yönde de eşit derecede iyi çalışır. İkinci gün test puanı en yüksek olan öğrencinin ilk gün daha kötü sonuç almasını bekliyoruz. Ve ilk günkü en iyi öğrenciyi ikinci gündeki en iyi öğrenciyle karşılaştırırsak, aynı birey olup olmadığına bakılmaksızın, her iki yönde de ortalamaya doğru bir gerileme eğilimi vardır. Her iki günde de en iyi skorların ortalamadan eşit derecede uzak olmasını bekliyoruz.

Regresyon yanılgıları

Çoğu fenomen, ortalamaya gerileme hesaba katılmadığında yanlış nedenlere atfedilme eğilimindedir.

Bunun uç bir örneği, Horace Secrist'in 1933 tarihli The Triumph of Mediocrity in Business adlı kitabıdır . Aslında böyle bir etkisi yoktur; kar oranlarının değişkenliği zaman içinde neredeyse sabittir. Secrist, yalnızca ortalamaya doğru ortak gerilemeyi tanımlamıştı. Bıkkın bir eleştirmen olan Harold Hotelling , kitabı "filleri satırlar ve sütunlar halinde düzenleyerek çarpım tablosunu kanıtlamaya ve daha sonra aynı şeyi çok sayıda başka hayvan türü için yapmaya" benzetmiştir.

Massachusetts'teki standartlaştırılmış eğitim testlerinde "iyileştirme puanlarının" hesaplanması ve yorumlanması, muhtemelen regresyon yanılgısının başka bir örneğini sağlar. 1999'da okullara iyileştirme hedefleri verildi. Her okul için, Eğitim Bakanlığı 1999 ve 2000 yıllarında öğrencilerin elde ettiği ortalama puandaki farkı tablolaştırdı. En kötü performans gösteren okulların çoğunun hedeflerine ulaştığı hemen fark edildi ve Eğitim Bakanlığı bunu teyit olarak kabul etti. politikalarının sağlamlığı. Bununla birlikte, Brookline Lisesi (18 Ulusal Başarı Bursu finalisti ile) gibi Commonwealth'deki sözde en iyi okulların çoğunun başarısız olduğu ilan edildi. İstatistik ve kamu politikasını içeren birçok durumda olduğu gibi, konu tartışılmaktadır, ancak sonraki yıllarda "iyileştirme puanları" açıklanmamıştır ve bulgular ortalamaya gerileme vakası gibi görünmektedir.

2002 Nobel İktisadi Bilimler Anma Ödülü sahibi psikolog Daniel Kahneman , ortalamaya gerilemenin, azarlamaların neden performansı iyileştirdiğini açıklayabileceğine işaret ederken, övgü geri tepiyor gibi görünüyor.

Beceri öğrenmeyi teşvik etmek için övgünün cezadan daha etkili olduğunu uçuş eğitmenlerine öğretmeye çalışırken kariyerimin en tatmin edici Eureka deneyimini yaşadım. Coşkulu konuşmamı bitirdiğimde, dinleyiciler arasındaki en deneyimli eğitmenlerden biri elini kaldırdı ve olumlu pekiştirmenin kuşlar için iyi olabileceğini kabul ederek başlayan, ancak bunun optimal olduğunu inkar eden kendi kısa konuşmasını yaptı. uçuş öğrencileri için. "Birçok kez uçuş öğrencilerini bazı akrobasi manevralarını temiz bir şekilde yerine getirdikleri için övdüm ve genel olarak tekrar denediklerinde daha da kötüleşiyorlar. Öte yandan, öğrencilere kötü infaz için sık sık çığlık attım ve genel olarak bir dahaki sefere daha iyi yapıyorlar. O yüzden lütfen bize pekiştirmenin işe yarayıp cezanın işe yaramadığını söyleme çünkü durum tam tersi." Bu, dünyayla ilgili önemli bir gerçeği anladığım neşeli bir andı: çünkü başkalarını iyi yaptıklarında ödüllendirmeye ve kötü yaptıklarında cezalandırmaya meyilliyiz ve ortalamaya gerileme olduğu için bu, insanın bir parçasıdır. başkalarını ödüllendirdiğimiz için istatistiksel olarak cezalandırılmamız ve onları cezalandırdığımız için ödüllendirilmemiz koşulu. Hemen, her katılımcının herhangi bir geri bildirim olmaksızın bir hedefe iki madeni para attığı bir gösteri düzenledim. Hedefe olan mesafeleri ölçtük ve ilk seferde en iyisini yapanların ikinci denemelerinde çoğunlukla kötüleştiğini ve tam tersini gördük. Ama bu gösterinin ömür boyu ters bir ihtimale maruz kalmanın etkilerini geri alamayacağını biliyordum.

Kahneman'ın hikayesini basit terimlerle ifade etmek gerekirse, biri ciddi bir hata yaptığında, performansları daha sonra genellikle ortalama seviyelerine geri dönecektir. Bu, bir gelişme ve eleştirmenin övmekten daha iyi olduğuna dair bir inancın "kanıtı" olarak görünecektir (özellikle o "düşük" anda eleştirmeye istekli olan herkes tarafından kabul edilir). Tam tersi durumda, ortalamanın üzerinde bir performans sergilendiğinde, performansları da daha sonra ortalama seviyelerine geri dönme eğiliminde olacaktır; değişiklik, bir bozulma olarak algılanacak ve ilk performansın ardından herhangi bir ilk övgü, bu bozulmanın bir nedeni olarak algılanacaktır. Sırf eleştirme ya da övme, ortalamaya doğru gerilemeden önce geldiği için, eleştirme ya da övme eylemine yanlış bir nedensellik atfedilir. Regresyon yanılgı da açıklanmıştır Rolf Dobelli 's Açıkçası Düşünme Sanatı .

Birleşik Krallık yasa uygulama politikaları , kazaların olduğu kara noktalarda statik veya mobil hız kameralarının görünür şekilde yerleştirilmesini teşvik etmiştir . Bu politika, bir kamera kurulduktan sonra ciddi trafik kazalarında buna karşılık gelen bir azalma olduğu algısıyla doğrulandı . Bununla birlikte, istatistikçiler, kurtarılan hayatlarda net bir fayda olmasına rağmen, ortalamaya gerilemenin etkilerinin dikkate alınmamasının, faydalı etkilerin abartılmasına yol açtığına işaret etmişlerdir.

İstatistiksel analistler, sporda ortalamaya gerilemenin etkisini uzun zamandır fark ettiler; Hatta buna özel bir adları bile var: " ikinci sınıf çöküşü ". Örneğin, Carmelo Anthony ve NBA 'in Denver Nuggets 2005 yılında Anthony numaraları çaylak sezonu düşmüştü: Onun bunu tekrarlamak beklenemez diye olağanüstü 2004 yılında olağanüstü bir çaylak sezonu geçirdi. "İkinci sınıf çöküşü"nün nedenleri çoktur, çünkü spor uyum ve karşı ayarlamaya dayanır, ancak bir çaylak olarak şansa dayalı mükemmellik, herkes kadar iyi bir nedendir. Spor performansında ortalamaya gerileme, görünen " Sports Illustrated kapak uğursuzluğu " nu ve " Madden Laneti " ni de açıklayabilir . John Hollinger , ortalamaya gerileme fenomeni için alternatif bir isme sahiptir: "fluke kuralı", Bill James ise buna "Plexiglas Prensibi" adını verir .

Popüler bilgi, sporcuların bir sezondan diğerine düşen performansının bir açıklaması olarak ortalamaya doğru gerilemeye odaklandığından, genellikle bu tür bir gerilemenin performansın artmasını da hesaba katabileceği gerçeğini gözden kaçırmıştır. Örneğin, bir sezondaki Beyzbol Ligi oyuncularının vuruş ortalamasına bakıldığında , vuruş ortalaması lig ortalamasının üzerinde olanlar, bir sonraki yıl ortalamaya doğru aşağı doğru gerileme eğilimi gösterirken, vuruş ortalaması ortalamanın altında olanlar, ortalamanın altında kalma eğilimindedir. ertesi yıl ortalamaya doğru yukarı doğru ilerler.

Diğer istatistiksel olaylar

Ortalamaya doğru regresyon basitçe, aşırı rastgele bir olayı takiben, bir sonraki rastgele olayın muhtemelen daha az aşırı olacağını söyler. Gelecekteki olay hiçbir şekilde önceki olayı "telafi etmez" veya "eşitlemez", ancak bunun kumarbazın yanılgısında (ve değişken ortalamalar yasasında ) varsayılır . Benzer şekilde, büyük sayılar yasası , uzun vadede ortalamanın beklenen değere yöneleceğini belirtir, ancak bireysel denemeler hakkında hiçbir açıklama yapmaz. Örneğin, adil bir yazı turasında 10 turalık bir turdan sonra (nadir, aşırı bir olay), ortalamaya gerileme, bir sonraki tura sayısının muhtemelen 10'dan az olacağını belirtirken, büyük sayılar yasası şunu belirtir: uzun vadede, bu olayın ortalaması büyük olasılıkla olacak ve turaların ortalama oranı 1/2 eğiliminde olacaktır. Buna karşılık, kumarbazın yanılgısı, madalyonun artık bir kuyruk dizisinin dengelenmesi için "vadesi geldiğini" yanlış bir şekilde varsayar.

Ters etki, sonsuza doğru kaybolmayan olasılık yoğunluğuna sahip bir dağılımdan kaynaklanan kuyruğa gerilemedir.

Veri noktalarının basit doğrusal regresyonu için tanım

Bu, Sir Francis Galton'un orijinal kullanımını yakından takip eden, ortalamaya doğru gerilemenin tanımıdır .

Diyelim ki n tane veri noktası var { y _ben , x _ben }, burada i  = 1, 2, ..., n . Regresyon çizgisinin denklemini , yani düz çizgiyi bulmak istiyoruz.

${\displaystyle y=\alpha +\beta x,\,}$

hangi veri noktaları için "en iyi" bir uyum sağlayacaktır. (Verilen veri noktaları için düz bir çizginin uygun regresyon eğrisi olmayabileceğini unutmayın.) Burada "en iyi", en küçük kareler yaklaşımında olduğu gibi anlaşılacaktır : lineer regresyonun kare artıklarının toplamını en aza indiren böyle bir çizgi modeli. Başka bir deyişle, α ve β sayıları aşağıdaki minimizasyon problemini çözer:

Bul , nerede${\displaystyle \min _{\alpha ,\,\beta }Q(\alpha ,\beta )}$${\displaystyle Q(\alpha ,\beta )=\sum _{i=1}^{n}{\hat {\varepsilon }}_{i}^{\,2}=\sum _{i=1 }^{n}(y_{i}-\alpha -\beta x_{i})^{2}\ }$

Kullanma taşı bu gösterilebilir ki değerleri α ve β bu amaç fonksiyonu minimize S olan

${\displaystyle {\begin{hizalı}&{\hat {\beta }}={\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})( y_{i}-{\bar {y}})}{\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}={\ frac {{\overline {xy}}-{\bar {x}}{\bar {y}}}{{\overline {x^{2}}}-{\bar {x}}^{2}} }={\frac {\operatöradı {Cov} [x,y]}{\operatöradı {Var} [x]}}=r_{xy}{\frac {s_{y}}{s_{x}}}, \\&{\hat {\alpha }}={\bar {y}}-{\hat {\beta }}\,{\bar {x}},\end{hizalı}}}$

burada r, _xy olan numune korelasyon katsayıları arasındaki x ve y , s _x olan standart sapması ve x ve s _y uygun standart sapmasıdır y . Bir değişken üzerindeki yatay çubuk, o değişkenin örnek ortalaması anlamına gelir. Örneğin:${\displaystyle {\overline {xy}}={\tfrac {1}{n}}\textstyle \sum _{i=1}^{n}x_{i}y_{i}\ .}$

Yukarıdaki ifadeleri yerine ve içine yerleştirmek, uygun değerleri verir ${\ Displaystyle {\ şapka {\ alfa }}}$${\displaystyle {\hat {\beta }}}$${\displaystyle y=\alpha +\beta x,\,}$

${\displaystyle {\hat {y}}={\hat {\alpha }}+{\hat {\beta }}x,\,}$

hangi verim

${\displaystyle {\frac {{\hat {y}}-{\bar {y}}}{s_{y}}}=r_{xy}{\frac {x-{\bar {x}}}{\displaystyle {\frac {{\hat {y}}} s_{x}}}}$

Bu, standartlaştırılmış veri noktalarının regresyon çizgisinde r _xy'nin oynadığı rolü gösterir .

-1 <  r _xy  < 1 ise, veri noktalarının ortalamaya doğru gerileme gösterdiğini söyleriz. Başka bir deyişle, örnek korelasyon katsayısı mükemmel olmayan bir dizi veri noktası için doğrusal regresyon uygun model ise, ortalamaya doğru bir regresyon vardır. Tahmin edilen (veya uydurulan) standartlaştırılmış y değeri , ortalamasına, x'in standartlaştırılmış değerinin ortalamasına olduğundan daha yakındır .

Aynı marjinal dağılımlara sahip iki değişkenli dağıtım tanımları

kısıtlayıcı tanım

Let X ₁ , X ₂ be rastgele değişkenler , ortalama özdeş marjinal dağılımına sahip ^ ı . Bu kayıt altına alınmasında, ikili dağılım içinde X ₁ ve X ₂ sergi söylenen ortalama doğru gerileme her sayı için, eğer c  >  u , elimizdeki

μ  ≤ E[ X ₂  | X ₁  =  c ] <  c ,

c  <  μ için tutan ters eşitsizliklerle .

Aşağıdaki, yukarıdaki tanımın resmi olmayan bir açıklamasıdır. Bir widget popülasyonu düşünün . Her parçacığın iki sayısı vardır, X ₁ ve X ₂ (örneğin, sol yayılma alanı ( X ₁ ) ve sağ yayılma alanı ( X ₂ )). Popülasyondaki X ₁ ve X ₂ olasılık dağılımlarının aynı olduğunu ve X ₁ ve X ₂ ortalamalarının her ikisinin de μ olduğunu varsayalım . Şimdi popülasyondan rastgele bir parçacık alıyoruz ve X ₁ değerini c ile gösteriyoruz . (Not bu C 'ye eşit veya daha küçük, daha büyük olabilir u .) Bu eklendi en değerine erişemezler x ₂ yapılmamış. Let d göstermektedirler beklenen değerini X ₂ , bu, belirli bir alette arasında. ( Yani Let d ortalama değerini belirtmektedir X ₂ ile popülasyondaki tüm aletler arasında X ₁ = c .) Aşağıdaki koşul doğru ise:

Değeri ne olursa olsun C olan, d arasında durmaktadır ^ ı ve c ( yani d daha yakın olan u daha C olan),

o zaman X ₁ ve X _2'nin ortalamaya doğru gerileme gösterdiğini söyleriz .

Bu tanım, "ortalamaya doğru gerileme" teriminin Galton'un orijinal kullanımından evrimleşmiş mevcut yaygın kullanımıyla yakından uyumludur. Aynı marjinal dağılımlara sahip her iki değişkenli dağılımın (bu tanım altında) ortalamaya doğru gerileme göstermemesi anlamında "kısıtlayıcıdır".

teorem

Bir çift (durumunda X ,  Y, rastgele değişkenin) aşağıda belirtildiği gibi iki değişkenli normal dağılım , daha sonra koşullu ortalama D ( Y | X ) 'in bir doğrusal fonksiyonudur X . Korelasyon katsayısı r arasında X ve Y marjinal araçlar ile birlikte, ve sapmalar X ve Y , bu doğrusal ilişkiyi belirler:

${\displaystyle {\frac {E(Y\mid X)-E[Y]}{\sigma _{y}}}=r{\frac {XE[X]}{\sigma _{x}}}, }$

burada E[X] ve E[Y] , sırasıyla X ve Y'nin beklenen değerleridir ve σ _x ve σ _y , sırasıyla X ve Y'nin standart sapmalarıdır .

Bu nedenle koşullu beklenen değer Y göz önüne alındığında, X, bir T standart sapma olarak ortalama yukarıda (ve ne zaman, onun ortalaması aşağıdaki nerede olduğu durumu da içerir t  <0), bir oda sıcaklığı ortalama üzerinde standart sapmalar Y . beri | r | ≤ 1, Y , standart sapma sayısıyla ölçüldüğü gibi , ortalamadan X'ten daha uzak değildir .

Dolayısıyla, eğer 0 ≤  r  < 1 ise, ( X ,  Y ) ortalamaya doğru (bu tanımla) regresyon gösterir.

Genel tanım

Aşağıdaki ortalamaya geri dönüş tanımı, Samuels tarafından , yukarıdaki ortalamaya doğru gerilemenin daha kısıtlayıcı tanımına bir alternatif olarak önerilmiştir .

Let X ₁ , X ₂ be rastgele değişkenler , ortalama özdeş marjinal dağılımına sahip ^ ı . Bu kayıt altına alınmasında, ikili dağılım içinde X ₁ ve X ₂ sergi söylenir ortalama doğru reversion her sayı için, eğer c , elimizdeki

μ  ≤ E[ X ₂  | X ₁  >  c ] < E[ X ₁  | X ₁  >  c ] ve

μ  ≥ E[ X ₂  | X ₁  <  c ] > E[ X ₁  | X ₁  <  c ]

Bu tanım, aynı marjinal dağılımlara sahip her iki değişkenli dağılımın ortalamaya doğru geri dönüş sergilemesi anlamında "genel"dir .

Ayrıca bakınız

• Hardy-Weinberg ilkesi
• İçsel geçerlilik
• büyük sayılar yasası
• Martingal
• regresyon seyreltme
• seçim yanlılığı

Referanslar

daha fazla okuma

• JM Bland ve DG Altman (Haziran 1994). "İstatistik Notları: Ortalamaya doğru gerileme" . İngiliz Tıp Dergisi . 308 (6942): 1499. doi : 10.1136/bmj.308.6942.1499 . PMC  2540330 . PMID  8019287 . Galton'un orijinal verilerinin bir diyagramını içeren makale.

• Michael R. Chernick ve Robert H. Friis (2003). Sağlık Bilimlerine Giriş Biyoistatistiği . Wiley-Interscience . P. 272. ISBN 978-0-471-41137-6.

• Edward J. Dudewicz ve Satya N. Mishra (1988). "Bölüm 14.1: Regresyon parametrelerinin tahmini; Doğrusal modeller". Modern Matematiksel İstatistik . John Wiley ve Oğulları . ISBN'si 978-0-471-81472-6.

• Francis Galton (1886). "Kalıtsal boyda sıradanlığa doğru gerileme" (PDF) . Büyük Britanya ve İrlanda Antropoloji Enstitüsü Dergisi . 15 : 246-263. doi : 10.2307/2841583 . JSTOR  2841583 .

• Donald F. Morrison (1967). "Bölüm 3: Çok Değişkenli Normal Popülasyondan Örnekler". Çok Değişkenli İstatistiksel Yöntemler . McGraw-Hill . ISBN'si 978-0-534-38778-5.

• Stephen M. Stigler (1999). "Bölüm 9". Tablodaki İstatistikler . Harvard Üniversitesi Yayınları .

• Myra L. Samuels (Kasım 1991). "Ortalamaya Doğru İstatistiksel Geri Dönüş: Ortalamaya Doğru Gerilemeden Daha Evrensel". Amerikan İstatistikçisi . 45 (4): 344-346. doi : 10.2307/2684474 . JSTOR  2684474 .
• Stephen Senn. Regresyon: Eski Bir Anlam için Yeni Bir Mod , The American Statistician , Cilt 44, Sayı 2 (Mayıs 1990), s. 181-183.
• David C. Schmittlein. Şaşırtıcı olmayan Gözlemlerden Şaşırtıcı Çıkarımlar: Koşullu Beklentiler gerçekten Ortalamaya geriliyor mu? Amerikan İstatistikçisi , Cilt 43, Sayı 3 (Ağustos 1989), s. 176-183.
• Ortalamaya Doğru Regresyon ve Değişim Çalışması , Psikolojik Bülten
• Ortalamaya doğru gerilemenin matematiksel olmayan bir açıklaması.
• Ortalamaya doğru bir gerileme simülasyonu.
• Amanda Wachsmuth, Leland Wilkinson, Gerard E. Dallal. Galton's Bend: Galton'un Aile Boyu Regresyon Verilerinde Keşfedilmemiş Doğrusal Olmayan Bir Şey ve Pearson ve Lee'nin Boy Verilerine Dayalı Muhtemel Bir Açıklama (Galton'un analizine modern bir bakış.)
• Bir istatistikçi tarafından bir regresyon örneği olarak yorumlanan Massachusetts standartlaştırılmış test puanları: bkz . sci.stat.edu ve devamındaki tartışma .
• Gary Smith , What the Luck: The Surprising Role in Our Everyday Lives, New York: Overlook, Londra: Duckworth. ISBN  978-1-4683-1375-8 .

Dış bağlantılar

• Wikimedia Commons'ta Ortalamaya Doğru Gerileme ile ilgili medya