Ayrık küme veri yapısı - Disjoint-set data structure

Ayrık küme/Birlik bulma Ormanı
Tip	çok yollu ağaç
İcat edilmiş	1964
Tarafından icat edildi	Bernard A. Galler ve Michael J. Fischer
Zaman karmaşıklığı içinde büyük Ç gösterimde
algoritma Ortalama En kötü durumda Uzay O( n ) O( n ) Arama O( α ( n )) O( α ( n )) Birleştirmek O( α ( n )) O( α ( n ))

Gelen bilgisayar bilimleri , bir ayrık kümesi veri yapısı , aynı zamanda bir denilen birlik-Bul veri yapısı veya birleştirme-bulmak seti , mağazalar koleksiyonu olduğu bir veri yapısıdır ayrık setleri (örtüşmeyen). Eşdeğer olarak, bir kümenin bir bölümünü ayrık alt kümeler halinde saklar . Yeni kümeler ekleme, kümeleri birleştirme ( birlikleriyle değiştirme ) ve bir kümenin temsili bir üyesini bulma işlemlerini sağlar. Son işlem, herhangi iki elemanın aynı veya farklı kümelerde olup olmadığını verimli bir şekilde bulmayı sağlar.

Ayrık kümeli veri yapılarını uygulamanın birkaç yolu olsa da, uygulamada bunlar genellikle ayrık küme ormanı adı verilen belirli bir uygulamayla tanımlanır . Bu, sendikaları gerçekleştiren ve neredeyse sabit amortisman süresi içinde bulan özel bir orman türüdür. n düğümlü ayrık kümeli bir ormanda m toplama, birleştirme veya bulma işlemleri dizisi gerçekleştirmek için toplam O ( m α( n )) süresi gerekir ; burada α( n ) son derece yavaş büyüyen ters Ackermann işlevidir . Ayrık kümeli ormanlar, bu performansı işlem bazında garanti etmez. Bireysel birleştirme ve bulma işlemleri, sabit çarpı α( n ) zamanından daha uzun sürebilir , ancak her işlem, ardışık işlemlerin daha hızlı olması için ayrık küme ormanın kendisini ayarlamasına neden olur. Ayrık kümeli ormanlar hem asimptotik olarak optimaldir hem de pratik olarak verimlidir.

Ayrık kümeli veri yapıları , bir grafiğin minimum yayılan ağacını bulmak için Kruskal'ın algoritmasında önemli bir rol oynar . Minimum yayılan ağaçların önemi, ayrık kümeli veri yapılarının çok çeşitli algoritmaların altında yattığı anlamına gelir. Ek olarak, ayrık kümeli veri yapılarının, özellikle kayıt tahsis sorunları için derleyicilerde olduğu gibi sembolik hesaplama uygulamalarına da sahiptir .

Tarih

Ayrık-grubu ormanlar, ilk olarak tarif edilmiştir Bernard A. Galler ve Michael J. Fischer 1973 1964'te, kendi zaman karmaşıklığı ile sınırlandırılmıştır , tekrarlanan logaritma arasında göre, Hopcroft ve Ullman . 1975'te Robert Tarjan , algoritmanın zaman karmaşıklığı üzerindeki ( ters Ackermann fonksiyonu ) üst sınırını kanıtlayan ilk kişiydi ve 1979'da bunun sınırlı bir durum için alt sınır olduğunu gösterdi. 1989'da Fredman ve Saks , (amorti edilmiş) kelimelere işlem başına herhangi bir ayrık küme veri yapısı tarafından erişilmesi gerektiğini gösterdiler , böylece veri yapısının optimalliğini kanıtladılar. ${\ Displaystyle O(\log ^{*}(n))}$${\görüntüleme stili n}$${\görüntüleme stili O(m\alfa (n))}$${\görüntüleme stili \Omega (\alfa (n))}$

1991'de Galil ve Italiano, ayrık kümeler için veri yapılarının bir araştırmasını yayınladı.

1994'te Richard J. Anderson ve Heather Woll, Union–Find'ın hiçbir zaman engellemesi gerekmeyen paralelleştirilmiş bir versiyonunu tanımladılar.

2007 yılında, Sylvain Conchon ve Jean-Christophe Filliâtre , ayrık kümeli orman veri yapısının kalıcı bir versiyonunu geliştirerek yapının önceki sürümlerinin verimli bir şekilde korunmasına izin verdi ve ispat asistanı Coq'u kullanarak doğruluğunu resmileştirdi . Bununla birlikte, uygulama yalnızca geçici olarak kullanılırsa veya yapının aynı sürümü sınırlı geri izleme ile tekrar tekrar kullanılırsa asimptotiktir.

temsil

Ayrık kümeli bir ormandaki her düğüm, bir işaretçi ve bir boyut veya bir sıra (ancak her ikisi birden değil) gibi bazı yardımcı bilgilerden oluşur. İşaretçiler , bir ağacın kökü olmayan her düğümün üst öğeye işaret ettiği, üst işaretçi ağaçları yapmak için kullanılır . Kök düğümleri diğerlerinden ayırt etmek için, onların üst işaretçileri, düğüme dairesel bir başvuru veya bir sentinel değeri gibi geçersiz değerlere sahiptir. Her ağaç, kümenin üyeleri ağaçtaki düğümler olmak üzere ormanda depolanan bir kümeyi temsil eder. Kök düğümler küme temsilcileri sağlar: İki düğüm, ancak ve ancak düğümleri içeren ağaçların kökleri eşitse aynı kümededir.

Ormandaki düğümler, uygulamaya uygun herhangi bir şekilde depolanabilir, ancak yaygın bir teknik, onları bir dizide saklamaktır. Bu durumda, ebeveynler dizi indeksleri ile gösterilebilir. Her dizi girişi , ana işaretçi için Θ(lg n ) bit depolama gerektirir . Girişin geri kalanı için karşılaştırılabilir veya daha az miktarda depolama gerekir, bu nedenle ormanı depolamak için gereken bit sayısı Θ( n lg n ) olur . Bir uygulama sabit boyutlu düğümler kullanıyorsa (böylece depolanabilecek ormanın maksimum boyutunu sınırlar), bu durumda gerekli depolama n içinde doğrusaldır .

Operasyonlar

Ayrık küme veri yapıları üç işlemi destekler: Yeni bir öğe içeren yeni bir küme oluşturma; Belirli bir elemanı içeren kümenin temsilcisini bulma; ve İki kümeyi birleştirme.

Yeni setler yapmak

İşlem MakeSetyeni bir öğe ekler. Bu öğe, yalnızca yeni öğeyi içeren yeni bir kümeye yerleştirilir ve yeni küme, veri yapısına eklenir. Bunun yerine veri yapısı bir kümenin bölümü olarak görülüyorsa, MakeSetişlem yeni öğeyi ekleyerek kümeyi büyütür ve yeni öğeyi yalnızca yeni öğeyi içeren yeni bir alt kümeye koyarak mevcut bölümü genişletir.

Ayrık kümeli bir ormanda, MakeSetdüğümün üst işaretçisini ve düğümün boyutunu veya derecesini başlatır. Bir kök, kendisine işaret eden bir düğümle temsil ediliyorsa, bir öğenin eklenmesi aşağıdaki sözde kod kullanılarak açıklanabilir:

function MakeSet(x) is
    if x is not already in the forest then
        x.parent := x
        x.size := 1     // if nodes store size
        x.rank := 0     // if nodes store rank
    end if
end function

Bu işlem sabit zaman karmaşıklığına sahiptir. Özellikle, ayrık kümeli bir ormanı n düğümlü başlatmak için O ( n ) zaman gerekir.

Pratikte, x 'MakeSet i tutmak için bellek tahsis eden bir işlemden önce gelmelidir . İyi bir dinamik dizi uygulaması için olduğu gibi, bellek ayırma, amortize edilmiş bir sabit zamanlı işlem olduğu sürece, rastgele ayarlanmış ormanın asimptotik performansını değiştirmez.

Set temsilcilerini bulma

İşlem , bir kök öğeye ulaşana kadar Findbelirtilen bir sorgu düğümünden x üst işaretçileri zincirini takip eder . Bu kök eleman, x'in ait olduğu kümeyi temsil eder ve x'in kendisi olabilir . Findulaştığı kök öğeyi döndürür.

Bir Findoperasyonun yapılması ormanın iyileştirilmesi için önemli bir fırsat sunuyor. FindBir işlemdeki zaman, ana işaretçileri kovalamak için harcanır, bu nedenle daha düz bir ağaç daha hızlı Findişlemlere yol açar . a Findyürütüldüğünde, köke ulaşmanın her ana işaretçiyi art arda takip etmekten daha hızlı bir yolu yoktur. Ancak, bu arama sırasında ziyaret edilen ana işaretçiler, köke daha yakın işaret edecek şekilde güncellenebilir. Kök yolunda ziyaret edilen her öğe aynı kümenin parçası olduğundan, bu, ormanda depolanan kümeleri değiştirmez. Ancak Find, yalnızca sorgu düğümü ile kök arasındaki düğümler için değil, aynı zamanda onların soyundan gelenler için de gelecekteki işlemleri daha hızlı hale getirir . Bu güncelleme, ayrık küme ormanın itfa edilmiş performans garantisinin önemli bir parçasıdır.

FindAsimptotik olarak optimal zaman karmaşıklığını elde etmek için birkaç algoritma vardır . Yol sıkıştırma olarak bilinen bir algoritma ailesi , sorgu düğümü ile kök nokta arasındaki her düğümü köke yapar. Yol sıkıştırma, aşağıdaki gibi basit bir özyineleme kullanılarak uygulanabilir:

function Find(x) is
    if x.parent ≠ x then
        x.parent := Find(x.parent)
        return x.parent
    else
        return x
    end if
end function

Bu uygulama, biri ağaçtan yukarı, diğeri aşağı doğru olmak üzere iki geçiş yapar. Sorgu düğümünden köke giden yolu depolamak için yeterli kazı belleği gerektirir (yukarıdaki sözde kodda yol, çağrı yığını kullanılarak dolaylı olarak temsil edilir). Bu, her iki geçişi de aynı yönde gerçekleştirerek sabit miktarda belleğe düşürülebilir. Sabit bellek uygulaması, bir kez kökü bulmak için ve bir kez de işaretçileri güncellemek için sorgu düğümünden köke iki kez yürür:

function Find(x) is
    root := x
    while root.parent ≠ root do
        root := root.parent
    end while

    while x.parent ≠ root do
        parent := x.parent
        x.parent := root
        x := parent
    end while

    return root
end function

Tarjan ve Van LeeuwenFind , aynı en kötü durum karmaşıklığını koruyan ancak pratikte daha verimli olan tek geçişli algoritmalar da geliştirdiler . Bunlara yol bölme ve yol yarıya ayırma denir. Bunların her ikisi de sorgu düğümü ile kök arasındaki yoldaki düğümlerin üst işaretçilerini günceller. Yol bölme , o yoldaki her üst işaretçiyi düğümün büyük ebeveynine bir işaretçiyle değiştirir:

function Find(x) is
    while x.parent ≠ x do
        (x, x.parent) := (x.parent, x.parent.parent)
    end while
    return x
end function

Yolun yarılanması benzer şekilde çalışır ancak yalnızca diğer tüm ana işaretçilerin yerini alır:

function Find(x) is
    while x.parent ≠ x do
        x.parent := x.parent.parent
        x := x.parent
    end while
    return x
end function

İki kümeyi birleştirme

İşlem , x içeren kümeyi ve y içeren kümeyi birleşimleriyle değiştirir. ilk olarak x ve y içeren ağaçların köklerini belirlemek için kullanır . Kökler aynıysa yapacak bir şey yok. Aksi takdirde, iki ağaç birleştirilmelidir. Bu, ya üst işaretçiyi ayarlanarak yapılır x için y ya da üst işaretçiyi ayar y için x . Union(x, y)UnionFind

Hangi düğümün ebeveyn olacağı seçimi, ağaç üzerinde gelecekteki işlemlerin karmaşıklığı için sonuçlar doğurur. Dikkatsizce yapılırsa ağaçlar aşırı derecede uzayabilir. Örneğin, xUnion içeren ağacı her zaman y içeren ağacın bir alt ağacı yaptığını varsayalım . Öğelerle henüz başlatılmış bir ormanla başlayın ve , , ..., yürütün . Ortaya çıkan orman, kökü n olan tek bir ağaç içerir ve 1'den n'ye giden yol, ağaçtaki her düğümden geçer. Bu orman için çalışma zamanı olduğunu Ç ( n ) . ${\görüntüleme stili 1,2,3,\ldots ,n,}$Union(1, 2)Union(2, 3)Union(n - 1, n)Find(1)

Verimli bir uygulamada, ağaç yüksekliği, boyuta göre birleşim veya sıraya göre birleşim kullanılarak kontrol edilir . Bunların her ikisi de, bir düğümün yalnızca üst işaretçisinin yanı sıra bilgi depolamasını gerektirir. Bu bilgi, hangi kökün yeni ebeveyn olacağına karar vermek için kullanılır. Her iki strateji de ağaçların çok derinleşmemesini sağlar.

Boyuta göre birleşme durumunda, bir düğüm, yalnızca alt öğelerinin sayısı olan (düğümün kendisi dahil) boyutunu depolar. Kökleri x ve y olan ağaçlar birleştiğinde, daha çok nesli olan düğüm ebeveyn olur. İki düğüm aynı sayıda alt öğeye sahipse, bunlardan biri ebeveyn olabilir. Her iki durumda da, yeni üst düğümün boyutu, yeni toplam alt öğe sayısına ayarlanır.

function Union(x, y) is
    // Replace nodes by roots
    x := Find(x)
    y := Find(y)

    if x = y then
        return  // x and y are already in the same set
    end if

    // If necessary, rename variables to ensure that
    // x has at least as many descendants as y
    if x.size < y.size then
        (x, y) := (y, x)
    end if

    // Make x the new root
    y.parent := x
    // Update the size of x
    x.size := x.size + y.size
end function

Boyutu depolamak için gerekli bit sayısı açıkça n depolamak için gerekli bit sayısıdır . Bu, ormanın gerekli depolamasına sabit bir faktör ekler.

Dereceye göre birleşme için, bir düğüm , yüksekliği için bir üst sınır olan rütbesini saklar . Bir düğüm başlatıldığında, sırası sıfıra ayarlanır. Kökleri x ve y olan ağaçları birleştirmek için önce sıralarını karşılaştırın. Sıralar farklıysa, daha büyük sıra ağacı ebeveyn olur ve x ve y'nin sıraları değişmez. Dereceler aynıysa, ikisinden biri ebeveyn olabilir, ancak yeni ebeveynin sıralaması bir artırılır. Bir düğümün derecesi açıkça yüksekliğiyle ilişkiliyken, sıraları depolamak, yükseklikleri depolamaktan daha verimlidir. Bir düğümün yüksekliği bir Findişlem sırasında değişebilir , bu nedenle sıraları depolamak, yüksekliği doğru tutmak için fazladan çaba harcamaktan kaçınır. Sözde kodda, sıralamaya göre birleşim:

function Union(x, y) is
    // Replace nodes by roots
    x := Find(x)
    y := Find(y)

    if x = y then
        return  // x and y are already in the same set
    end if

    // If necessary, rename variables to ensure that
    // x has rank at least as large as that of y
    if x.rank < y.rank then
        (x, y) := (y, x)
    end if

    // Make x the new root
    y.parent := x
    // If necessary, increment the rank of x
    if x.rank = y.rank then
        x.rank := x.rank + 1
    end if
end function

Her düğümün rankı veya daha azı olduğu gösterilebilir . Sonuç olarak, sıra O (log log n ) bitlerinde saklanabilir , bu da onu ormanın boyutunun asimptotik olarak ihmal edilebilir bir kısmı yapar. ${\displaystyle \lfloor \lg n\rfloor }$

Yukarıdaki uygulamalardan, bir düğümün bir ağacın kökü olmadığı sürece, bir düğümün boyutunun ve sırasının önemli olmadığı açıktır. Bir düğüm bir kez alt öğe haline geldiğinde, boyutuna ve sıralamasına bir daha asla erişilmez.

Zaman karmaşıklığı

FindAna işaretçileri güncellemeyen ve Unionağaç yüksekliklerini kontrol etmeye çalışmayan ayrık kümeli bir orman uygulaması, O ( n ) yüksekliğinde ağaçlara sahip olabilir . Böyle bir durumda Findve Unionişlemleri O ( n ) zamanını gerektirir .

Bir uygulama tek başına yol sıkıştırmasını kullanıyorsa, n - 1'e kadar işlem ve f işlemin izlediği bir n MakeSet işlem dizisi, en kötü durum çalıştırma süresine sahiptir . Union Find${\displaystyle \Theta (n+f\cdot \sol(1+\log _{2+f/n}n\sağ))}$

Rütbe ile sendikayı kullanarak, fakat sırasında ebeveyn işaretçileri güncellemeden Find, çalışan bir zaman verir için m kadar, her türlü operasyonları n olmak üzere operasyonları. ${\displaystyle \Teta (m\log n)}$MakeSet

Boyutuna göre veya sıraya göre birliği ile yol sıkıştırma, bölme ya da ortadan bölünmüş, kombinasyonu için, çalışma süresini azaltır m kadar, herhangi bir tür işlemler n olmak üzere MakeSetiçin, operasyon . Bu , her işlemin itfa edilmiş çalışma süresini yapar . Bu asimptotik olarak en uygunudur, yani her ayrık küme veri yapısının işlem başına amorti edilmiş süre kullanması gerekir . Burada fonksiyonu olan ters Ackermann fonksiyonu . Ters Ackermann işlevi olağanüstü yavaş büyür, bu nedenle bu faktör, fiziksel evrende gerçekten yazılabilen herhangi bir n için 4 veya daha azdır . Bu, ayrık küme operasyonlarını pratik olarak sabit zamanla amorti eder. ${\görüntüleme stili \Teta (m\alfa (n))}$${\görüntüleme stili \Teta (\alfa (n))}$${\görüntüleme stili \Omega (\alfa (n))}$${\görüntüleme stili \alfa (n)}$

Union-Find'in O(log*(n)) zaman karmaşıklığının kanıtı

Ayrık kümeli bir ormanın performansının kesin analizi biraz karmaşıktır. Ancak, n nesne içeren ayrık kümeli bir ormandaki herhangi bir m Find veya Unionişlem için amorti edilen zamanın O (mlog ^* n ) olduğunu kanıtlayan çok daha basit bir analiz vardır ; burada log ^* yinelenen logaritmayı belirtir .

Önerme 1: Find işlevi köke giden yolu izlediğinden, karşılaştığı düğümün sırası artmaktadır.

Kanıt: Veri kümesine Bul ve Birleştir işlemleri uygulandığından, bu gerçeğin zaman içinde doğru olduğunu iddia edin. Başlangıçta, her düğüm kendi ağacının kökü olduğunda, bu önemsiz derecede doğrudur. Bir düğümün sıralamasının değiştirilebileceği tek durum, Sıralamaya Göre Birleştirme işleminin uygulanmasıdır. Bu durumda, daha küçük bir sıraya sahip bir ağaç, tersi yerine daha büyük bir sıraya sahip bir ağaca eklenecektir. Ve bulma işlemi sırasında, yol boyunca ziyaret edilen tüm düğümler, altlarından daha büyük bir sıraya sahip olan köke eklenecektir, bu nedenle bu işlem de bu gerçeği değiştirmeyecektir.

Önerme 2: R dereceli bir alt ağacın kökü olan bir u düğümünün en az düğümü vardır. ${\ Displaystyle 2^{r}}$

Kanıt: Başlangıçta her düğüm kendi ağacının kökü olduğunda, bu önemsiz derecede doğrudur. R dereceli bir u düğümünün en az 2 ^r düğümü olduğunu varsayalım . Daha sonra, r ranklı iki ağaç Union by Rank işlemi kullanılarak birleştirildiğinde , r + 1 sıralı bir ağaç ortaya çıkar ve kökünde en az düğüm bulunur.${\ Displaystyle 2^{r}+2^{r}=2^{r+1}}$

Önerme 3: R düzeyindeki maksimum düğüm sayısı en fazla${\displaystyle {\frac {n}{2^{r}}}.}$

Kanıt: Önlem 2'den , r dereceli bir alt ağacın kökü olan bir u düğümünün en az düğüme sahip olduğunu biliyoruz . Biz rütbe ait düğümlerin sayısını alacak r sıralaması ile her düğüm zaman r tam bir ağacın köküdür düğümlerin. Bu durumda, rütbe ve düğüm sayısı r olan${\ Displaystyle 2^{r}}$${\ Displaystyle 2^{r}}$${\displaystyle {\frac {n}{2^{r}}}.}$

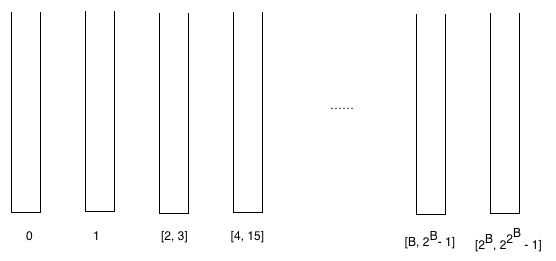
Kolaylık sağlamak için burada "kova" tanımlıyoruz: bir kova, belirli sıralara sahip köşeleri içeren bir kümedir.

Bazı kovalar oluşturuyoruz ve kovalara sıralarına göre endüktif olarak köşeler koyuyoruz. Yani, sıra 0'a sahip köşeler sıfırıncı kovaya, sıra 1'e sahip köşeler birinci kovaya, sıra 2 ve 3'e sahip köşeler ikinci kovaya gider. Eğer oda ^inci kova aralığından saflarıyla köşe içeriyor sonra (B + 1) St kepçe aralığından saflarıyla köşe içerir${\displaystyle \sol[r,2^{r}-1\sağ]=[r,R-1]}$${\displaystyle \sol[R,2^{R}-1\sağ].}$

Kovalar hakkında iki gözlem yapabiliriz.

1. Toplam kova sayısı en fazla log ^* n

   İspat: Bir kovadan diğerine gittiğimizde, güce bir iki daha ekleriz, yani bir sonraki kova olacak${\displaystyle \sol[B,2^{B}-1\sağ]}$${\displaystyle \sol[2^{B},2^{2^{B}}-1\sağ]}$

2. Kovadaki maksimum öğe sayısı en fazla${\displaystyle \sol[B,2^{B}-1\sağ]}$${\displaystyle {\frac {2n}{2^{B}}}}$

   Kanıt: Kovadaki maksimum öğe sayısı en fazla${\displaystyle \sol[B,2^{B}-1\sağ]}$${\displaystyle {\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}} }+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.}$

Let F işlemleri gerçekleştirilen "Bul" listesini temsil eder ve izin

O zaman m buluntuların toplam maliyeti${\displaystyle T=T_{1}+T_{2}+T_{3}.}$

Her bulma işlemi bir köke götüren tam olarak bir geçiş yaptığından, elimizde T ₁ = O ( m ) olur .

Ayrıca, yukarıdaki kova sayısı sınırından T ₂ = O ( m log ^* n ) elde ederiz .

İçin T ₃ , biz bir kenar geçme varsayalım u için v burada, u ve v kova dereceye sahip [ B , 2 ^B - 1] ve hacim aksi geçişi olur, bu değiştirme tertibatı zamanında kök (yok T _{1 '} de hesaba katılmalıdır ). Fix u ve diziyi düşünün rolünü almak v farklı bulmak operasyonlarında. Yol sıkıştırması nedeniyle ve bir kökün kenarını hesaba katmadığından, bu dizi yalnızca farklı düğümler içerir ve Lemma 1 nedeniyle, bu dizideki düğümlerin sıralarının kesinlikle arttığını biliyoruz. Kova olan düğümlerden derken uzunlukta olduğu sonucuna varabiliriz k sekansı (kaç kez düğüm arasında u aynı kova farklı köküne bağlı olan) kovalar içinde aşama sayısı en fazla olan B olduğu, en fazla${\displaystyle v_{1},v_{2},\ldots ,v_{k}}$${\ Displaystyle 2^{B}-1-B<2^{B}.}$

Öyleyse, ${\displaystyle T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.}$

Gözlem 1 ve 2'den şu sonuca varabiliriz:${\displaystyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$

Öyleyse, ${\displaystyle T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).}$

Uygulamalar

Ayrık-grubu veri yapıları modeli , bir dizi bölme , örneğin takip etmek için, bağlı bileşenlerin bir bölgesinin yönsüz grafik . Bu model daha sonra iki köşenin aynı bileşene ait olup olmadığını veya aralarına bir kenar eklenmesinin bir döngü ile sonuçlanıp sonuçlanmayacağını belirlemek için kullanılabilir. Union-Find algoritması, birleştirmenin yüksek performanslı uygulamalarında kullanılır .

Bu veri yapısı Boost Graph Library tarafından Artan Bağlı Bileşenler işlevini uygulamak için kullanılır . Ayrıca, bir grafiğin minimum yayılan ağacını bulmak için Kruskal'ın algoritmasının uygulanmasında önemli bir bileşendir .

Ayrık kümeli ormanlar olarak uygulamanın, yol sıkıştırması veya sıra buluşsal yöntemi olmasa bile kenarların silinmesine izin vermediğini unutmayın.

Sharir ve Agarwal, ayrık kümelerin en kötü durum davranışı ile Davenport-Schinzel dizilerinin uzunluğu arasındaki bağlantıları rapor ediyor , hesaplamalı geometriden bir kombinatoryal yapı.

Ayrıca bakınız

• Bölüm iyileştirme , ayrık kümeleri korumak için farklı bir veri yapısı, kümeleri birleştirmek yerine ayıran güncellemelerle
• Dinamik bağlantı

Referanslar

Dış bağlantılar

• Boost C++ kitaplıklarının bir parçası olan C++ uygulaması
• Görüntü segmentasyonunu renklendirmek için bir uygulama içeren bir Java uygulaması, İstatistiksel Bölge Birleştirme (SRM), IEEE Trans. Desen Anal. Mak. akıllı 26(11): 1452–1458 (2004)
• Java uygulaması: A Graphical Union–Find Uygulaması , Rory LP McGuire
• İzleyici Bileşen Kitaplığının parçası olan bir Matlab Uygulaması
• Python uygulaması
• Görsel açıklama ve C# kodu