Aristotelesçi gerçekçi matematik felsefesi - Aristotelian realist philosophy of mathematics
Gelen matematik felsefesi , Aristotelian gerçekçilik gibi matematik çalışmalar özellikleri bu tutan simetri , süreklilik ve sırayla anlamıyla fiziksel dünyada fark edilebilir (veya başka bir dünyada) olabilir. Sayılar gibi matematiğin nesnelerinin "soyut" bir dünyada var olmadığını, ancak fiziksel olarak gerçekleştirilebileceğini savunan Platonizm ile çelişir . Matematiğin yalnızca isimler veya çıkarım veya hesaplama yöntemleriyle değil, dünyanın belirli gerçek yönleriyle ilgili olduğunu kabul etmesiyle nominalizm ve kurgusalcılıkla çelişir .
Aristotelesçi realistler, felsefi olarak en önemli olarak saf matematikten ziyade uygulamalı matematiğe, özellikle matematiksel modellemeye vurgu yaparlar . Marc Lange , matematiksel gerçeklerin kendileri fiziksel dünya hakkında olduğu için, bilimde "Aristotelesçi gerçekçilik, matematiksel gerçeklerin belirgin bir şekilde matematiksel açıklamalarda açıklayıcı olmasına izin verdiğini" savunuyor. Paul Thagard , Aristotelesçi gerçekçiliği "zihinler ve bilim hakkında bilinenlere en iyi uyan mevcut matematik felsefesi" olarak tanımlar.
Tarih
Aristoteles matematik felsefesi üzerine kapsamlı bir şekilde yazmamış olsa da , konuyla ilgili çeşitli görüşleri, konunun hem soyutlamalar hakkında hem de gerçek uzay ve sayma dünyasına uygulanabilir olduğu konusunda tutarlı bir görüş sergilemektedir. On sekizinci yüzyıla kadar, en yaygın matematik felsefesi, niceliğin sürekli ( geometri ile incelenir ) ve ayrık (aritmetik ile çalışılır) olarak ikiye ayrıldığı " nicelik bilimi" olduğu şeklindeki Aristotelesçi görüştü .
Matematik felsefesine Aristotelesçi yaklaşımlar yirminci yüzyılda nadirdi, ancak Penelope Maddy tarafından Realism in Mathematics'te (1990) ve 2000'den beri James Franklin , Anne Newstead, Donald Gillies ve diğerleri gibi birkaç yazar tarafından yeniden canlandırıldı .
Sayılar ve kümeler
Aristotelesçi sayılara ( kardinal veya sayma) ilişkin görüşler, Aristoteles'in bir yığın veya koleksiyonun sayısının seçilen birime veya ölçüye göre olduğuna ilişkin gözlemiyle başlar: "'sayı' ölçülen bir çokluk ve bir ölçüler çokluğu anlamına gelir ... ölçü her zaman olmalıdır. ölçtüğü her şeye yüklenebilen özdeş bir şey olabilir, örneğin eğer şeyler atsa, ölçü 'at' olur." Glenn Kessler bunu, sayının bir yığın ile onu birimlere bölen bir evrensel arasındaki bir ilişki olduğu görüşünde geliştirir ; örneğin 4 sayısı bir papağan yığını ile yığını bu kadar çok papağana bölen evrensel "papağan olmak" arasındaki ilişkide gerçekleşir.
Aristotelesçi bir görüşe göre, oranlar kardinal sayılarla yakından bağlantılı değildir. Yükseklik gibi nicelikler arasındaki ilişkilerdir. İki yükseklik oranı, iki kütle veya iki zaman aralığı arasındaki ilişkiyle aynı olabilir.
Aristotelesçiler, sayıları olduğu kadar kümeleri de (Platoncu varlıklar olmaktan ziyade) fiziksel dünyada somutlaştırılmış olarak kabul ederler. Maddy, bir yumurta kartonu açıldığında, bir dizi üç yumurtanın algılandığını (yani, fiziksel dünyada gerçekleşen matematiksel bir varlık) savundu. Ancak tüm matematiksel söylemlerin gerçekçi bir şekilde yorumlanması gerekmez; örneğin Aristotelesçiler boş küme ve sıfırı kurgu ve muhtemelen daha yüksek sonsuzluklar olarak görebilirler.
Yapısal özellikler
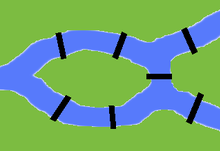
Aristotelesçiler simetri, süreklilik ve düzen gibi sayısal olmayan yapısal özellikleri sayılar kadar önemli görürler. Bu tür özellikler fiziksel gerçeklikte gerçekleşir ve matematiğin bazı bölümlerinin konusudur. Örneğin, grup teorisi farklı simetri türlerini sınıflandırırken, kalkülüs sürekli değişimi inceler. Bu tür yapılarla ilgili kanıtlanabilir sonuçlar doğrudan fiziksel gerçekliğe uygulanabilir. Örneğin Euler , Königsberg'in yedi köprüsünü bir kez ve bir kez yürümenin imkansız olduğunu kanıtladı .
epistemoloji
Matematiksel özellikler fiziksel dünyada gerçekleştiği için doğrudan algılanabilirler. Örneğin, insanlar yüz simetrisini kolayca algılarlar .
Aristotelesçiler ayrıca matematiksel düşüncede soyutlama ve idealleştirmeye de bir rol biçerler. Bu görüş, Aristoteles'in Fizik adlı eserinde , zihnin matematikte incelediği özellikleri, değişim dünyasından ayrı olarak cisimlerin zamansız özelliklerini göz önünde bulundurarak düşüncede 'ayırdığını' ifadesine kadar gider (Fizik II.2.193b31-35).
Matematiğin daha yüksek seviyelerinde, Aristotelesçiler Aristoteles'in Posterior Analytics teorisini takip ederler , buna göre matematiksel bir önermenin kanıtı ideal olarak okuyucunun önermenin neden doğru olması gerektiğini anlamasını sağlar.
Aristotelesçi gerçekçiliğe itirazlar
Aristotelesçi gerçekçilik için bir sorun , fiziksel dünyada gerçekleştirilemeyen veya gerçekleştirilemeyen daha yüksek sonsuzlukların ne şekilde açıklanacağıdır. Mark Balaguer yazıyor:
- "küme teorisi, tüm doğal sayılar kümesi gibi, bahçe çeşitliliği sonsuz kümelerini basitçe cüce edecek kadar büyük olan sonsuz kümelerin varlığına kendini adamıştır. Devasa sonsuz kümeler hakkındaki bu konuşmayı yaklaşık olarak yorumlamanın makul bir yolu yoktur. fiziksel objeler."
Aristotelesçiler, bilimlerin somutlaştırılmamış tümeller ile ilgilenebileceğini söylerler; örneğin renk bilimi, herhangi bir gerçek nesnede oluşmayan bir mavi tonuyla ilgilenebilir. Ancak bu, çoğu Aristotelesçi tarafından benimsenen ve tüm gerçek özelliklerin somutlaştırıldığını kabul eden somutlaştırma ilkesinin inkar edilmesini gerektirir . Temelinde örnekleme prensibi vermez matematik bir Aristotelian filozof Frege arasında bireyin ayrım anlamda referans olan Donald Gillies . Bu yaklaşımı, Aristotelesçi bir bakış açısından çok büyük transfinit kardinallerle başa çıkmak için bir yöntem geliştirmek için kullanmıştır .
Aristotelesçiliğe bir başka itiraz, matematiğin fiziksel dünyanın kendisiyle değil, fiziksel dünyanın idealleştirmeleriyle ilgilenmesidir . Aristoteles'in kendisi, geometrilerin mükemmel çemberleri incelediği, ancak gerçek dünyadaki çemberlerin mükemmel çemberler olmadığı argümanının farkındaydı, bu yüzden matematiğin fiziksel olmayan (Platonik) bir dünya üzerinde çalışıyor olması gerektiği anlaşılıyor. Aristotelesçiler, uygulamalı matematiğin idealleştirmeler yerine yaklaşıklıklar üzerinde çalıştığını ve bunun sonucunda modern matematiğin gerçek şeylerin karmaşık şekillerini ve diğer matematiksel yapılarını inceleyebileceğini yanıtlar .
Referanslar
bibliyografya
- John Bigelow, 1988, Sayıların Gerçekliği , Clarendon, Oxford, ISBN 9780198249573
- James Franklin, 2014, An Aristotelesçi Gerçekçi Matematik Felsefesi: Nicelik ve Yapı Bilimi Olarak Matematik , Palgrave Macmillan, Basingstoke, ISBN 9781137400727 .
- Keith Hossack, 2020, Bilgi ve Sayı Felsefesi: Sayılar Nedir ve Nasıl Bilinir , Bloomsbury, Londra, ISBN 9781350102927
- Andrew Irvine , 1990. Matematikte Fizikçilik , Dordrecht, Londra, ISBN 9780792305132
- Bob Knapp, 2014, Matematik Dünya Hakkında , Lexington KY, ISBN 9781500551971
- Penelope Maddy, 1990, Matematikte Gerçekçilik , Oxford University Press, New York, ISBN 9780198240358
- Woosuk Park, 2018, Felsefenin Matematiğe Mantığı Kaybı , Springer, Cham, ISBN 9783319951461