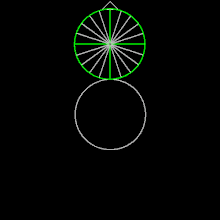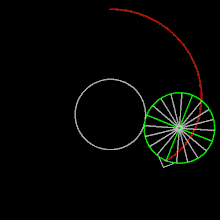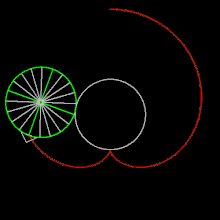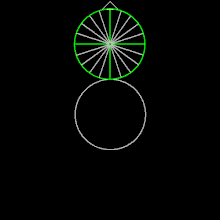
episikloid - Epicycloid

Kırmızı eğri, küçük daire (yarıçap r = 1) büyük dairenin (yarıçap R = 3) dış çevresinde dönerken izlenen bir episikloiddir .

İn geometrisi , bir koni a, düzlem eğri bir çemberi üzerindeki bir seçilmiş olan yerin izlediği yolu takip ederek üretilen çember bir -bunlara dış çember sabit bir daire çevresinde kaymadan -ki rulo. Özel bir rulet türüdür .

denklemler

Daha küçük dairenin yarıçapı r ve daha büyük dairenin yarıçapı R = kr ise , eğri için parametrik denklemler şu şekilde verilebilir:

${\displaystyle x(\theta )=(R+r)\cos \theta \ -r\cos \left({\frac {R+r}{r}}\theta \sağ)}$

${\displaystyle y(\theta )=(R+r)\sin \theta \ -r\sin \left({\frac {R+r}{r}}\theta \sağ),}$

veya:

${\displaystyle x(\theta )=r(k+1)\cos \theta -r\cos \sol((k+1)\theta \sağ)\,}$

${\displaystyle y(\theta )=r(k+1)\sin \theta -r\sin \sol((k+1)\theta \sağ).\,}$

(Başlangıç ​​noktasının daha büyük daire üzerinde olduğunu varsayarsak.)

Eğer k pozitif bir tamsayıdır, daha sonra eğri kapalı şekilde yapılmıştır ve k dişçiklidir (yani, keskin köşeler).

Eğer k bir rasyonel sayıysa , örneğin k = p / q'nun indirgenemez kesir olarak ifade edildiğini söyleyin , o zaman eğrinin p noktası vardır.

p ve q'yu görmek için animasyon dönüşlerini sayın.

Eğer k irrasyonel bir sayıysa , eğri asla kapanmaz ve daha büyük daire ile R + 2 r yarıçaplı bir daire arasındaki boşluğun yoğun bir alt kümesini oluşturur .

(x=0,y=0) orijinden ( küçük daire üzerindeki nokta) OP uzaklığı yukarı ve aşağı değişir. ${\görüntüleme stili p}$

R <= OP <= (R + 2r)

R = büyük dairenin yarıçapı ve

2r = küçük dairenin çapı

• Episikloid örnekler
• 

  k = 1 a kardioid

• 

  k = 2 bir nefroit

• 

  k = 3 - bir yoncaya benzer

• 

  k = 4 - bir dört yapraklıya benzer

• 

  k = 2,1 = 21/10

• 

  k = 3,8 = 19/5

• 

  k = 5.5 = 11/2

• 

  k = 7,2 = 36/5

Episikloid, özel bir epitrokoid türüdür .

Bir ucu olan bir episikl bir kardioid , iki ucu bir nefroittir .

Bir koni ve evolüt olan benzer .

Kanıt

kanıt için eskiz

Biz pozisyonu varsayalım , biz çözmek istiyoruz şeydir hareketli noktaya teğet noktasından radyan olduğunu ve teğet noktasına başlangıç noktasından radyan olduğunu. ${\görüntüleme stili p}$${\görüntüleme stili \alfa }$${\görüntüleme stili p}$${\görüntüleme stili\teta }$

İki döngü arasında kayma olmadığından, o zaman şuna sahibiz:

${\displaystyle \ell _{R}=\ell _{r}}$

Radyanın tanımına göre (yarıçap üzerindeki hız yayı), o zaman şuna sahibiz:

${\displaystyle \ell _{R}=\theta R,\ell _{r}=\alpha r}$

Bu iki koşuldan kimliği elde ederiz.

${\displaystyle \theta R=\alpha r}$

Hesaplayarak, ve arasındaki ilişkiyi elde ederiz , ki bu ${\görüntüleme stili \alfa }$${\görüntüleme stili\teta }$

${\displaystyle \alpha ={\frac {R}{r}}\theta}$

Şekilden, noktanın küçük daire üzerindeki konumunu net bir şekilde görüyoruz . ${\görüntüleme stili p}$

${\displaystyle x=\sol(R+r\sağ)\cos \teta -r\cos \sol(\teta +\alpha \sağ)=\sol(R+r\sağ)\cos \teta -r\ cos \sol({\frac {R+r}{r}}\theta \sağ)}$

${\displaystyle y=\sol(R+r\sağ)\sin \theta -r\sin \sol(\teta +\alpha \sağ)=\sol(R+r\sağ)\sin \theta -r\ sin \sol({\frac {R+r}{r}}\theta \sağ)}$

Ayrıca bakınız

MSWLogo'da ( Kardioid ) kaplumbağa ile animasyonlu gif

• Periyodik fonksiyonların listesi
• sikloid
• siklogon
• Deferent ve epicycle
• Episiklik dişli
• epitrokoid
• hiposikloid
• hipotrokoid
• Çoklu kardeş seti
• Rulet (eğri)
• Spirograf

Referanslar

• J. Dennis Lawrence (1972). Özel düzlem eğrilerinden oluşan bir katalog . Dover Yayınları. s.  161, 168-170, 175 . ISBN'si 978-0-486-60288-2.

Dış bağlantılar

• Weisstein, Eric W. "Episikloid" . Matematik Dünyası .
• Michael Ford tarafından " Episikloid ", Wolfram Gösteriler Projesi , 2007
• O'Connor, John J .; Robertson Edmund F. , "Episikloit" , Matematik MacTutor Tarih arşiv , University of St Andrews.
• Episikloidlerin, Perisikloidlerin ve Hiposikloidlerin Animasyonu
• Spirograf -- GeoFun
• Dişli Dişler formuna episikloid uygulamasına ilişkin tarihsel not