Cantor dağıtımı - Cantor distribution

kantor

Kümülatif dağılım fonksiyonu
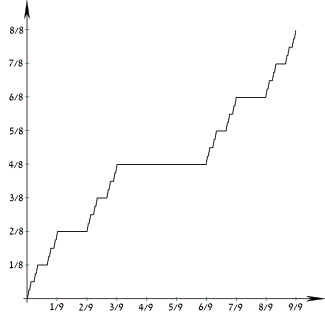
parametreler	Yok
Destek	kantor seti
PMF	Yok
CDF	cantor işlevi
Anlamına gelmek	1/2
Medyan	[1/3, 2/3] içinde herhangi bir yerde
mod	n/a
Varyans	1/8
çarpıklık	0
Örn. Basıklık	-8/5
MGF	${\displaystyle e^{t/2}\prod _{k=1}^{\infty }\cosh \left({\frac {t}{3^{k}}}\sağ)}$
CF	${\displaystyle e^{it/2}\prod _{k=1}^{\infty }\cos \left({\frac {t}{3^{k}}}\sağ)}$

Cantor dağılımı ise olasılık dağılımı olan kümülatif dağılım fonksiyonu olan Cantor işlevi .

Bu dağılımın ne olasılık yoğunluk fonksiyonu ne de olasılık kütle fonksiyonu vardır , çünkü kümülatif dağılım fonksiyonu sürekli bir fonksiyon olmasına rağmen, dağılım Lebesgue ölçüsüne göre mutlak olarak sürekli değildir ve nokta kütleleri de yoktur. Bu nedenle, ne kesikli ne de mutlak olarak sürekli bir olasılık dağılımıdır, ne de bunların bir karışımıdır. Aksine, tekil bir dağılım örneğidir .

Kümülatif dağılım işlevi her yerde süreklidir, ancak hemen hemen her yerde yataydır, bu nedenle bazen Şeytanın merdiveni olarak anılır , ancak bu terim daha genel bir anlama sahiptir.

karakterizasyon

Destek Cantor dağılımının olduğu Cantor kümesi kendisi (sayılabilir sonsuz sayıda) kümelerinin kesişimi:

${\displaystyle {\begin{aligned}C_{0}={}&[0,1]\\[8pt]C_{1}={}&[0,1/3]\cup [2/3,1 ]\\[8pt]C_{2}={}&[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9, 1]\\[8pt]C_{3}={}&[0,1/27]\cup [2/27,1/9]\cup [2/9,7/27]\cup [8/27] ,1/3]\cup \\[4pt]{}&[2/3,19/27]\cup [20/27,7/9]\cup [8/9,25/27]\cup [26 /27,1]\\[8pt]C_{4}={}&[0,1/81]\cup [2/81,1/27]\cup [2/27,7/81]\cup [ 8/81,1/9]\cup [2/9,19/81]\cup [20/81,7/27]\cup \\[4pt]&[8/27,25/81]\cup [ 26/81,1/3]\cup [2/3,55/81]\cup [56/81,19/27]\cup [20/27,61/81]\cup \\[4pt]&[ 62/81,21/27]\cup [8/9,73/81]\cup [74/81,25/27]\cup [26/27,79/81]\cup [80/81,1] \\[8pt]C_{5}={}&\cdots \end{hizalı}}}$

Cantor dağılımı, herhangi bir C _t ( t  ∈ { 0, 1, 2, 3, ... }) için, Cantor tarafından dağıtılmış rastgele değişkeni içeren C _t'deki belirli bir aralığın olasılığının aynı olduğu benzersiz olasılık dağılımıdır. 2 ^t aralığının her birinde 2 ^{- t} .

anlar

Bu dağılıma sahip bir rastgele değişken X için , beklenen değeri E( X ) = 1/2 olduğunu ve X'in tüm tek merkez momentlerinin 0 olduğunu simetri ile görmek kolaydır .

Toplam varyansın kanunu bulmak için kullanılabilir varyans var ( X ) olarak izler. Yukarıdaki grubu için C ₁ , izin Y = 0 ise X  ∈ [0,1 / 3] ve 1 ise X  ∈ [2 / 3,1]. Sonra:

${\displaystyle {\begin{hizalanmış}\operatöradı {var} (X)&=\operatöradı {E} (\operatöradı {var} (X\mid Y))+\operatöradı {var} (\operatöradı {E} ( X\mid Y))\\&={\frac {1}{9}}\operatöradı {var} (X)+\operatöradı {var} \left\{{\begin{matrix}1/6&{\mbox {olasılıkla}}\ 1/2\\5/6&{\mbox{olasılıkla}}\ 1/2\end{matris}}\sağ\}\\&={\frac {1}{9}} \operatöradı {var} (X)+{\frac {1}{9}}\end{hizalı}}}$

Bundan şunu elde ederiz:

${\displaystyle \operatöradı {var} (X)={\frac {1}{8}}.}$

Herhangi bir çift merkezi moment için kapalı biçimli bir ifade , önce çift kümülantlar elde edilerek bulunabilir.

${\displaystyle \kappa _{2n}={\frac {2^{2n-1}(2^{2n}-1)B_{2n}}{n\,(3^{2n}-1)}} ,\,\!}$

burada B _{2 , n} 2'dir , n inci Bernoulli sayısı ve kümülantların fonksiyonları olarak anlar eksprese .

Referanslar

daha fazla okuma

• Hewitt, E.; Stromberg, K. (1965). Gerçek ve Soyut Analiz . Berlin-Heidelberg-New York: Springer-Verlag. Bu, diğer standart metinlerde olduğu gibi, Cantor işlevine ve tek taraflı türevlerine sahiptir.
• Hu, Tian-Sen; Lau, Ka Sing (2002). "Sonsuzda Cantor Tipi Ölçülerin Fourier Asimptotikleri". Proc. AMS . 130 (9). s. 2711–2717. Bu, bu referans listesindeki diğer metinlerden daha moderndir.
• Knill, Ö. (2006). Olasılık Teorisi ve Stokastik Süreçler . Hindistan: Yurtdışı Basın.
• Mattilla, P. (1995). Öklid Uzaylarında Kümelerin Geometrisi . San Francisco: Cambridge University Press. Bu, fraktallar hakkında daha gelişmiş materyallere sahiptir.