Tetrasyon - Tetration

Gelen matematik , tetrasyon (ya da hiper-4 ) bir bir işlem göre Yinelemeli veya tekrar üs . Bu yanındadır hiperişlem sonra üs , ama daha önce Pentation . Kelime, Reuben Louis Goodstein tarafından tetra- (dört) ve yinelemeden türetilmiştir .

Tekrar üs Rudy Rücker gösterimi olarak tanıma göre vasıtasıyla , n- kopyaları bir sol sağdan üs ile tekrarlanır, üs Ie uygulama süreleri. n , fonksiyonun "yüksekliği" olarak adlandırılırken, a , üstelleştirmeye benzer şekilde "taban" olarak adlandırılır. Bu "olarak okunmalıdır olacağını n th tetrasyon bir ". ${\görüntüleme stili {^{n}a}}$${\displaystyle {a^{a^{\cdot ^{\cdot ^{a}}}}}}$${\görüntüleme stili n-1}$

Tetrasyon da özyinelemeli olarak tanımlanır

${\displaystyle {^{n}a}:={\begin{cases}1&{\text{if }}n=0\\a^{\left(^{(n-1)}a\sağ)} &{\text{if }}n>0\end{durumlar}}}$,

Tetrasyonu gerçek ve karmaşık sayılar gibi doğal olmayan sayılara genişletme girişimlerine izin verir.

Tetrasyonun iki tersi , n'inci kök ve logaritmik fonksiyonlara benzer şekilde süper kök ve süper logaritma olarak adlandırılır . Üç işlevden hiçbiri temel değildir .

Tetrasyon, çok büyük sayıların gösterimi için kullanılır .

Tanıtım

İlk dört hiperişlem burada gösterilmektedir ve tetrasyon serideki dördüncü işlem olarak kabul edilmektedir. Tekli işlem ardışık olarak tanımlanır , sıfırıncı işlem olarak kabul edilmektedir. ${\displaystyle a'=a+1}$

1. Ek

   ${\displaystyle a+n=a+\underbrace {1+1+\cdots +1} _{n}}$

   n, 1 kopyaları ilave bir .

2. Çarpma işlemi

   ${\displaystyle a\times n=\underbrace {a+a+\cdots +a} _{n}}$

   n, kopyaları bir eklenmesiyle birlikte.

3. üs alma

   ${\displaystyle a^{n}=\underbrace {a\times a\times \cdots \times a} _{n}}$

   n, kopyaları bir çarpma ile bir araya.

4. tetrasyon

   ${\displaystyle {^{n}a}=\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} _{n}}$

   n kopyaları bir üs tarafından kombine, sağdan sola.

Ardışıklık, ( a′ = a + 1) , en temel işlemdir; ek (iken bir + n ) o bir zincirleme ardışık olarak düşünülebilir doğal sayılar ilave edilmesi için bir birincil işlem, bir N ardılları bir ; Çarpma ( bir  x  , n doğal sayılar için benzer bir zincirleme bir ek içeren olarak düşünülebilir rağmen), aynı zamanda bir birinci operasyon , n sayısı , bir . Üs alma, n sayıda a içeren zincirleme bir çarpma ve n sayıda a içeren zincirleme bir kuvvet olarak tetratasyon ( ) olarak düşünülebilir . Yukarıdaki işlemlerin her biri bir öncekini yineleyerek tanımlanır; ancak, ondan önceki işlemlerden farklı olarak, tetratasyon temel bir fonksiyon değildir . ${\görüntüleme stili ^{n}bir\!}$

Parametre bir olarak adlandırılır baz parametresinin, n, şu şekilde de ifade edilebilir yükseklik . Tetrasyonun orijinal tanımında, yükseklik parametresi doğal bir sayı olmalıdır; örneğin, "üç kendi kendine beş kez eksi kaldırdı" veya "dört bir sürenin yarısına yükseldi" demek mantıksız olur. Bununla birlikte, toplama, çarpma ve üs almanın gerçek ve karmaşık sayılara uzantılara izin verecek şekilde tanımlanabilmesi gibi, tetratasyonu negatif sayılara, gerçek sayılara ve karmaşık sayılara genelleştirmek için çeşitli girişimlerde bulunulmuştur. Bunu yapmanın bir yolu, tetratasyon için özyinelemeli bir tanım kullanmaktır; herhangi bir pozitif gerçek ve negatif olmayan tamsayı için özyinelemeli olarak tanımlayabiliriz : ${\görüntüleme stili a>0}$ ${\görüntüleme stili n\geq 0}$${\ Displaystyle \,\!{^{n}a}}$

${\displaystyle {^{n}a}:={\begin{cases}1&{\text{if }}n=0\\a^{\left(^{(n-1)}a\sağ)} &{\text{if }}n>0\end{durumlar}}}$

Özyinelemeli tanım, doğal yükseklikler için tekrarlanan üstelleştirmeye eşdeğerdir ; ancak, bu tanım, , , gibi diğer yüksekliklere genişletmelere izin verir ve ayrıca bu uzantıların çoğu aktif araştırma alanlarıdır. ${\görüntüleme stili ^{0}a}$${\displaystyle ^{-1}a}$${\görüntüleme stili ^{i}a}$

terminoloji

Tetrasyon için birçok terim vardır ve bunların her birinin arkasında bir mantık vardır, ancak bazıları şu veya bu nedenle yaygın olarak kullanılmamıştır. Burada her bir terimin gerekçesi ve karşı mantığı ile bir karşılaştırması bulunmaktadır.

• Terimi tetrasyon yaptığı 1947 kağıtta Goodstein tarafından tanıtılan, Rekürsif Numarası Teorisinde ötesi, Sıra (kullanılan özyinelemeli baz temsilini genelleme Goodstein'e teoremi yüksek operasyonlarını kullanmak için), üstünlük kazanmıştır. Aynı zamanda popüler oldu Rudy Rucker 'ın Sonsuzluk ve Aklın .
• Terimi superexponentiation onun kağıt BRÖMER tarafından yayımlandı Superexponentiation Bu kitabında yüklemlik Aritmetik, Princeton University Press, 1986 yılında Ed Nelson daha önce kullanılmış 1987 yılında.
• Hipergüç terimi, tetratasyonu uygun bir şekilde tanımlayan hiper ve gücün doğal bir birleşimidir . Sorun , hiperişlem dizisine göre hiper anlamındadır . Hiperişlemler düşünüldüğünde, hiper terimi tüm dereceleri ifade eder ve süper terimi, derece 4 veya tetratasyonu ifade eder. Bu nedenle, bu düşünceler altında hipergüç yanıltıcıdır, çünkü yalnızca tetratasyona atıfta bulunur.
• Vadeli güç kulesi zaman zaman forma "düzen gücü kulesinde kullanılır n için" . Bununla birlikte, bu bir yanlış adlandırmadır, çünkü yinelenen bir üstel işlev olduğundan, tetratasyon yinelenen güç işlevleriyle (yukarıya bakın) ifade edilemez .${\ Displaystyle {\ \atop {\ }}{{\underbrace {a^{a^{\cdot ^{\cdot ^{a}}}}} } \atop n}}$

Kısmen bazı ortak terminoloji ve benzer simgesel sembolizm nedeniyle , tetratasyon genellikle yakından ilişkili işlevler ve ifadelerle karıştırılır. İşte birkaç ilgili terim:

Tetrasyon ile ilgili terimler

terminoloji	Biçim
tetrasyon	${\displaystyle a^{a^{\cdot ^{\cdot ^{a^{a}}}}}}$
yinelenen üsler	${\ Displaystyle a^{a^{\cdot ^{\cdot ^{a^{x}}}}}}$
İç içe üsteller (aynı zamanda kuleler)	${\displaystyle a_{1}^{a_{2}^{\cdot ^{\cdot ^{a_{n}}}}}}$
Sonsuz üsteller (aynı zamanda kuleler)	${\displaystyle a_{1}^{a_{2}^{a_{3}^{\cdot ^{\cdot ^{\cdot }}}}}}}$

İlk iki ifadelerde bir olan baz ve sayısı bir görünür olan yüksekliği için (eklenti bir x ). Üçüncü ifadede, n, bir yüksekliği , ancak tabanlarının her farklıdır.

Yinelenen üstellere atıfta bulunulurken dikkatli olunmalıdır, çünkü bu formun ifadelerine yinelenen üsler denir, bu belirsizdir, çünkü bu, yinelenen güçler veya yinelenen üsler anlamına gelebilir .

gösterim

Tetrasyon ifade etmek için kullanılabilecek birçok farklı notasyon stili vardır. Bazı gösterimler diğer hiper işlemleri tanımlamak için de kullanılabilir , bazıları ise tetratasyonla sınırlıdır ve hemen uzantısı yoktur.

Tetrasyon için gösterim stilleri

İsim	Biçim	Açıklama
Rudy Rucker gösterimi	${\displaystyle \,{}^{n}a}$	Maurer [1901] ve Goodstein [1947] tarafından kullanılmıştır; Rudy Rucker'ın kitabı Infinity and the Mind gösterimi popüler hale getirdi.
Knuth'un yukarı ok gösterimi	${\displaystyle a{\uparrow \uparrow }n}$	Daha fazla ok koyarak veya daha güçlü bir şekilde dizinlenmiş bir ok koyarak genişletmeye izin verir.
Conway zincirleme ok gösterimi	${\ Displaystyle a\rightarrow n\rightarrow 2}$	2 sayısını artırarak (yukarıdaki uzantılara eşdeğer) uzatmaya izin verir, aynı zamanda zinciri uzatarak daha da güçlü bir şekilde
Ackermann işlevi	${\displaystyle {}^{n}2=\operatör adı {A} (4,n-3)+3}$	Özel durumun Ackermann fonksiyonu cinsinden yazılmasına izin verir . ${\görüntüleme stili a=2}$
Yinelenen üstel gösterim	${\displaystyle \exp _{a}^{n}(1)}$	1 dışındaki ilk değerlerden yinelenen üstellere basit genişletmeye izin verir.
Hooshmand gösterimleri	${\displaystyle {\begin{hizalanmış}&\operatöradı {uxp} _{a}n\\[2pt]&a^{\frac {n}{}}\end{hizalı}}}$	MH Hooshmand [2006] tarafından kullanılmıştır.
Hiperoperasyon gösterimleri	${\displaystyle {\begin{hizalanmış}&a[4]n\\[2pt]&H_{4}(a,n)\end{hizalı}}}$	4 sayısını artırarak genişletmeye izin verir; bu, hiperoperasyon ailesini verir .
Çift şapka gösterimi	a^^n	Yukarı ok, şapka işaretiyle ( ^) aynı şekilde kullanıldığından , tetrasyon ( ^^); ASCII için uygun .

Yukarıdaki bir gösterimde yinelenen üstel gösterim kullanılır; bu genel olarak şu şekilde tanımlanır:

${\displaystyle \exp _{a}^{n}(x)=a^{a^{\cdot ^{\cdot ^{a^{x}}}}}}$ile n adet , bir s.

Yinelenen üsteller için çok fazla gösterim yoktur, ancak burada birkaç tane verilmiştir:

Yinelenen üsteller için gösterim stilleri

İsim	Biçim	Açıklama
Standart gösterim	${\displaystyle \exp _{a}^{n}(x)}$	Euler notasyonu icat etti ve yineleme notasyonu yaklaşık olarak uzun süredir var. ${\displaystyle \exp _{a}(x)=a^{x}}$${\görüntüleme stili f^{n}(x)}$
Knuth'un yukarı ok gösterimi	${\displaystyle (bir{\uparrow })^{n}(x)}$	Ok sayısını artırarak süper güçlere ve süper üstel işleve izin verir; büyük sayılarla ilgili makalede kullanılmıştır .
Metin gösterimi	exp_a^n(x)	Standart gösterime göre; ASCII için uygun .
J Gösterimi	x^^:(n-1)x	Üstelleştirmeyi tekrarlar. Bkz. J (programlama dili)

Örnekler

Tetrasyonun son derece hızlı büyümesi nedeniyle, aşağıdaki tablodaki değerlerin çoğu, bilimsel gösterimle yazılamayacak kadar büyüktür. Bu durumlarda, bunları taban 10'da ifade etmek için yinelenen üstel gösterim kullanılır. Ondalık nokta içeren değerler yaklaşık değerlerdir.

Tetrasyon örnekleri

${\görüntüleme stili x}$	${\görüntüleme stili {}^{2}x}$	${\görüntüleme stili {}^{3}x}$	${\görüntüleme stili {}^{4}x}$	${\görüntüleme stili {}^{5}x}$
1	1	1	1	1
2	4	16	65.536	2 65.536 veya (2.0035 × 10 19.728 )
3	27	7.625.597.484.987	${\displaystyle \exp _{10}^{3}(1.09902)}$(3.6 × 10 12 basamak)	${\displaystyle \exp _{10}^{4}(1.09902)}$
4	256	1.34078 × 10 154	${\displaystyle \exp _{10}^{3}(2.18726)}$(8.1 × 10 153 basamak)	${\displaystyle \exp _{10}^{4}(2.18726)}$
5	3.125	1.91101 × 10 2.184	${\displaystyle \exp _{10}^{3}(3.33928)}$(1.3 × 10 2.184 basamak)	${\displaystyle \exp _{10}^{4}(3.33928)}$
6	46.656	2.65912 × 10 36.305	${\displaystyle \exp _{10}^{3}(4.55997)}$(2.1 × 10 36.305 basamak)	${\displaystyle \exp _{10}^{4}(4.55997)}$
7	823,543	3.75982 × 10 695.974	${\displaystyle \exp _{10}^{3}(5.84259)}$(3.2 × 10 695.974 basamak)	${\displaystyle \exp _{10}^{4}(5.84259)}$
8	16.777.216	6.01452 × 10 15.151.335	${\displaystyle \exp _{10}^{3}(7.18045)}$(5.4 × 10 15.151.335 basamak)	${\displaystyle \exp _{10}^{4}(7.18045)}$
9	387.420.489	4.28125 × 10 369.693.099	${\displaystyle \exp _{10}^{3}(8.56784)}$(4.1 × 10 369.693.099 basamak)	${\displaystyle \exp _{10}^{4}(8.56784)}$
10	10.000.000.000	10 10.000.000.000	${\displaystyle \exp _{10}^{3}(10)}$(10 10.000.000.000 + 1 basamak)	${\displaystyle \exp _{10}^{4}(10)}$

Özellikler

Tetrasyon, üstelleştirmeye benzer çeşitli özelliklere ve ayrıca işleme özgü ve üstelleştirmeden kaybedilen veya kazanılan özelliklere sahiptir. Üs alma olmadığından gidip , ürün ve güç kuralları tetrasyon bir analog gerekmez; ifadeler ve çoğu durumda doğru değildir. ${\textstyle {}^{a}\sol({}^{b}x\sağ)=\sol({}^{ab}x\sağ)}$${\textstyle {}^{a}\sol(xy\sağ)={}^{a}x{}^{a}y}$

Bununla birlikte, tetratasyon farklı bir özelliği takip eder, ki . Bu gerçek en açık şekilde özyinelemeli tanım kullanılarak gösterilir. Bu özellikten, belirli denklemlerde b ve c arasında geçiş yapılmasına izin veren bir ispat izler . Kanıt şöyle devam ediyor: ${\textstyle {}^{a}x=x^{\sol({}^{a-1}x\sağ)}}$${\displaystyle \left({}^{b}a\sağ)^{\sol({}^{c}a\sağ)}=\sol({}^{c+1}a\sağ)^{ \left({}^{b-1}a\sağ)}}$

${\displaystyle {\begin{hizalı}&\sol({}^{b}a\sağ)^{\sol({}^{c}a\sağ)}\\={}&\sol(a^ {{}^{b-1}a}\sağ)^{\sol({}^{c}a\sağ)}\\={}&a^{\sol({}^{b-1}a \sağ)\sol({}^{c}a\sağ)}\\={}&a^{\left({}^{c}a\sağ)\sol({}^{b-1}a \right)}\\={}&\left({}^{c+1}a\sağ)^{\left({}^{b-1}a\sağ)}\end{hizalı}}}$

Bir x ve 10 sayısı asal olduğunda , herhangi bir m tamsayı için Euler teoremini kullanarak son m ondalık basamağını hesaplamak mümkündür . ${\görüntüleme stili \,\!\ ^{a}x}$

değerlendirme yönü

"Üs kulesi" olarak ifade edilen tetratasyonu değerlendirirken, seri üs ilk olarak en derin seviyede (gösterimde, tepe noktasında) yapılır. Örneğin:

${\displaystyle \,\!\ ^{4}2=2^{2^{2^{2}}}=2^{\left(2^{\left(2^{2}\right)}\ sağ)}=2^{\sol(2^{4}\sağ)}=2^{16}=65,\!536}$

Bu sıralama önemlidir çünkü üs alma ilişkisel değildir ve ifadeyi ters sırada değerlendirmek farklı bir cevaba yol açacaktır:

${\displaystyle \,\!2^{2^{2^{2}}}\neq \left({\left(2^{2}\right)}^{2}\sağ)^{2}= 4^{2\cdot 2}=256}$

Soldan sağa ifadeyi değerlendirmek daha az ilginç olarak kabul edilir; Soldan sağa değerlendirmesi yapabilmek, herhangi ifadesi olarak basitleştirilmiş olabilir . Bu nedenle kuleler sağdan sola (veya yukarıdan aşağıya) değerlendirilmelidir. Bilgisayar programcıları bu seçeneğe sağ çağrışımsal olarak atıfta bulunur . ${\görüntüleme stili ^{n}bir\!}$${\displaystyle a^{\sol(a^{n-1}\sağ)}\!\!}$

Uzantılar

Tetrasyon iki farklı şekilde genişletilebilir; denklemde , hem taban a hem de yükseklik n , tetratasyonun tanımı ve özellikleri kullanılarak genelleştirilebilir. Taban ve yükseklik, negatif olmayan tam sayıların ötesine, , gibi karmaşık fonksiyonlar ve sonsuz n yükseklikleri dahil olmak üzere farklı alanlara genişletilebilse de, tetratasyonun daha sınırlı özellikleri, tetraasyonu genişletme yeteneğini azaltır. ${\görüntüleme stili ^{n}bir\!}$${\görüntüleme stili {^{n}0}}$${\görüntüleme stili {}^{n}i}$

Bazlar için alan uzantısı

taban sıfır

Üstel tutarlı bir şekilde tanımlanmamıştır. Bu nedenle, tetratasyonlar daha önce verilen formülle açıkça tanımlanmamıştır. Ancak, iyi tanımlanmış ve var: ${\görüntüleme stili 0^{0}}$${\displaystyle \,{^{n}0}}$${\displaystyle \lim _{x\rightarrow 0}{}^{n}x}$

${\displaystyle \lim _{x\rightarrow 0}{}^{n}x={\begin{vakalar}1,&n{\metin{ çift}}\\0,&n{\metin{ tek}}\end {durumlar}}}$

Böylece tutarlı bir şekilde tanımlayabiliriz . Bu tanımlamaya benzer . ${\displaystyle {}^{n}0=\lim _{x\rightarrow 0}{}^{n}x}$${\displaystyle 0^{0}=1}$

Bu uzantı altında, , bu nedenle orijinal tanımdaki kural hala geçerlidir. ${\görüntüleme stili {}^{0}0=1}$${\görüntüleme stili {^{0}a}=1}$

Karmaşık bazlar

Yana karmaşık sayılar güçlere yükseltilebilir, tetrasyon uygulanabilir bazlar formu z = bir + çift (burada bir ve b gerçek). Örneğin, z = i ile ⁿ z'de , doğal logaritmanın ana dalı kullanılarak tetratasyon elde edilir ; Euler formülünü kullanarak şu ilişkiyi elde ederiz:

${\displaystyle i^{a+bi}=e^{{\frac {1}{2}}{\pi i}(a+bi)}=e^{-{\frac {1}{2}} {\pi b}}\left(\cos {\frac {\pi a}{2}}+i\sin {\frac {\pi a}{2}}\sağ)}$

Bu, herhangi bir ⁿ i = a + bi verildiğinde ^{n +1} i = a′ + b′i için özyinelemeli bir tanım önerir :

${\displaystyle {\begin{aligned}a'&=e^{-{\frac {1}{2}}{\pi b}}\cos {\frac {\pi a}{2}}\\[ 2pt]b'&=e^{-{\frac {1}{2}}{\pi b}}\sin {\frac {\pi a}{2}}\end{aligned}}}$

Aşağıdaki yaklaşık değerler türetilebilir:

Karmaşık bazların tetratasyonu değerleri

${\textstyle {}^{n}i}$	Yaklaşık değer
${\textstyle {}^{1}i=i}$	ben
${\textstyle {}^{2}i=i^{\sol({}^{1}i\sağ)}}$	0.2079
${\textstyle {}^{3}i=i^{\sol({}^{2}i\sağ)}}$	0.9472 + 0.3208 ben
${\textstyle {}^{4}i=i^{\sol({}^{3}i\sağ)}}$	0.0501 + 0.6021 ben
${\textstyle {}^{5}i=i^{\sol({}^{4}i\sağ)}}$	0.3872 + 0.0305 ben
${\textstyle {}^{6}i=i^{\sol({}^{5}i\sağ)}}$	0,7823 + 0,5446 ben
${\textstyle {}^{7}i=i^{\sol({}^{6}i\sağ)}}$	0.1426 + 0.4055 ben
${\textstyle {}^{8}i=i^{\sol({}^{7}i\sağ)}}$	0.5198 + 0.1184 ben
${\textstyle {}^{9}i=i^{\sol({}^{8}i\sağ)}}$	0,5686 + 0,6051 ben

Önceki bölümde olduğu gibi, ters bağıntının çözülmesi, beklenen ⁰ i = 1 ve ^-1 i = 0'ı verir ve n'nin negatif değerleri sanal eksende sonsuz sonuçlar verir. Karmaşık düzlemde çizilen dizinin tamamı , n'nin sonsuz olduğu değer olarak yorumlanabilecek olan 0,4383 + 0,3606 i sınırına spiraller çizer .

Bu tür tetrasyon dizileri Euler zamanından beri çalışılmıştır, ancak kaotik davranışlarından dolayı yeterince anlaşılmamışlardır. Tarihsel olarak yayınlanmış araştırmaların çoğu, sonsuz tekrarlanan üstel fonksiyonun yakınsamasına odaklanmıştır. Mevcut araştırmalar, fraktal ve sembolik matematik yazılımlarına sahip güçlü bilgisayarların ortaya çıkmasından büyük ölçüde yararlandı . Tetrasyon hakkında bilinenlerin çoğu, karmaşık dinamiklerin genel bilgisinden ve üstel haritanın özel araştırmalarından gelir.

Farklı yükseklikler için alan uzantıları

sonsuz yükseklikler

Tetrasyon sonsuz yüksekliklere kadar uzatılabilir ; yani, içindeki belirli a ve n değerleri için sonsuz bir n için iyi tanımlanmış bir sonuç vardır . Bunun nedeni, belirli bir aralıktaki bazlar için, yükseklik sonsuza doğru eğilim gösterdiğinden, tetratasyonun sonlu bir değere yakınsamasıdır . Örneğin, 2'ye yakınsar ve bu nedenle 2'ye eşit olduğu söylenebilir. 2'ye doğru olan eğilim, küçük bir sonlu kule değerlendirilerek görülebilir: ${\görüntüleme stili {}^{n}a}$${\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\cdot ^{\cdot ^{\cdot }}}}}}$

${\displaystyle {\begin{hizalanmış}{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2 }}^{1.414}}}}}&\yaklaşık {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.63 }}}}\\&\yaklaşık {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{1.76}}}\\&\yaklaşık {\sqrt {2 }}^{{\sqrt {2}}^{1.84}}\\&\yaklaşık {\sqrt {2}}^{1.89}\\&\yaklaşık 1.93\end{hizalı}}}$

Genel olarak, sonsuz üstel tekrarlanır sınırı olarak tanımlanan şekilde , n sonsuza gider için yakınsak e ^{- e} ≤ x ≤ e ^{1 / E} , yaklaşık 0.066 den 1,44 aralığı, ile gösterilen bir sonucu Leonard Euler . Varsa, limit, y = x ^y denkleminin pozitif bir gerçek çözümüdür . Böylece, x = y ^{1/ y} . Sonsuz üssünü tanımlayan sınırı x zaman mevcut değildir x > E ^{1 / E} maksimum nedeniyle y ^{1 / y} olan E ^{1 / E} . 0 < x < e ^{- e} olduğunda da sınır var ^olamaz . ${\displaystyle x^{x^{\cdot ^{\cdot ^{\cdot }}}}\!\!}$${\görüntüleme stili {}^{n}x}$

Bu, aşağıdaki tanımla karmaşık sayılar z'ye genişletilebilir :

${\displaystyle {}^{\infty }z=z^{z^{\cdot ^{\cdot ^{\cdot }}}}={\frac {\mathrm {W} (-\ln {z}) }{-\ln {z}}}~,}$

burada W , Lambert'in W fonksiyonunu temsil eder .

Sınırı olarak y = ^∞ x (pozitif gerçek hattında mevcut için, yani eğer E ^{- E} ≤ x ≤ E ^{1 / e} ) uygun olmalıdır x ^y = Y o bkz x ↦ Y = ^∞ X bir (düşük dal ) y ↦ x = y ^{1/ y'nin} ters fonksiyonu .

Negatif yükseklikler

Tetrasyon için özyinelemeli kuralı kullanabiliriz,

${\displaystyle {^{k+1}a}=a^{\sol({^{k}a}\sağ)},}$

kanıtlamak için : ${\ Displaystyle {}^{-1}a}$

${\displaystyle ^{k}a=\log _{a}\sol(^{k+1}a\sağ);}$

k yerine -1 koymak

${\displaystyle {}^{-1}a=\log _{a}\sol({}^{0}a\sağ)=\log _{a}1=0}$.

Daha küçük negatif değerler bu şekilde iyi tanımlanamaz. Aynı denklemde k yerine -2 koymak

${\displaystyle {}^{-2}a=\log _{a}\sol({}^{-1}a\sağ)=\log _{a}0=-\infty }$

hangi iyi tanımlanmamıştır. Bununla birlikte, bazen kümeler olarak kabul edilebilirler.

için herhangi bir tanım kuralla tutarlıdır çünkü ${\görüntüleme stili n=1}$${\görüntüleme stili \,\!{^{-1}1}}$

${\displaystyle {^{0}1}=1=1^{n}}$herhangi biri için .${\displaystyle \,\!n={^{-1}1}}$

Gerçek yükseklikler

Şu anda, tetraasyonun n'nin gerçek veya karmaşık değerlerine genişletilmesi genel sorununa genel olarak kabul edilen bir çözüm yoktur . Bununla birlikte, konuya yönelik birden fazla yaklaşım olmuştur ve farklı yaklaşımlar aşağıda özetlenmiştir.

Genelde, sorun buluyor - herhangi bir gerçek için a > 0 - Bir süper üstel fonksiyonu gerçek aşkın x > -2 o karşılar ${\displaystyle \,f(x)={}^{x}a}$

• ${\displaystyle \,{}^{-1}a=0}$
• ${\displaystyle \,{}^{0}a=1}$
• ${\displaystyle \,{}^{x}a=a^{\sol({}^{x-1}a\sağ)}}$tüm gerçek için ${\displaystyle x>-1.}$

Daha doğal bir uzantı bulmak için genellikle bir veya daha fazla ekstra gereksinim gereklidir. Bu genellikle aşağıdakilerin bir koleksiyonudur:

• Bir süreklilik gereksinimi (genellikle sadece bu , için her iki değişkende de süreklidir ).${\görüntüleme stili {}^{x}a}$${\görüntüleme stili x>0}$
• Bir türevlenebilirlik gereksinimi ( x cinsinden bir, iki, k kez veya sonsuz türevlenebilir olabilir ).
• Bir düzenlilik gereksinimi ( x içinde iki kez türevlenebilir anlamına gelir ):

${\displaystyle \left({\frac {d^{2}}{dx^{2}}}f(x)>0\sağ)}$ hepsi için ${\görüntüleme stili x>0}$

Dördüncü gereklilik yazardan yazara ve yaklaşımlar arasında farklılık gösterir. Tetrasyonun gerçek yüksekliklere genişletilmesi için iki ana yaklaşım vardır; biri düzenlilik gereksinimine, diğeri türevlenebilirlik gereksinimine dayanmaktadır . Bu iki yaklaşım, birbiriyle tutarsız sonuçlar ürettikleri için uzlaşılamayacak kadar farklı görünmektedir.

Bir uzunluktaki bir aralık için tanımlandığında, fonksiyonun tamamı tüm x > −2 için kolaylıkla takip eder . ${\displaystyle \,{}^{x}a}$

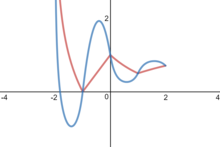
Gerçek yükseklikler için doğrusal yaklaşım

Bir doğrusal yaklaşım (süreklilik ihtiyacına bir çözüm, diferansiyellenebilirlik ihtiyacına yaklaştırma) ile verilir:

${\displaystyle {}^{x}a\yaklaşık {\başlangıç{durumlar}\log _{a}\sol(^{x+1}a\sağ)&x\leq -1\\1+x&-1< x\leq 0\\a^{\left(^{x-1}a\sağ)}&0<x\end{durumlar}}}$

buradan:

Doğrusal yaklaşım değerleri

yaklaşıklık	İhtisas
${\textstyle {}^{x}a\yaklaşık x+1}$	için -1 < x <0
${\textstyle {}^{x}a\yaklaşık bir^{x}}$	için 0 < x <1
${\textstyle {}^{x}a\yaklaşık bir^{a^{(x-1)}}}$	için 1 < X <2

ve bunun gibi. Ancak, yalnızca parçalı türevlenebilir; x'in tamsayı değerlerinde türev ile çarpılır . if ve sadece if için sürekli türevlenebilir . Örneğin, bu yöntemleri kullanmak ve${\görüntüleme stili \ln {a}}$${\ Displaystyle x>-2}$${\görüntüleme stili a=e}$${\displaystyle {}^{\frac {\pi }{2}}e\yaklaşık 5.868...}$${\ Displaystyle {}^{-4.3}0.5\yaklaşık 4.03335...}$

Hooshmand'ın makalesindeki bir ana teorem şöyle diyor: Let . Eğer sürekli ve tatmin koşulları geçerli: ${\displaystyle 0<a\neq 1}$${\displaystyle f:(-2,+\infty )\rightarrow \mathbb {R} }$

• ${\displaystyle f(x)=a^{f(x-1)}\;\;{\text{herkes için}}\;\;x>-1,\;f(0)=1,}$
• ${\görüntüleme stili f}$(-1, 0) üzerinde türevlenebilir ,
• ${\görüntüleme stili f^{\birincil }}$(-1, 0) üzerinde azalmayan veya artmayan bir fonksiyondur ,
• ${\displaystyle f^{\prime }\left(0^{+}\right)=(\ln a)f^{\prime }\left(0^{-}\right){\text{ veya }} f^{\prime }\sol(-1^{+}\sağ)=f^{\prime }\sol(0^{-}\sağ).}$

o zaman denklem yoluyla benzersiz bir şekilde belirlenir ${\görüntüleme stili f}$

${\displaystyle f(x)=\exp _{a}^{[x]}\left(a^{(x)}\sağ)=\exp _{a}^{[x+1]}(( x))\quad {\text{herkes için}}\;\;x>-2,}$

burada kesirli kısmını ifade eder , x ve bir - tekrarlanan fonksiyonu fonksiyonu . ${\görüntüleme stili (x)=x-[x]}$${\displaystyle \exp _{a}^{[x]}}$${\görüntüleme stili [x]}$${\displaystyle \exp _{a}}$

Kanıt, ikinci ila dördüncü koşulların önemsiz bir şekilde f'nin [-1, 0] üzerinde doğrusal bir fonksiyon olduğunu ima etmesidir .

Doğal tetratasyon fonksiyonuna doğrusal yaklaşım sürekli olarak türevlenebilir, ancak ikinci türevi argümanının tamsayı değerlerinde mevcut değildir. Hooshmand bunun için başka bir teklik teoremi türetmiştir: ${\ Displaystyle {}^{x}e}$

Aşağıdakileri karşılayan sürekli bir fonksiyon ise: ${\displaystyle f:(-2,+\infty )\rightarrow \mathbb {R} }$

• ${\displaystyle f(x)=e^{f(x-1)}\;\;{\text{herkes için}}\;\;x>-1,\;f(0)=1,}$
• ${\görüntüleme stili f}$(-1, 0) üzerinde dışbükeydir ,
• ${\displaystyle f^{\prime }\sol(0^{-}\sağ)\leq f^{\prime }\sol(0^{+}\sağ).}$

sonra . [ Doğal tetratasyon fonksiyonuna doğrusal yaklaşım için Hooshmand'ın adı burada .] ${\displaystyle f={\metin{uxp}}}$${\displaystyle f={\metin{uxp}}}$

Kanıt öncekiyle hemen hemen aynı; özyineleme denklemi bunu sağlar ve ardından dışbükeylik koşulu (-1, 0) üzerinde doğrusal olduğunu ima eder . ${\displaystyle f^{\prime }(-1^{+})=f^{\prime }(0^{+}),}$${\görüntüleme stili f}$

Bu nedenle, doğal tetrasyon doğrusal yaklaşım denkleminin tek çözüm ve olan dışbükey üzerinde (1, + ∞) . Yeterince türevlenebilir tüm diğer çözümler (-1, 0) aralığında bir bükülme noktasına sahip olmalıdır . ${\displaystyle f(x)=e^{f(x-1)}\;\;(x>-1)}$${\görüntüleme stili f(0)=1}$

Gerçek yükseklikler için daha yüksek dereceli yaklaşımlar

Doğrusal yaklaşımların ötesinde, ikinci dereceden bir yaklaşım (türevlenebilirlik gereksinimine göre) şu şekilde verilir:

${\displaystyle {}^{x}a\yaklaşık {\başlangıç{durumlar}\log _{a}\sol({}^{x+1}a\sağ)&x\leq -1\\1+{\ frac {2\ln(a)}{1\;+\;\ln(a)}}x-{\frac {1\;-\;\ln(a)}{1\;+\;\ln (a)}}x^{2}&-1<x\leq 0\\a^{\left({}^{x-1}a\sağ)}&x>0\end{durumlar}}}$

ki bu herkes için türevlenebilir , ancak iki kez türevlenebilir değil. Örneğin, Eğer bu doğrusal yaklaşık olarak aynıdır. ${\görüntüleme stili x>0}$${\displaystyle {}^{\frac {1}{2}}2\yaklaşık 1.45933...}$${\görüntüleme stili a=e}$

Hesaplanma şekli nedeniyle, üslerin aksine bu fonksiyon "iptal etmez" . Yani, ${\displaystyle \sol(a^{\frac {1}{n}}\sağ)^{n}=a}$

${\displaystyle {}^{n}\left({}^{\frac {1}{n}}a\sağ)=\underbrace {\sol({}^{\frac {1}{n}}a) \sağ)^{\sol({}^{\frac {1}{n}}a\sağ)^{\cdot ^{\cdot ^{\cdot ^{\cdot ^{\left({}^{ \frac {1}{n}}a\sağ)}}}}}}} _{n}\neq a}$.

İkinci dereceden bir yaklaşım olduğu gibi , çok daha hantal olsalar da, n dereceli yaklaşımlara genelleme yapmak için kübik yaklaşımlar ve yöntemler de mevcuttur.

Karmaşık yükseklikler

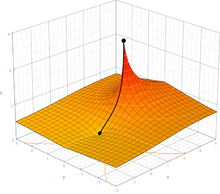
F ( z + 1) = exp( F ( z )) denkleminin bir çözümü olan ve F (0) = 1 ve F ( z ) ek koşullarını karşılayan benzersiz bir F fonksiyonunun olduğu artık kanıtlanmıştır. yaklaşımlar sabit noktalar logaritma (kabaca 0.318 ± 1.337 i gibi) z yaklaşımlar ± ı ∞ ve F olan holomorfik bütün karmaşık z gerçek eksenin bir kısmı dışında, -plane z ≤ -2 . Bu kanıt önceki bir varsayımı doğrular . Böyle bir fonksiyonun yapısı ilk olarak 1950'de Kneser tarafından gösterilmiştir. Bu fonksiyonun karmaşık haritası sağdaki şekilde gösterilmiştir. İspat , taban 'den büyük olduğu sürece, e'nin yanı sıra diğer tabanlar için de geçerlidir . Sonraki çalışmalar, inşaatı tüm karmaşık temellere genişletti. Bu işlevin karmaşık çift duyarlıklı yaklaşımı çevrimiçi olarak mevcuttur. ${\displaystyle e^{\frac {1}{e}}\yaklaşık 1.445}$

Tetrasyonun holomorfik olması şartı, benzersizliği açısından önemlidir. Birçok fonksiyon S şu şekilde oluşturulabilir:

${\displaystyle S(z)=F\!\left(~z~+\sum _{n=1}^{\infty }\sin(2\pi nz)~\alpha _{n}+\sum _ {n=1}^{\infty }{\Big (}1-\cos(2\pi nz){\Big )}~\beta _{n}\sağ)}$

burada α ve β , en azından Im  z'nin orta değerlerinde serinin yakınsamasını sağlamak için yeterince hızlı bozunan gerçek dizilerdir .

S fonksiyonu , S ( z + 1) = exp( S ( z )) , S (0) = 1 tetratasyon denklemlerini karşılar ve α _n ve β _n 0'a yeterince hızlı yaklaşırsa, pozitif komşulukta analitik olacaktır. gerçek eksen. Bununla birlikte, eğer { α } veya { β }'nın bazı elemanları sıfır değilse, o zaman sin ve cos'un sanal eksen boyunca üstel büyümesinden dolayı, S fonksiyonunun karmaşık düzlemde çok sayıda ek tekillikleri ve kesik çizgileri vardır; { α } ve { β } katsayıları ne kadar küçükse, bu tekillikler gerçek eksenden o kadar uzaktır.

Tetrasyonun karmaşık düzleme yayılması bu nedenle benzersizlik için esastır; Gerçek analitik tetrasyon özgü değildir.

Temel olmayan özyineleme

Tetrasyon ( kısıtlanmış ) temel özyinelemeli bir işlev değildir . Her temel özyinelemeli f fonksiyonu için , öyle bir c sabiti olduğu tümevarım yoluyla kanıtlanabilir . ${\displaystyle \mathbb {N} ^{2}}$

${\displaystyle f(x)\leq \underbrace {2^{2^{\cdot ^{\cdot ^{x}}}}} _{c}.}$

Sağ tarafı ile ifade ediyoruz . Tersine, tetratasyonun temel özyinelemeli olduğunu varsayalım. aynı zamanda temel özyinelemelidir. Yukarıdaki eşitsizliğe göre, öyle bir c sabiti vardır ki . İzin vererek , bir çelişkiye sahibiz . ${\görüntüleme stili g(c,x)}$${\displaystyle g(x,x)+1}$${\displaystyle g(x,x)+1\leq g(c,x)}$${\görüntüleme stili x=c}$${\displaystyle g(c,c)+1\leq g(c,c)}$

ters işlemler

Üs almanın iki ters işlemi vardır; kökler ve logaritmalar . Benzer şekilde, tetratasyonun tersleri genellikle süper kök ve süper logaritma olarak adlandırılır (Aslında, 3'ten büyük veya 3'e eşit tüm hiperişlemlerin benzer tersleri vardır); örneğin işlevinde , iki inversler küp süper kökü y ve süper logaritma tabanı  y ait x . ${\displaystyle {^{3}}y=x}$

süper kök

Süper kök tabana göre tetrasyon ters bir işlemdir: eğer , o zaman Y bir bir N inci süper kök x ( ya da ). ${\görüntüleme stili ^{n}y=x}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$${\displaystyle {\sqrt[{n}]{x}}_{4}}$

Örneğin,

${\displaystyle ^{4}2=2^{2^{2^{2}}}=65{,}536}$

yani 2, 65.536'nın 4. süper köküdür.

Kare süper kök

2.sıra süper kök , kare süper kök veya süper karekök iki eşdeğer gösterimler vardır ve . Lambert W fonksiyonunun tersidir ve bununla temsil edilebilir : ${\displaystyle \mathrm {ssrt} (x)}$${\displaystyle {\sqrt {x}}_{s}}$${\görüntüleme stili ^{2}x=x^{x}}$

${\displaystyle \mathrm {ssrt} (x)=e^{W(\ln x)}={\frac {\ln x}{W(\ln x)}}}$

Aşağıdaki denklem yalnızca şu durumlarda geçerli olduğundan, işlev aynı zamanda kök ve logaritma işlevlerinin yansıtıcı doğasını da gösterir : ${\displaystyle y=\mathrm {ssrt} (x)}$

${\displaystyle {\sqrt[{y}]{x}}=\log _{y}x}$

Gibi kare kökler , kare süper kök x tek çözüm olmayabilir. Kare köklerin aksine, x'in kare süperköklerinin sayısını belirlemek zor olabilir. Genel olarak, eğer , x'in 0 ile 1 arasında iki pozitif kare süper kökü vardır; ve ise , x'in 1'den büyük bir pozitif kare süperkökü vardır. x pozitifse ve 'den küçükse , herhangi bir gerçek kare süper kökü yoktur, ancak yukarıda verilen formül , herhangi bir sonlu x için sayısız sonsuz sayıda karmaşık olanı verir. 1'e eşit değil. İşlev, veri kümelerinin boyutunu belirlemek için kullanılmıştır . ${\displaystyle e^{-1/e}<x<1}$${\displaystyle x>1}$${\görüntüleme stili e^{-1/e}}$

Saat : ${\görüntüleme stili x=1}$

${\displaystyle \mathrm {ssqrt} (x)=1+(x-1)-(x-1)^{2}+{\frac {3}{2}}(x-1)^{3}- {\frac {17}{6}}(x-1)^{4}+{\frac {37}{6}}(x-1)^{5}-{\frac {1759}{120}} (x-1)^{6}+{\frac {13279}{360}}(x-1)^{7}+\mathrm {O} \left((x-1)^{8}\sağ) }$

Diğer süper kökler

Her bir tam sayı için n > 2 , fonksiyon ^{, n} x tanımlanır ve artan x ≥ 1 ve ^n, 1 = 1 böylece, N inci süper kök x , için mevcuttur, x ≥ 1 . ${\displaystyle {\sqrt[{n}]{x}}_{s}}$

Üçüncü dereceden bir süper kök için daha basit ve daha hızlı formüllerden biri, özyinelemeli formüldür, eğer: "x ^ x ^ x = a" ve sonraki x (n + 1) = exp (W (W (x (n) ) * ln (a)))) örneğin x (0) = 1.

Ancak, yukarıdaki doğrusal yaklaşım kullanılırsa, o zaman -1 < y ≤ 0 ise , var olamaz. ${\displaystyle ^{y}x=y+1}$${\displaystyle ^{y}{\sqrt {y+1}}_{s}}$

Kare süper kök ile aynı şekilde, diğer süper kökler için terminoloji normal köklere dayandırılabilir : "küp süper kökler" şu şekilde ifade edilebilir ; "4. süper kök" şu şekilde ifade edilebilir ; ve " n inci süper kök" dir . Not birden fazla olabileceğinden benzersiz, tanımlanmamış olabilir , n ^inci kökü. Örneğin, x tek (gerçek) süper kök eğer sahiptir n olan garip ve yukarı ikiye eğer n olduğunu bile . ${\displaystyle {\sqrt[{3}]{x}}_{s}}$${\displaystyle {\sqrt[{4}]{x}}_{s}}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$${\displaystyle {\sqrt[{n}]{x}}_{s}}$

Tetrasyonun sonsuz yüksekliklere uzatılmasında olduğu gibi, süper kök n = ∞'ye kadar genişletilebilir , eğer 1/ e ≤ x ≤ e ise iyi tanımlanır . Bunu ve dolayısıyla şunu not edin . Bu nedenle, iyi tanımlandığında ve normal tetraasyonun aksine, temel bir fonksiyondur . Örneğin, . ${\displaystyle x={^{\infty }y}=y^{\sol[^{\infty }y\sağ]}=y^{x},}$${\görüntüleme stili y=x^{1/x}}$${\displaystyle {\sqrt[{\infty }]{x}}_{s}=x^{1/x}}$${\displaystyle {\sqrt[{\infty }]{2}}_{s}=2^{1/2}={\sqrt {2}}}$

Bu izler Gelfond-Schneider teoremi süper kök olduğu herhangi bir pozitif tamsayı için n ya tamsayı ya da transandantal ve tamsayı ve mantıksız olduğunu. İkinci durumda irrasyonel süper köklerin aşkın olup olmadığı hala açık bir sorudur. ${\displaystyle {\sqrt {n}}_{s}}$${\displaystyle {\sqrt[{3}]{n}}_{s}}$

süper logaritma

Tetrasyonun sürekli artan ( x cinsinden ) tanımı, ^x a , seçildiğinde, karşılık gelen süper logaritma veya tüm x gerçek sayıları ve a > 1 için tanımlanır . ${\displaystyle \operatör adı {slog} _{a}x}$${\displaystyle \log _{a}^{4}x}$

slog _a  x işlevi şunları karşılar:

${\displaystyle {\begin{array}{lcl}\operatorname {slog} _{a}{^{x}a}&=&x\\\operatorname {slog} _{a}a^{x}&=&1+ \operatöradı {slog} _{a}x\\\operatöradı {slog} _{a}x&=&1+\operatöradı {slog} _{a}\log _{a}x\\\operatöradı {slog} _{a }x&>&-2\end{dizi}}}$

Açık sorular

Tetrasyonun uzantılarıyla ilgili problemlerin dışında, özellikle tamsayılar ve irrasyonel sayılar gibi sayı sistemleri arasındaki ilişkiler söz konusu olduğunda, tetratasyonla ilgili birkaç açık soru vardır :

• Pozitif bir tam sayı olup olmadığı bilinmemektedir n olan ^n- tt veya ⁿ e bir tam sayı olduğu. Özellikle, ister ya bilinmemektedir ⁴ tt veya ⁵ e bir tam sayı olduğu.
• ⁿ q herhangi bir pozitif tamsayı n ve pozitif tamsayı olmayan rasyonel q için bir tam sayı olup olmadığı bilinmemektedir . Örneğin, ⁴ x = 2 denkleminin pozitif kökünün bir rasyonel sayı olup olmadığı bilinmemektedir .

Ayrıca bakınız

• Ackermann işlevi
• Büyük O gösterimi
• Çift üstel fonksiyon
• hiperoperasyon
• yinelenen logaritma
• Simetrik seviye indeksi aritmetiği

Notlar

Referanslar

• Daniel Geisler, Tetrasyon
• Ioannis Galidakis , hyper4'ü tamsayı olmayanlara genişletme hakkında (tarihsiz, 2006 veya öncesi) (Bir sonraki referansın daha basit, okunması daha kolay bir incelemesi)
• Ioannis Galidakis , On Extending hyper4 ve Knuth's Up-Arrow Notation to the Reals (tarihsiz, 2006 veya öncesi).
• Robert Munafo, hyper4 işlevinin gerçeklere genişletilmesi ( Tetrasyonun gerçek sayılara genişletilmesi hakkında resmi olmayan bir tartışma.)
• Lode Vandevenne, İkinin Karekökünün Tetrasyonu . (2004). (Tetrasyonu gerçek sayılara genişletmeye çalışın.)
• Ioannis Galidakis, Matematik , (Tetrasyon araştırmalarına ilişkin kesin referans listesi. Lambert W fonksiyonu, Riemann yüzeyleri ve analitik devam hakkında çok fazla bilgi.)
• Joseph MacDonell, Hipergüç Fonksiyonunun Bazı Kritik Noktaları .
• Dave L. Renfro, sonsuz yinelenen üstellere yönelik Web sayfaları
• Knobel, R. (1981). "Üsseller Tekrar Edildi". Amerikan Matematiksel Aylık . 88 (4): 235–252. doi : 10.1080/00029890.1981.11995239 .
• Hans Maurer, "Über die Funktion für ganzzahliges Argümanı (Abundanzen)." Mittheilungen der Mathematische Gesellschaft, Hamburg 4 , (1901), s. 33-50. ( Knobel'in makalesinden kullanımına referans .)${\displaystyle y=x^{[x^{[x(\cdots )]}]}}$ ${\displaystyle \ {^{n}a}}$
• Dördüncü Operasyon
• Luca Moroni, Sonsuz güç kulesinin tuhaf özellikleri ( https://arxiv.org/abs/1908.05559 )

daha fazla okuma

• Galidakis, Ioannis; Weisstein, Eric Wolfgang . "Güç Kulesi" . Matematik Dünyası . 2019-07-05 alındı .