Matematiksel tümevarım - Mathematical induction

Matematiksel indüksiyon a, matematiksel kanıt tekniği. Esasen, bir P ( n ) ifadesinin her n  = 0, 1, 2, 3, doğal sayı için geçerli olduğunu kanıtlamak için kullanılır . . . ; yani, genel ifade sonsuz sayıda P (0), P (1), P (2), P (3), . . . . Domino taşları düşmek veya merdivene tırmanmak gibi resmi olmayan metaforlar bu tekniği açıklamaya yardımcı olur:

Matematiksel tümevarım, bir merdivende istediğimiz kadar yükseğe tırmanabileceğimizi, alt basamağa ( temel ) tırmanabileceğimizi ve her basamaktan bir sonrakine ( adım ) tırmanabileceğimizi kanıtlayarak ispatlar .

—  Somut Matematik , sayfa 3 kenar boşlukları.

Bir endüksiyon ile dayanıklı iki durumda oluşur. İlki, temel durum (veya temel ), diğer durumlar hakkında herhangi bir bilgi varsaymadan n = 0 için ifadeyi kanıtlar . İkinci vaka, indüksiyon adım , kanıtlıyor eğer deyim verilmiş herhangi bir durum için de geçerlidir n = k , o zaman o da bir sonraki durum için tutmak zorundadır  n = k + 1 Bu iki adım deyimi her doğal sayı için tutan kurmak n . Temel durum mutlaka n = 0 ile başlamaz , ancak genellikle n = 1 ile ve muhtemelen herhangi bir sabit doğal sayı n = N ile başlar ve tüm n ≥ N doğal sayıları için ifadenin doğruluğunu ortaya koyar .

Yöntem, ağaçlar gibi daha genel sağlam temelli yapılar hakkındaki ifadeleri kanıtlamak için genişletilebilir ; olarak bilinen bu genelleme, yapısal indüksiyonu , kullanılan matematiksel mantık ve bilgisayar biliminin . Bu genişletilmiş anlamda matematiksel tümevarım özyineleme ile yakından ilişkilidir . Matematiksel tümevarım, biçimsel ispatlarda kullanılan bir çıkarım kuralıdır ve bilgisayar programları için çoğu doğruluk ispatının temelidir .

Adı aksini düşündürse de, matematiksel tümevarım , felsefede kullanıldığı şekliyle tümevarımsal akıl yürütme ile karıştırılmamalıdır (bkz . Tümevarım Problemi ). Matematiksel yöntem, genel bir ifadeyi kanıtlamak için sonsuz sayıda durumu inceler, ancak bunu , sonsuz sayıda değer alabilen n değişkenini içeren sonlu bir tümdengelimli akıl yürütme zinciriyle yapar .

Tarih

370 M.Ö. Platon 'ın Parmenides örtük bir endüktif ispat erken örneğini içeriyor olabilir. Ters bir yinelenen teknik, yukarı yerine geri sayma , sorites paradoksunda bulunur ; burada 1.000.000 kum tanesi bir yığın oluşturursa ve bir yığından bir kum tanesi onu bir yığın bırakırsa, o zaman tek bir kum tanesi kalır. (hatta hiç tahıl) bir yığın oluşturur.

Hindistan'da, erken matematiksel tümevarım yoluyla örtülü ispatlar görünür Bhaskara 'ın ' döngüsel yöntemle ' ve de el-Fakhri tarafından yazılan El-Kerecî için uygulamasıyla MS 1000 civarında, aritmetik diziler kanıtlamak için binom teoremini ve özelliklerini Pascal üçgeni .

Bununla birlikte, bu eski matematikçilerin hiçbiri tümevarım hipotezini açıkça belirtmedi. Bir başka benzer dava (Freudenthal dikkatle gösteriyordu Vacca, yazmıştır aksine) o oldu Francesco Maurolico onun içinde Arithmeticorum libri ikilisi birinci toplamı olduğunu kanıtlamak için tekniğini kullanıldı (1575), n tek tamsayı olduğu n ² .

Tümevarımın ilk titiz kullanımı Gersonides (1288-1344) tarafından yapılmıştır . İndüksiyon ilkesi ilk açık bir şekilde formüle göre verilen Pascal onun içinde Traité du üçgen arithmétique (1665). Başka bir Fransız, Fermat , ilgili bir ilkeden bol bol yararlandı: sonsuz inişle dolaylı kanıt .

Tümevarım hipotezi İsviçreli Jakob Bernoulli tarafından da kullanıldı ve o andan itibaren iyi bilinir hale geldi. İlkenin modern resmi muamelesi, George Boole , Augustus de Morgan , Charles Sanders Peirce , Giuseppe Peano ve Richard Dedekind ile ancak 19. yüzyılda geldi .

Açıklama

Matematiksel indüksiyon çıkarır en basit ve en yaygın şekli, bir ilgili bir açıklama bu doğal sayı , n (olduğundan, bir tam sayıdır , n ≥ 0 veya 1) tüm değerleri için tutan n . Kanıt iki adımdan oluşur:

1. Başlangıç veya temel durum : ifadesi 0, ya da 1 için de geçerlidir olduğunu kanıtlamaktadır.
2. İndüksiyon adım , endüktif adım veya adım vaka : Her için kanıtlamak n ifadesi için dayanırsa, n o zaman için de geçerlidir, n + 1'e . Başka bir deyişle, ifadenin rastgele bir doğal sayı n için geçerli olduğunu varsayalım ve ifadenin n + 1 için geçerli olduğunu kanıtlayın .

Tümevarım adımındaki, ifadenin belirli bir n için geçerli olduğu hipotezine , tümevarım hipotezi veya tümevarım hipotezi denir . Endüktif adımı kanıtlamak için, n için tümevarım hipotezi varsayılır ve ardından bu varsayım, ifadenin n + 1 için geçerli olduğunu kanıtlamak için kullanılır .

Doğal sayıları 0'dan başlayacak şekilde tanımlamayı tercih eden yazarlar, temel durumda bu değeri kullanır; doğal sayıları 1'den başlayacak şekilde tanımlayanlar bu değeri kullanır.

Örnekler

Ardışık doğal sayıların toplamı

Tüm doğal sayılar n için aşağıdaki P ( n ) ifadesini kanıtlamak için matematiksel tümevarım kullanılabilir .

${\displaystyle P(n)\!:\ \ 0+1+2+\cdots +n\,=\,{\frac {n(n+1)}{2}}.}$

Bu, belirli bir sayıdan küçük veya ona eşit doğal sayıların toplamı için genel bir formül belirtir; aslında sonsuz bir ifade dizisi: , , , vb. ${\displaystyle 0={\tfrac {(0)(0+1)}{2}}}$${\displaystyle 0+1={\tfrac {(1)(1+1)}{2}}}$${\displaystyle 0+1+2={\tfrac {(2)(2+1)}{2}}}$

teklif. herhangi biri için, ${\displaystyle n\in \mathbb {N} }$${\displaystyle 0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.}$

Kanıt. Let P ( n ) deyimi Biz üzerinde indüksiyonla bir kanıt vermek n . ${\displaystyle 0+1+2+\cdots +n={\tfrac {n(n+1)}{2}}.}$

Temel durum : İfadenin en küçük doğal sayı n = 0için geçerli olduğunu gösterin.

P (0) açıkça doğrudur: ${\displaystyle 0={\tfrac {0(0+1)}{2}}\,.}$

Endüktif adım : Herhangi bir k ≥ 0 için, P ( k )geçerliyse, P ( k +1)'nin de geçerliolduğunu gösterin.

Belirli bir k için , n = k tek durumunun geçerli olduğu, yani P ( k )'nin doğru olduğu tümevarım hipotezini varsayalım :

${\displaystyle 0+1+\cdots +k\ =\ {\frac {k(k{+}1)}{2}}.}$

Bunu takip eder:

${\displaystyle (0+1+2+\cdots +k)+(k{+}1)\ =\ {\frac {k(k{+}1)}{2}}+(k{+}1 ).}$

Cebirsel olarak, sağ taraf şu şekilde sadeleşir:

${\displaystyle {\begin{hizalanmış}{\frac {k(k{+}1)}{2}}+(k{+}1)&\ =\ {\frac {k(k{+}1) +2(k{+}1)}{2}}\\&\ =\ {\frac {(k{+}1)(k{+}2)}{2}}\\&\ =\ { \frac {(k{+}1)((k{+}1)+1)}{2}}.\end{hizalı}}}$

Aşırı sol ve sağ tarafları eşitleyerek şunu çıkarıyoruz:

${\displaystyle 0+1+2+\cdots +k+(k{+}1)\ =\ {\frac {(k{+}1)((k{+}1)+1)}{2}} .}$

Yani, P ( k+ 1) ifadesi de tümevarım adımını belirleyerek geçerlidir.

Sonuç : Hem temel durum hem de tümevarım adımının doğru olduğu kanıtlandığından, matematiksel tümevarımla P ( n )ifadesiher n doğal sayısı için geçerlidir. ∎

trigonometrik eşitsizlik

Tümevarım genellikle eşitsizlikleri kanıtlamak için kullanılır. Örnek olarak, bunu herhangi bir gerçek sayı ve doğal sayı için kanıtlıyoruz . ${\displaystyle |\!\sin nx|\leq n|\!\sin x|}$${\görüntüleme stili x}$${\görüntüleme stili n}$

İlk bakışta, herhangi bir gerçek sayı için daha genel bir versiyonun tümevarım olmadan kanıtlanabileceği görünebilir ; ancak durum , tamsayı olmayan değerler için yanlış olabileceğini gösterir . Bu, ifadeyi özellikle doğal değerleri için incelememizi önerir ve tümevarım en hazır araçtır. ${\displaystyle |\!\sin nx|\leq n\,|\!\sin x|}$${\görüntüleme stili n,x}$${\textstyle n={\frac {1}{2}},\,x=\pi }$${\görüntüleme stili n}$${\görüntüleme stili n}$

teklif . Herhangi biri için, . ${\displaystyle x\in \mathbb {R} ,n\in \mathbb {N} }$${\displaystyle |\!\sin nx|\leq n\,|\!\sin x|}$

Kanıt. Keyfi bir gerçek sayı Fix ve izin deyim olmak . giriş yapıyoruz . ${\görüntüleme stili x}$${\görüntüleme stili P(n)}$${\displaystyle |\!\sin nx|\leq n\,|\!\sin x|}$${\görüntüleme stili n}$

Temel durum: Hesaplamadoğrular. ${\displaystyle |\!\sin 0x|=0\leq 0=0\,|\!\sin x|}$${\görüntüleme stili P(0)}$

Tümevarım adımı: Herhangi bir doğal sayınınanlamını gösteriyoruz. Tümevarım hipotezini varsayın: belirli bir değeriçin tek durumdoğrudur. Açı toplama formülünü ve üçgen eşitsizliğini kullanarak şunuçıkarabiliriz: ${\displaystyle P(k)\P(k{+}1)} anlamına gelir$${\görüntüleme stili k}$${\görüntüleme stili n=k\geq 0}$${\görüntüleme stili P(k)}$

${\displaystyle {\begin{array}{rcll}|\sin(k{+}1)x|&=&|\sin kx\,\cos x+\sin x\,\cos kx\,|&{\ text{(açı toplama)}}\\&\leq &|\!\sin kx\,\cos x|+|\!\sin x\,\cos kx|&{\text{(üçgen eşitsizliği)}} \\&=&|\!\sin kx|\,|\!\cos x|+|\!\sin x|\,|\!\cos kx|&\\&\leq &|\!\sin kx|+|\!\sin x|&(\,|\!\cos t|\leq 1)\\&\leq &k\,|\!\sin x|+|\!\sin x|&{ \text{(tümevarım hipotezi}})\\&\ =\ &(k{+}1)\,|\!\sin x|.&\end{dizi}}}$

Aşırı sol ve sağ miktarlar arasındaki eşitsizlik , tümevarım adımını tamamlayan bunun doğru olduğunu gösterir . ${\ Displaystyle P(k{+}1)}$

Sonuç : Bu önermetüm doğal sayılar için geçerlidir. ∎ ${\görüntüleme stili P(n)}$${\görüntüleme stili n}$

Varyantlar

Uygulamada, tümevarım yoluyla ispatlar, ispatlanacak özelliğin tam doğasına bağlı olarak genellikle farklı şekilde yapılandırılır. Tüm tümevarım çeşitleri, sonlu ötesi tümevarımın özel durumlarıdır; aşağıya bakın .

0 veya 1 dışında indüksiyon temeli

Bir önermeyi tüm doğal sayılar için değil, yalnızca belirli bir b sayısından büyük veya ona eşit tüm n sayıları için kanıtlamak istersek, tümevarımla kanıt aşağıdakilerden oluşur:

1. İfadenin n = b olduğunda geçerli olduğunu gösterme .
2. İfadenin keyfi bir n ≥ b sayısı için geçerli olması durumunda, aynı ifadenin n + 1 için de geçerli olduğunu göstermek .

Bu, örneğin, n ≥ 3 için 2 ⁿ ≥ n + 5 olduğunu göstermek için kullanılabilir .

Bu şekilde, bir P ( n ) ifadesinin tüm n ≥ 1 için , hatta tüm n ≥ -5 için geçerli olduğu kanıtlanabilir . Bu matematiksel tümevarım biçimi aslında önceki formun özel bir halidir, çünkü ispatlanacak ifade P ( n ) ise, o zaman bunu bu iki kuralla kanıtlamak, n ile tüm doğal sayılar için P ( n + b )' yi kanıtlamakla eşdeğerdir. bir indüksiyon temel durumu 0 .

Örnek: madeni paralarla dolar miktarları oluşturma

Sonsuz 4 ve 5 dolarlık madeni para arzı olduğunu varsayalım. Tümevarım, bu tür madeni paraların bir kombinasyonu ile 12'ye eşit veya daha büyük herhangi bir doların oluşturulabileceğini kanıtlamak için kullanılabilir . Let S ( k ) ifadesi "göstermek k dolar 4- ve 5 dolarlık paralar bir kombinasyonu ile oluşturulabilir ". Kanıtı S ( k ) her için de geçerlidir k 12 ≥ daha sonra endüksiyon ile elde edilebilir k , aşağıdaki gibi:

Temel durum : S ( k )' nin k = 12 için geçerli olduğunu göstermek basittir: üç adet 4 dolarlık madeni para alın.

İndüksiyon aşaması : göz önüne alındığında S ( k ) bir kısmı değeri için de geçerlidir k ≥ 12 ( indüksiyon hipotezi ), kanıtlamak S ( k + 1) , çok sahiptir:

Bazı keyfi k ≥ 12 için S ( k )' nin doğru olduğunu varsayın . En az bir 4 dolarlık madeni para içeren k dolar için bir çözüm varsa, k + 1 dolar yapmak için 5 dolarlık bir madeni para ile değiştirin . Aksi takdirde, sadece 5 dolarlık madeni paralar kullanılıyorsa, k , 5'in katı ve dolayısıyla en az 15 olmalıdır; ama sonra k + 1 dolar yapmak için üç adet 5 dolarlık madeni parayı dört adet 4 dolarlık madeni para ile değiştirebiliriz . Her durumda, S ( k + 1) doğrudur.

Bu nedenle, tümevarım ilkesine göre, S ( k ) tüm k ≥ 12 için geçerlidir ve ispat tamamlanmıştır.

Bu örnekte, S ( k ) için de geçerli olmasına rağmen , yukarıdaki ispat, minimum 12 dolarlık miktarı daha düşük bir değerle değiştirecek şekilde değiştirilemez m . İçin m = 11 , temel durum aslında yanlış olduğu; için m = 10 , indüksiyon aşamasında ikinci durumda iş değildir (dört 4 dolarlık paralar ile üç 5- yerine); hatta daha düşük m için bırakın . ${\textstyle k\in \{4,5,8,9,10\}}$

Birden fazla sayaçta indüksiyon

Bazen , tümevarım sürecini yineleyerek , n ve m olmak üzere iki doğal sayıyı içeren bir ifadeyi kanıtlamak istenir . Yani, n için bir temel durum ve bir endüktif adım kanıtlanır ve bunların her birinde m için bir temel durum ve bir endüktif adım kanıtlanır . Örneğin, doğal sayıların toplanmasına eşlik eden değişmeliliğin kanıtına bakın . Üç veya daha fazla sayacı içeren daha karmaşık argümanlar da mümkündür.

sonsuz iniş

Sonsuz iniş yöntemi, Pierre de Fermat tarafından kullanılan matematiksel tümevarımın bir varyasyonudur . Tüm n doğal sayıları için Q ( n ) ifadesinin yanlış olduğunu göstermek için kullanılır . Geleneksel biçimi, eğer Q ( n ) bazı doğal sayılar n için doğruysa , aynı zamanda kesinlikle daha küçük bir doğal sayı m için de geçerli olduğunu göstermekten ibarettir . Doğal sayıların sonsuz azalan dizisi olmadığı için, bu durum imkansız olurdu ve (çelişkiyle) Q ( n )'nin herhangi bir n için doğru olamayacağını gösterirdi .

Bu yöntemin geçerliliği, genel matematiksel tümevarım ilkesinden doğrulanabilir. " Q ( m ) m'den küçük veya n'ye eşit tüm doğal sayılar için yanlıştır " olarak tanımlanan P ( n ) ifadesinde matematiksel tümevarım kullanıldığında , P ( n )'nin tüm n için geçerli olduğu sonucu çıkar, yani Q ( n) ) her doğal sayı n için yanlıştır .

önek indüksiyon

Matematiksel tümevarımla ispatın en yaygın şekli, tümevarımsal adımda kanıtlamayı gerektirir.

${\displaystyle \forall k(P(k)\to P(k+1))}$

bunun üzerine tümevarım ilkesi , bu adımın n uygulamasını P (0) dan P ( n )' ye almada "otomatikleştirir" . Bu, "öncül tümevarım" olarak adlandırılabilir, çünkü her adım, o sayının öncülü hakkında bir şeyden bir sayı hakkında bir şey kanıtlar.

Hesaplama karmaşıklığına ilgi duyulan bir türev, endüktif adımda aşağıdaki ifadenin kanıtlandığı "ön ek tümevarım" dır:

${\displaystyle \forall k(P(k)\to P(2k)\land P(2k+1))}$

Veya eşdeğer olarak

${\displaystyle \forall k\left(P\sol(\left\lfloor {\frac {k}{2}}\sağ\rfloor \sağ)\to P(k)\sağa)}$

Tümevarım ilkesi daha sonra bu çıkarımın log n uygulamalarını P (0) 'dan P ( n )' ye almada "otomatikleştirir" . Aslında buna "ön ek indüksiyonu" denir, çünkü her adım, o sayının "ön eki" ile ilgili bir şeyden bir sayı hakkında bir şey kanıtlar - ikili gösteriminin düşük bitinin kesilmesiyle oluşturulduğu gibi. Aynı zamanda, bu ikili gösterimin uzunluğu üzerinde geleneksel tümevarımın bir uygulaması olarak da görülebilir.

Geleneksel öncül tümevarım hesaplamalı olarak n adımlı bir döngü olarak yorumlanırsa , önek tümevarım bir log- n adımlı döngüye karşılık gelir . Bu nedenle, önek tümevarım kullanan ispatlar, önceki tümevarım kullanan ispatlardan "daha uygulanabilir bir şekilde yapıcıdır".

Öncül tümevarım, aynı ifadede önek tümevarımını önemsiz bir şekilde simüle edebilir. Ön ek indüksiyonu, öncül tümevarımı simüle edebilir, ancak yalnızca ifadeyi sözdizimsel olarak daha karmaşık hale getirme pahasına (sınırlı bir evrensel niceleyici ekleyerek ), bu nedenle önek tümevarımını polinom-zaman hesaplamasına ilişkin ilginç sonuçlar, sınırsız niceleyicileri tamamen dışlamaya ve değişimi sınırlamaya bağlıdır. ifadede izin verilen sınırlı evrensel ve varoluşsal niceleyicilerin sayısı .

Fikir bir adım daha ileri götürülebilir:

${\displaystyle \forall k\left(P\sol(\left\lfloor {\sqrt {k}}\sağ\rzemin \sağ)\to P(k)\sağa)}$

bunun üzerine tümevarım ilkesi , bu çıkarımın log log n uygulamalarını P (0) 'dan P ( n )' ye almada "otomatikleştirir" . Bu tümevarım biçimi, benzer şekilde log-time paralel hesaplamayı incelemek için kullanılmıştır.

Tam (güçlü) indüksiyon

Olarak adlandırılan başka bir varyantı, tam indüksiyon , ders değerleri indüksiyon veya güçlü indüksiyonu (indüksiyon temel formu bazen olarak bilinen aksine zayıf indüksiyon ), daha güçlü bir hipotezi kullanarak kanıtlamak için endüktif adım kolaylaştırır: bir ifade kanıtlar altında ' den küçük tüm doğal sayılar için geçerli olan varsayım ; aksine, temel biçim yalnızca . "Güçlü tümevarım" adı, bu yöntemin "zayıf tümevarımdan" daha fazlasını kanıtlayabileceği anlamına gelmez, ancak yalnızca tümevarım adımında kullanılan daha güçlü hipoteze atıfta bulunur. ${\ Displaystyle P(m+1)}$${\görüntüleme stili P(n)}$${\görüntüleme stili n}$${\ Displaystyle m+1}$${\görüntüleme stili P(m)}$

Aslında, aşağıda açıklandığı gibi, iki yöntemin aslında eşdeğer olduğu gösterilebilir. Bu tam tümevarım biçiminde, yine de temel durumu kanıtlamak gerekir ve hatta aşağıdaki Fibonacci sayısı örneğinde olduğu gibi, genel argüman uygulanmadan önce olduğu gibi ekstra temel durumları kanıtlamak bile gerekli olabilir . ${\görüntüleme stili P(0)}$${\görüntüleme stili P(1)}$${\displaystyle F_{n}}$

Az önce açıklanan form, birinin temel durumu kanıtlamasını gerektirse de, herkes için kanıtlayabiliyorsa ( tümünün daha düşük olduğu varsayılarak ) bu gereksizdir . Bu , her ne kadar artık sıradan tümevarıma eşdeğer olmasa da, aşağıda açıklandığı gibi sonlu tümevarımın özel bir durumudur . Bu formda, temel durum, başka bir varsayımla kanıtlanmadığı durumda , davaya dahil edilir; bu vakanın ayrı olarak ele alınması gerekebilir, ancak bazen aynı argüman ve için de geçerlidir , bu da ispatı daha basit ve daha zarif hale getirir. Bununla birlikte, bu yöntemde, örneğin "keyfi seç" diyerek veya bir m öğe kümesinin bir öğeye sahip olduğunu varsayarak , kanıtının zımnen olarak varsaymadığından emin olmak hayati önem taşır . ${\görüntüleme stili P(m)}$${\görüntüleme stili P(n)}$${\görüntüleme stili n}$${\görüntüleme stili m\geq 0}$${\görüntüleme stili m=0}$${\görüntüleme stili P(0)}$${\görüntüleme stili P(n)}$${\görüntüleme stili m=0}$${\görüntüleme stili m>0}$${\görüntüleme stili P(m)}$${\görüntüleme stili m>0}$${\görüntüleme stili n<m}$

Tam tümevarım, bir yöntemin ispatının diğerinin bir ispata dönüştürülebilmesi anlamında, yukarıda açıklandığı gibi sıradan matematiksel tümevarıma eşdeğerdir. Diyelim ki tam tümevarım yoluyla bir kanıt var . Let ortalama " herkes için geçerlidir böyle ". Sonra herkes için geçerlidir ancak ve ancak herkes için geçerlidir ve bizim kanıtı kolayca bir kanıtı dönüştürülür (sıradan) indüksiyonla. Öte yandan, sıradan tümevarımla kanıtlansaydı, kanıt zaten tam tümevarımla bir tane olurdu: Temel durumda kanıtlanır, hiçbir varsayım kullanılmaz ve tümevarım adımında kanıtlanır, burada tüm varsayımlar yapılabilir. daha önceki durumlarda, ancak yalnızca davayı kullanmanız gerekir . ${\görüntüleme stili P(n)}$${\görüntüleme stili Q(n)}$${\görüntüleme stili P(m)}$${\görüntüleme stili m}$${\displaystyle 0\leq m\leq n}$${\görüntüleme stili Q(n)}$${\görüntüleme stili n}$${\görüntüleme stili P(n)}$${\görüntüleme stili n}$${\görüntüleme stili P(n)}$${\görüntüleme stili Q(n)}$${\görüntüleme stili P(n)}$${\görüntüleme stili P(0)}$${\görüntüleme stili P(n+1)}$${\görüntüleme stili P(n)}$

Örnek: Fibonacci sayıları

Tam tümevarım, her bir tümevarımsal adım için tümevarımsal hipotezin birkaç örneğinin gerekli olduğu durumlarda en kullanışlıdır. Örneğin, tam tümevarım bunu göstermek için kullanılabilir.

${\displaystyle F_{n}={\frac {\varphi ^{n}-\psi ^{n}}{\varphi -\psi }}}$

burada bir N inci Fibonacci sayısı , ( altın oran ) ve polinom kökleridir . Her biri için , yukarıdaki özdeşliğin , hem ve hem de için zaten geçerli olduğu varsayılırsa, doğrudan hesaplama ile doğrulanabileceği gerçeğini kullanarak . Kanıtı tamamlamak için kimliğin iki temel durumda doğrulanması gerekir: ve . ${\displaystyle F_{n}}$${\textstyle \varphi ={{1+{\sqrt {5}}} \2'den fazla}}$${\textstyle \psi ={{1-{\sqrt {5}}} \2'den fazla}}$${\displaystyle x^{2}-x-1}$${\displaystyle F_{n+2}=F_{n+1}+F_{n}}$${\displaystyle n\in {\mathbb {N}}}$${\textstyle F_{n+2}}$${\textstyle F_{n+1}}$${\textstyle F_{n}}$${\görüntüleme stili n=0}$${\metin stili n=1}$

Örnek: asal çarpanlara ayırma

Tam indüksiyonla başka kanıtı açıklamada için de geçerlidir hipotezini kullanan tüm küçük daha iyice. Aritmetiğin temel teoreminin " varlık " kısmı olan " 1'den büyük her doğal sayı (bir veya daha fazla) asal sayının çarpımıdır " ifadesini ele alalım . Endüktif adımı kanıtlamak için, tümevarım hipotezi, verilen bir ifade için tüm küçükler için geçerli olmasıdır . Asal ise , o zaman kesinlikle asal sayıların bir çarpımıdır ve değilse, tanım gereği bir çarpımdır: , burada hiçbir faktör 1'e eşit değildir; dolayısıyla hiçbiri 'ye eşit değildir ve bu nedenle her ikisi de 1'den büyük ve 'den küçüktür . Tümevarım hipotezi şimdi ve için geçerlidir , dolayısıyla her biri asal sayıların bir ürünüdür. Böylece , asal sayıların çarpımıdır ve dolayısıyla, asal sayıların kendisinin bir çarpımıdır. ${\görüntüleme stili n}$${\görüntüleme stili n>1}$${\görüntüleme stili n>1}$${\görüntüleme stili m}$${\displaystyle m=n_{1}n_{2}}$${\görüntüleme stili m}$${\görüntüleme stili m}$${\görüntüleme stili n_{1}}$${\ Displaystyle n_{2}}$${\görüntüleme stili m}$

Örnek: yeniden ziyaret edilen dolar tutarları

Yukarıdakiyle aynı örneği bu sefer güçlü tümevarımla kanıtlamaya çalışacağız . Açıklama aynı kalır:

${\displaystyle S(n):\,\n\geq 12\to \,\vardır \,a,b\in \mathbb {N} .\,\,n=4a+5b}$

Ancak, genişletilmiş temel durumdan başlayarak, ispatın yapısında ve varsayımlarında küçük farklılıklar olacaktır:

Temel durum : Bunun için geçerli olduğunu gösterin . ${\görüntüleme stili S(k)}$${\görüntüleme stili k=12,13,14,15}$

${\displaystyle {\begin{hizalanmış}4\cdot 3+5\cdot 0=12\\4\cdot 2+5\cdot 1=13\\4\cdot 1+5\cdot 2=14\\4\ cdot 0+5\cdot 3=15\end{hizalı}}}$

Temel durum tutar.

İndüksiyon hipotezi : Bazı Verilen farz herkes için geçerlidir ile . ${\ Displaystyle j>15}$${\görüntüleme stili S(m)}$${\görüntüleme stili m}$${\displaystyle 12\leq m<j}$

Endüktif adım : Bunun geçerli olduğunu kanıtlayın . ${\görüntüleme stili S(j)}$

Tümevarım hipotezi ile seçilmesi ve gözlemlenmesi bunun geçerli olduğunu gösterir . Yani, toplam ve dolar madeni paralarının bir kombinasyonu ile oluşturulabilir . Ardından, bu kombinasyona bir dolar madeni para eklemek , toplamı verir . Yani tutar. QED ${\görüntüleme stili m=j-4}$${\displaystyle 15<j\to 12\leq j-4<j}$${\görüntüleme stili S(j-4)}$${\görüntüleme stili j-4}$${\görüntüleme stili 4}$${\görüntüleme stili 5}$${\görüntüleme stili 4}$${\görüntüleme stili j}$${\görüntüleme stili S(j)}$

İleri-geri indüksiyon

Bazen, için geçerliliği göz önüne alındığında , ifadesini kanıtlayarak geriye doğru sonuç çıkarmak daha uygundur . Ancak, tek bir sayı için ifadenin geçerliliğini kanıtlamak, temel durumu oluşturmak için yeterli değildir; bunun yerine, doğal sayıların sonsuz bir alt kümesi için ifadeyi kanıtlamak gerekir. Örneğin, Augustin Louis Cauchy önce 2'nin tüm kuvvetleri için aritmetik ve geometrik araçların eşitsizliğini kanıtlamak için ileri (düzenli) tümevarım kullandı ve ardından tüm doğal sayılar için bunu göstermek için geriye doğru tümevarım kullandı. ${\görüntüleme stili n-1}$${\görüntüleme stili n}$

Endüktif adımda hata örneği

Tüm n değerleri için endüktif adım kanıtlanmalıdır . Bunu açıklamak için Joel E. Cohen, tüm atların aynı renkte olduğunu matematiksel tümevarımla kanıtlamayı iddia eden aşağıdaki argümanı önerdi :

• Temel durum: Yalnızca bir attan oluşan bir sette yalnızca bir renk vardır.
• Tümevarım adımı: Herhangi bir at kümesinde yalnızca bir renk olduğunu tümevarım hipotezi olarak varsayın . Şimdi herhangi bir at setine bakın . Numaralandırın: . kümeleri düşünün ve . Her biri yalnızca atlardan oluşan bir settir , bu nedenle her birinin içinde yalnızca bir renk vardır. Ancak iki takım örtüşüyor, bu yüzden tüm atlar arasında sadece bir renk olmalı .${\görüntüleme stili n}$${\ Displaystyle n+1}$${\displaystyle 1,\;2,\;3,\;\dotsc ,\;n,\;n+1}$${\textstyle \sol\{1,\;2,\;3,\;\dotsc ,\;n\sağ\}}$${\textstyle \sol\{2,\;3,\;4,\;\dotsc ,\;n+1\sağ\}}$${\görüntüleme stili n}$${\ Displaystyle n+1}$

Temel durum önemsizdir (her at kendisiyle aynı renkte olduğundan) ve tümevarım adımı her durumda doğrudur . Bununla birlikte, tümevarımsal adımın mantığı, "iki küme örtüşüyor" ifadesi yanlış olduğu için yanlıştır (yalnızca çıkarmadan önce atlar vardır ve çıkarmadan sonra, bir atın kümelerinin her biri örtüşmez). ${\görüntüleme stili n=1}$${\görüntüleme stili n>1}$${\görüntüleme stili n=1}$${\görüntüleme stili n+1=2}$

Resmileştirme

İn ikinci dereceden mantığı , bir "yazabiliriz aksiyomuna şöyle indüksiyon":

${\displaystyle \forall P{\Bigl (}P(0)\land \forall k{\bigl (}P(k)\to P(k+1){\bigr )}\to \forall n{\bigl (}P(n){\büyük )}{\Büyük )}}$,

burada P (.), bir doğal sayı içeren yüklemler için bir değişkendir ve k ve n , doğal sayılar için değişkenlerdir .

Bir deyişle, temel durum P (0) ve indüktif aşama (yani, indüksiyon hipotezi P ( k ) ifade eder p ( k + 1) birlikte olduğu anlamına) P ( n ) herhangi bir doğal sayı n . Tümevarım aksiyomu , temel durumdan ve tümevarım adımından P ( n )' nin herhangi bir doğal sayı n için geçerli olduğu sonucunu çıkarmanın geçerliliğini ileri sürer .

Aksiyomdaki ilk niceleyici, bireysel sayılar yerine yüklemlere göre değişir . Bu, ikinci dereceden bir niceleyicidir, bu, bu aksiyomun ikinci dereceden mantıkta ifade edildiği anlamına gelir . Birinci dereceden mantıkta aksiyomlayıcı aritmetik tümevarım, her olası yüklem için ayrı bir aksiyom içeren bir aksiyom şeması gerektirir . Peano aksiyomları makalesi bu konuyla ilgili daha fazla tartışma içeriyor.

Doğal sayılar için yapısal tümevarım aksiyomu ilk olarak, aşağıdaki diğer dört aksiyomla birlikte doğal sayıları belirtmek için kullanan Peano tarafından formüle edildi:

1. 0 bir doğal sayıdır.
2. Her doğal sayının ardıl işlevi s bir doğal sayı verir ( s ( x ) = x + 1) .
3. Ardıl işlevi injektiftir.
4. 0 olmadığı aralık ait s .

Gelen ilk sipariş ZFC küme teorisi , yüklemler üzerinde ölçümü izin verilmez, ancak hala setleri üzerinde ölçümü ile indüksiyon ifade edebilirsiniz:

${\displaystyle \forall A{\Bigl (}0\in A\land \forall k\in \mathbb {N} {\bigl (}k\in A\to (k+1)\in A{\bigr ) }\to \mathbb {N} \subseteq A{\Bigr )}}$

A , bir önermeyi temsil eden ve önermenin geçerli olduğu doğal sayıları içeren bir küme olarak okunabilir. Bu bir aksiyom değil, doğal sayıların ZFC küme teorisi dilinde, Peano'nunkine benzer aksiyomlarla tanımlandığı göz önüne alındığında bir teoremdir.

Sınır ötesi indüksiyon

Tam indüksiyon ilkesinin bir varyasyonu herhangi birinin elemanları ile ilgili ifadeler için de genelleştirilebilir iyi kurulmuş grubu , bir ile bir dizi, irreflexive ilişki bir içermektedir < sonsuz inen zincirleri . Bir sıra sayısını temsil eden her küme sağlam temellidir , doğal sayılar kümesi bunlardan biridir.

Sağlam temelli bir kümeye uygulanan transfinit tümevarım tek bir adım olarak formüle edilebilir. Her sıra numarası için bir P ( n ) ifadesinin geçerli olduğunu kanıtlamak için:

1. Her n sıra sayısı için , eğer P ( m ) tüm m < n için geçerliyse , o zaman P ( n )'nin de geçerli olduğunu gösterin .

Bu tümevarım biçimi, bir dizi sıra sayısına ( iyi sıralanmış ve dolayısıyla sağlam temelli bir sınıf oluşturan) uygulandığında , sonlu ötesi tümevarım olarak adlandırılır . Küme teorisi , topoloji ve diğer alanlarda önemli bir ispat tekniğidir .

Sınır ötesi tümevarımla yapılan ispatlar tipik olarak üç durumu ayırt eder:

1. zaman n, en az bir elemanın, diğer bir deyişle daha elemanının küçük olduğu , n ;
2. zaman n, yani daha küçük olan öğeleri kümesinin doğrudan selefi olan n bir en büyük elemanına sahiptir;
3. zaman n, doğrudan bir selefi olan, yani, n, bir sözde sınır sıra .

Kesin konuşmak gerekirse, bunun bir nedeni, bir baz davayı kanıtlamak için ötesi tümevarım gerekli değildir anlamsız eğer önermenin özel bir durum P tüm doğrudur n < m , daha sonra P doğrudur m . Kesinlikle doğrudur, çünkü karşı örnek olarak kullanılabilecek hiçbir n < m değeri yoktur . Yani özel durumlar, genel durumun özel durumlarıdır.

İyi sıralama ilkesiyle ilişkisi

Matematiksel tümevarım ilkesi genellikle doğal sayıların bir aksiyomu olarak ifade edilir ; Peano aksiyomlarına bakın . Diğer Peano aksiyomları bağlamında iyi sıralama ilkesinden kesinlikle daha güçlüdür . Aşağıdakileri varsayalım:

• Kısma bölünen aksiyomu: herhangi bir doğal sayı için , n ve m , n, e eşit veya bundan daha az olduğu m , ancak ve ancak, eğer m az değildir n .
• Her hangi bir sayı için , n , n + 1 büyüktür fazla n .
• Herhangi bir n doğal sayısı için , n ile n +1 arasında hiçbir doğal sayı yoktur .
• Hiçbir doğal sayı sıfırdan küçük değildir.

Daha sonra, yukarıda sıralanan aksiyomlar göz önüne alındığında, tümevarımın iyi sıralama ilkesini ima ettiği kanıtlanabilir. Aşağıdaki ispat, tam tümevarım ve birinci ve dördüncü aksiyomları kullanır.

Kanıt. En az elemanı olmayan doğal sayılardan oluşan boş olmayan bir S kümesi olduğunu varsayalım . Let P ( n ) olup ispat edilmesi , n değil S . O zaman P (0) doğrudur, çünkü eğer yanlışsa 0, S öğesinin en küçük öğesidir . Ayrıca, n bir doğal sayı olsun ve n + 1'den küçük tüm m doğal sayıları için P ( m )'nin doğru olduğunu varsayalım . Daha sonra, eğer P ( n + 1) yanlış , n + 1 olduğu S , böylece de en az bir öğesi olarak, S , bir çelişki. Böylece P ( n + 1) doğrudur. Bu nedenle, tam tümevarım ilkesine göre, P ( n ) tüm n doğal sayıları için geçerlidir ; yani S boş, bir çelişki. QED

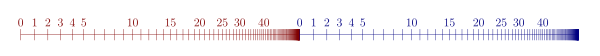
Öte yandan, resimde gösterilen {(0, n ): n ∈ ℕ} ∪ {(1, n ): n ∈ ℕ} kümesi sözlük sırasına göre iyi sıralanmıştır . Ayrıca, tümevarım aksiyomu dışında, Peano sabiti 0'ın çift (0,0) olarak yorumlandığı ve Peano'nun ardıl fonksiyonunun succ ( x , n ) = ( x , n + ile çiftler üzerinde tanımlandığı ) tüm Peano aksiyomlarını karşılar. 1) tüm x ∈{0,1} ve n ∈ℕ için. Tümevarım aksiyomunun ihlaline bir örnek olarak , bazı y için P ( x , n ) yüklemini ( x , n ) = (0, 0) veya ( x , n ) = ( succ ( y , m )) olarak tanımlayın ∈{0,1} ve m ∈ℕ. O zaman temel durum P (0,0) önemsiz derecede doğrudur ve adım durumu da öyle: eğer P ( x , n ) , o zaman P ( succ ( x , n ) ) . Ancak P , kümedeki tüm çiftler için doğru değildir.

Peano'nun tümevarım ilkesine sahip aksiyomları, doğal sayıları benzersiz bir şekilde modeller. Tümevarım ilkesini iyi sıralama ilkesiyle değiştirmek, tüm aksiyomları yerine getiren daha egzotik modellere izin verir.

İyi sıralama ilkesinin tümevarım aksiyomuna eşdeğer olduğu birçok kitap ve kaynakta yanlışlıkla basılmıştır. Diğer Peano aksiyomları bağlamında durum böyle değildir, ancak diğer aksiyomlar bağlamında bunlar eşdeğerdir; özellikle, iyi sıralama ilkesi, yukarıda listelenen ilk iki aksiyom bağlamında tümevarım aksiyomunu ima eder ve

• Her doğal sayı 0 ya da bir n + 1 bazı doğal için sayı n .

Birçok hatalı ispattaki yaygın hata, n - 1'in benzersiz ve iyi tanımlanmış bir doğal sayı olduğunu varsaymaktır; bu, diğer Peano aksiyomlarında ima edilmeyen bir özelliktir.

Ayrıca bakınız

• kombinatoryal kanıt
• İndüksiyon bulmacaları
• Yorgunluk kanıtı
• özyineleme
• Özyineleme (bilgisayar bilimi)
• yapısal indüksiyon
• Sınır ötesi indüksiyon

Notlar

Referanslar