Möbius dönüşümü - Möbius transformation
Olarak geometri ve kompleks analiz , bir Möbiüs dönüşüm ait kompleks düzlemde a, rasyonel fonksiyonu formunun
Geometrik olarak, bir Möbius dönüşümü, önce düzlemden iki küre birimine stereografik izdüşüm gerçekleştirerek , küreyi uzayda yeni bir konuma ve oryantasyona döndürerek ve hareket ettirerek ve daha sonra (kürenin yeni konumundan) stereografik izdüşüm gerçekleştirerek elde edilebilir. ) uçağa. Bu dönüşümler açıları korur, her düz çizgiyi bir çizgi veya daireyle eşler ve her daireyi bir çizgi veya daireyle eşler.
Möbius dönüşümleri , karmaşık yansıtmalı çizginin yansıtmalı dönüşümleridir . Projektif lineer grup PGL(2, C ) olan Möbius grubu adı verilen bir grup oluştururlar . Alt gruplarıyla birlikte matematik ve fizikte çok sayıda uygulamaya sahiptir.
Möbius dönüşümleri, Ağustos Ferdinand Möbius'un onuruna adlandırılmıştır ; bunlar aynı zamanda homografiler , homografik dönüşümler , doğrusal kesirli dönüşümler , çift doğrusal dönüşümler , kesirli doğrusal dönüşümler veya spin dönüşümleri (görecelik teorisi) olarak da adlandırılır .
genel bakış
Möbius dönüşümleri, genişletilmiş karmaşık düzlemde tanımlanır (yani, sonsuzdaki nokta tarafından büyütülmüş karmaşık düzlem ).
Stereografik izdüşüm , daha sonra Riemann küresi olarak adlandırılan bir küre ile özdeşleşir ; alternatif olarak, karmaşık projektif çizgi olarak düşünülebilir . Möbiüs dönüşümler tam olarak örten konformal kendi Riemann küreden haritaları, yani otomorfizmalar bir şekilde Riemann kürenin karmaşık bir çoklu ; alternatif olarak, bir cebirsel çeşitlilik olarak otomorfizmalardır . Bu nedenle, tüm Möbius dönüşümlerinin kümesi, bileşim altında bir grup oluşturur . Bu grup Möbius grubu olarak adlandırılır ve bazen olarak gösterilir .
Möbiüs grubu olduğu izomorfik yönlendirme koruyucu grubuna izometrileri arasında hiperbolik 3-alan ve çalışma, bu nedenle önemli bir rol oynar hiperbolik 3-manifoldlar .
Olarak fizik , kimlik bileşeni arasında Lorentz grubu üzerinde etkili gökküresi Möbiüs grubu Riemann küre üzerinde hareket aynı şekilde. Aslında, bu iki grup izomorfiktir. Göreceli hızlara hızlanan bir gözlemci, Dünya'nın yakınında görüldüğü gibi takımyıldız deseninin sonsuz küçük Möbius dönüşümlerine göre sürekli dönüştüğünü görecektir. Bu gözlem genellikle twistor teorisinin başlangıç noktası olarak alınır .
Möbius grubunun belirli alt grupları, diğer basit bağlantılı Riemann yüzeylerinin ( karmaşık düzlem ve hiperbolik düzlem ) otomorfizm gruplarını oluşturur . Bu nedenle, Möbius dönüşümleri Riemann yüzeyleri teorisinde önemli bir rol oynamaktadır . Temel grup , her Riemann yüzeyi a, ayrı alt-grup (bakınız Möbiüs grubunun Fuchsian grubu ve Kleinian grubu ). Möbius grubunun özellikle önemli bir ayrık alt grubu, modüler gruptur ; birçok teorisine merkezi fraktallar , modüler formlar , eliptik eğriler ve Pellian denklemler .
Möbiüs dönüşümler daha genel boyutun mekanlarda tanımlanabilir n den örten konformal yönlendirme koruyucu haritalar gibi> 2 N -sphere için n -sphere. Böyle bir dönüşüm, bir etki alanının uyumlu eşlemesinin en genel biçimidir. Göre Liouville teoremi bir Möbiüs dönüşüm çevirileri, bir bileşim olarak ifade edilebilir benzerlikler , ortogonal dönüşüm ve ters çevirme.
Tanım
Bir Möbius dönüşümünün genel biçimi şu şekilde verilir:
c ≠ 0 durumunda , bu tanım tanımlanarak tüm Riemann küresine genişletilir.
Eğer c = 0 , tanımladığımızı
Bu nedenle, bir Möbius dönüşümü her zaman Riemann küresinden Riemann küresine bir bijektif holomorfik fonksiyondur .
Tüm Möbius dönüşümlerinin kümesi, bileşim altında bir grup oluşturur . Bu gruba karmaşık bir manifoldun yapısı, kompozisyon ve inversiyon holomorfik haritalar olacak şekilde verilebilir . Möbius grubu daha sonra karmaşık bir Lie grubudur . Möbius grubu, genellikle Riemann küresinin otomorfizm grubu olduğu için belirtilir .
Sabit noktalar
Her özdeş olmayan Möbius dönüşümünün Riemann küresi üzerinde iki sabit noktası vardır . Sabit noktalar burada sayılır bu Not çokluğu ; parabolik dönüşümler, sabit noktaların çakıştığı dönüşümlerdir. Bu sabit noktalardan biri veya her ikisi sonsuzdaki nokta olabilir.
Sabit noktaların belirlenmesi
Dönüşümün sabit noktaları
Tüm C = 0, lineer bir denklem haline kuadratik denklemi dejenere ve dönüşümü doğrusaldır. Bu, sabit noktalardan birinin sonsuzdaki nokta olduğu duruma karşılık gelir. Ne zaman bir ≠ d ikinci sabit nokta sonlu ve verilir
Bu durumda dönüşüm, ötelemeler , döndürmeler ve genişlemelerden oluşan basit bir dönüşüm olacaktır :
Eğer c = 0 ve bir = d , o zaman her iki sabit noktalar saf çeviri Möbiüs dönüşümü karşılık sonsuzda, ve:
topolojik kanıt
Topolojik olarak, (özdeşlik-olmayan) Möbius dönüşümlerinin 2 noktayı (çoklukla) sabitlemesi , kürenin Euler karakteristiğine karşılık gelir :
İlk olarak, projektif lineer grup PGL(2, K ) keskin bir şekilde 3-geçişlidir - farklı noktaların herhangi iki sıralı üçlüsü için, tıpkı Möbius dönüşümlerinde olduğu gibi ve aynı şekilde bir üçlüyü diğerine alan benzersiz bir harita vardır. cebirsel kanıt ( grup 3 boyutlu olduğu için esasen boyut sayımı ). Böylece en az 3 noktayı sabitleyen herhangi bir harita kimliktir.
Daha sonra, Möbius grubunu herhangi bir Möbius fonksiyonunun özdeşliğe homotopik olduğu ile tanımlayarak görebiliriz . Aslında, genel lineer grubun herhangi bir üyesi Gauss-Jordan eliminasyonu ile kimlik haritasına indirgenebilir, bu, projektif lineer grubun da yola bağlı olduğunu ve kimlik haritasına bir homotopi sağladığını gösterir. Lefschetz-Hopf teoremi sonlu sayıda sabit noktaları ile bir haritanın sabit nokta (bu bağlamda, çokluk) indislerinin toplamı eşittir bildiren Lefschetz sayısı bu durumda kimlik haritasının izidir haritanın, Euler karakteristiği olan homoloji grupları üzerinde.
Buna karşılık, gerçek yansıtmalı çizginin, PGL(2, R ) projektif lineer grubunun herhangi bir noktayı sabitlemesine gerek yoktur – örneğin (gerçek) sabit noktaları yoktur: karmaşık bir dönüşüm olarak sabitler ± i – harita 2 x sabitlerken 0 ve ∞'nin iki noktası. Bu, dairenin (gerçek yansıtmalı doğru) Euler karakteristiğinin 0 olduğu gerçeğine tekabül eder ve bu nedenle Lefschetz sabit nokta teoremi yalnızca en az 0 noktayı, ancak muhtemelen daha fazlasını sabitlemesi gerektiğini söyler.
Normal form
Möbius dönüşümleri de bazen normal formda sabit noktaları cinsinden yazılır . Önce iki ayrı sabit noktanın olduğu parabolik olmayan durumu ele alıyoruz.
Parabolik olmayan durum :
Parabolik olmayan her dönüşüm, bir genişleme/dönüşe, yani formun bir dönüşümüne eşleniktir .
Eğer f ayrı sabit noktaları vardır ( γ 1 , y 2 ) daha sonra dönüştürme 0 ° C'de sabit noktaya sahiptir ve ∞ ve bu nedenle büyümesidir: . Daha sonra f dönüşümü için sabit nokta denklemi yazılabilir.
f'yi çözmek (matris formunda):
Yukarıdaki ifadelerden , sabit noktalarda f'nin türevleri hesaplanabilir :
Gözlemleyin, sabit nokta bir sipariş göz önüne alındığında, çarpanların (birini ayırt edebilir k arasında) f olarak karakteristik sabit bir f . Sabit noktaların sırasını tersine çevirmek, karakteristik sabit için ters çarpanı almaya eşdeğerdir:
Loxodromic dönüşümler için, her zaman | k | > 1, kimse bu γ diyor 1 olan itici sabit nokta ve γ 2 olan cazip sabit nokta. için | k | < 1, roller tersine çevrilir.
Parabolik durum :
Parabolik durumda sadece bir sabit nokta γ vardır . Bu noktayı ∞'ye gönderen dönüşüm
Burada β, öteleme uzunluğu olarak adlandırılır . Bir parabolik dönüşüm için sabit nokta formülü daha sonra
f (matris formunda) için çözme verir
Not β olan olup karakteristik sabit f her zaman parabolik dönüşüm için 1,. Yukarıdaki ifadelerden hesaplanabilir:
Dönüşümün kutupları
Noktası olarak adlandırılır kutup arasında ; altında sonsuzdaki noktaya dönüştürülen noktadır .
Ters kutup , sonsuzdaki noktanın dönüştürüldüğü noktadır. İki kutup arasındaki orta nokta her zaman iki sabit nokta arasındaki orta nokta ile aynıdır:
Bu dört nokta , bazen dönüşümün karakteristik paralelkenarı olarak adlandırılan bir paralelkenarın köşeleridir .
Bir dönüşüm , iki sabit nokta γ 1 , γ 2 ve kutup ile belirtilebilir .
Bu, k ile verilen arasındaki dönüşüm için bir formül türetmemizi sağlar :
Son ifade , matrisin (karşılıklı olarak karşılıklı) özdeğer oranlarından biriyle çakışıyor
Basit Möbius dönüşümleri ve kompozisyon
Bir Möbius dönüşümü, basit dönüşümler dizisi olarak oluşturulabilir .
Aşağıdaki basit dönüşümler de Möbius dönüşümleridir:
- bir çeviridir .
- a ( homotety ve rotasyon ) birleşimidir . Eğer bu bir rotasyon olduğunu, sonra eğer o zaman bir ispatlarda olduğunu.
- ( gerçek eksene göre ters çevirme ve yansıma )
Basit dönüşümlerin bileşimi
Eğer , izin verin:
- ( Çevirisi tarafından d / c )
- ( gerçek eksene göre ters çevirme ve yansıma )
- ( homotety ve rotasyon )
- ( a / c ile çeviri )
Daha sonra bu fonksiyonlar oluşturulabilir ,
Yani,
Bu ayrıştırma, Möbius dönüşümünün birçok özelliğini açık hale getirir.
Temel özellikler
Bir Möbius dönüşümü, bir dizi daha basit dönüşüme eşdeğerdir. Kompozisyon, Möbius dönüşümünün birçok özelliğini açık hale getirir.
Ters dönüşüm için formül
Ters Möbius dönüşümünün varlığı ve açık formülü, daha basit dönüşümlerin ters fonksiyonlarının bileşimi ile kolayca elde edilir. İşlevler tanımlayan bir O g 1 , g 2 , g 3 , g 4 gibi her birinin g i tersidir f i . Daha sonra kompozisyon
Açıların ve genelleştirilmiş çemberlerin korunması
Bu ayrıştırmadan, Möbius dönüşümlerinin daire tersinin önemsiz olmayan tüm özelliklerini taşıdığını görüyoruz . Örneğin, açıların korunması, diğer dönüşüm türleri, açıları önemsiz bir şekilde koruyan genişleme ve izometriler (çevirme, yansıma, döndürme) olduğundan, daire ters çevrilmesinin açıları koruduğunu kanıtlamaya indirgenir .
Ayrıca, Möbiüs dönüşümler edilen haritanın çevreleri genel daire ters bu özelliğine sahip olduğundan genel çevrelere. Genelleştirilmiş bir daire ya bir daire ya da bir çizgidir, ikincisi sonsuzdaki noktadan geçen bir daire olarak kabul edilir. Bir Möbius dönüşümünün mutlaka daireleri dairelere ve çizgileri çizgilere eşlemediğini unutmayın: ikisini karıştırabilir. Bir daireyi başka bir daireyle eşlese bile, ilk dairenin merkezini ikinci dairenin merkezine eşlemesi gerekmez.
Çapraz oranlı koruma
Çapraz oranlar , Möbius dönüşümleri altında değişmezdir. Diğer bir deyişle, bir Möbius dönüşümü dört farklı noktayı sırasıyla dört farklı noktaya eşlerse, o zaman
Noktalardan biri sonsuzdaki nokta ise, çapraz oran uygun limit alınarak tanımlanmalıdır; örneğin çapraz oranı IS
Dört farklı noktanın çapraz oranı, ancak ve ancak içlerinden geçen bir çizgi veya daire varsa gerçektir. Bu, Möbius dönüşümlerinin genelleştirilmiş daireleri koruduğunu göstermenin başka bir yoludur.
Birleşme
İki puan z 1 ve Z 2 olan konjügatı genelleştirilmiş bir daireye göre Cı eğer, genel bir daire verilen D içinden geçen z 1 ve z 2 ve kesme C iki noktadan bir ve b , ( z 1 , z 2 ; a , b ) olan harmonik çapraz oranı (yani, çapraz oranı 1). Bu özellik, D çemberinin seçimine bağlı değildir . Bu özellik bazen bir çizgiye veya daireye göre simetrik olarak da adlandırılır .
İki z , z ∗ noktası , eğer doğruya göre simetrikse , bir doğruya göre eşleniktir . Bu daireye göre ters çevirme ile yer değiştirirlerse, iki nokta bir daireye göre eşleniktir .
Nokta z * konjuge z L tabanlı vektör ile tespit hattı E iθ noktasında z 0 açık olarak verilebilir
Nokta z * konjuge z Cı yarıçapı çemberi r merkezli z 0 açık olarak verilebilir
Möbius dönüşümleri genelleştirilmiş çemberleri ve çapraz oranları koruduğu için, aynı zamanda konjugasyonu da korurlar.
Projektif matris temsilleri
Doğal aksiyon PGL (2, Cı üzerine) kompleksi yansıtmalı hattı CP 1 tam yansıtmalı hattı Riemann küre, Möbius grubunun doğal eylem CP 1 aşağıdaki gibi ve Riemann küre tanımlanır:
Her tersinir kompleks 2×2 matrisi ile
İki matrisin çarpımının , karşılık gelen iki Möbius dönüşümünün bileşimi ile ilişkilendirileceğini kontrol etmek kolaydır . Başka bir deyişle, harita
Karmaşık bir skaler λ ile çarpılarak elde edilen herhangi bir matrisin aynı dönüşümü belirlediğine dikkat edin, bu nedenle bir Möbius dönüşümü matrisini yalnızca skaler katlara
kadar belirler . Başka bir deyişle: π'nin çekirdeği , I kimlik matrisinin tüm skaler katlarından oluşur ve grup teorisinin ilk izomorfizm teoremi , GL(2, C ) / (( C \ {0}) I ) bölüm grubunun Möbius grubuna göre izomorfiktir. Bu bölüm grubu projektif lineer grup olarak bilinir ve genellikle PGL(2, C ) ile gösterilir.Eğer biri determinantın matrisleriyle sınırlandırılırsa ,
π haritası özel lineer grup SL(2, C )'den Möbius grubuna bir surjective harita ile sınırlandırılır ; kısıtlı ortamda çekirdek artı ve eksi özdeşlikten oluşur ve PSL(2, C ) ile gösterilen SL(2, C ) / {± I } bölüm grubu da bu nedenle Möbius grubuna eşbiçimlidir:Herhangi bir Möbius dönüşümünü temsil etmek için kullanılabilecek, birim determinantı olan tam olarak iki matris olduğuna dikkat edin. Yani, SL(2, C ), PSL(2,
C )' nin çift kapağıdır . SL(2, C ) basit bağlantılı olduğundan , Möbius grubunun evrensel kapağıdır . Bu nedenle, Möbius grubunun temel grubu Z 2'dir .Üç nokta ile bir dönüşüm belirtme
Riemann küresi üzerinde üç farklı nokta z 1 , z 2 , z 3 ve w 1 , w 2 , w 3 farklı noktalardan oluşan ikinci bir set verildiğinde ,
f ( z i ) ile tam olarak bir Möbius dönüşümü f ( z ) vardır. ) = w i için i 1,2,3 =. (Başka bir deyişle: Möbius grubunun Riemann küresi üzerindeki eylemi keskin bir şekilde 3-geçişlidir .) Verilen nokta kümelerinden f ( z )' yi belirlemenin birkaç yolu vardır .Önce 0, 1, ∞ ile eşleme
Möbius dönüşümünü kontrol etmek kolaydır.
Eğer Benzer eşlemek için tanımlandığı
ağırlık , 1 , ağırlık 2 , ağırlık 3 , 0 1, ∞, daha sonra matris haritalar z 1,2,3 için ağırlık 1,2,3 olur{0, 1, ∞} stabilizatörü (sırasız bir küme olarak) anharmonik grup olarak bilinen bir alt
gruptur .Açık belirleyici formül
denklem
Möbius grubunun alt grupları
Bir Möbius dönüşümünün a , b , c , d katsayılarının ad − bc = 1 olan gerçek sayılar olmasını istersek, Möbius grubunun PSL(2, R ) olarak gösterilen bir alt grubunu elde ederiz . Bu harita, bu Möbiüs dönüşümlerinin grubudur üst yarı düzlem H = x + i y : y > 0 kendisine ve tüm grubundan eşit biholomorphic (ya da eşit şekilde: örten , konformal ve yönlendirme koruyucu) haritalar H → H . Uygun ise mt sokulur, üst yarı düzlem bir model haline hiperbolik düzlemde H 2 , Poincare yarı düzlem modeli ve PSL (2, R ) her yönlendirme koruyucu izometrileri grubudur H 2 bu modeli.
Açık diski eşleyen tüm Möbius dönüşümlerinin alt grubu D = z : | z | < 1 kendisine formun tüm dönüşümlerinden oluşur
Yukarıdaki alt her ikisinin izometri gruplar olarak görev yana H 2 , bu izomorfik. Dönüşüm ile konjugasyon yoluyla somut bir izomorfizm verilir
Alternatif olarak, r yarıçaplı ve r i merkezli bir açık disk düşünün . Bu diskteki Poincare disk modeli, r ∞'ye yaklaştıkça üst yarı düzlem modeliyle aynı hale gelir .
Möbius grubunun bir maksimal kompakt alt grubu (
Tóth 2002 ) ile verilir.Katsayıları gerektiriyorsa bir , b , c , d bir Möbiüs dönüşüm için tam sayıları ile reklam - bc = 1, elde ederiz modüler grubu PSL (2, Z ), PSL ayrı bir alt grubunu (2, R ) önemli olarak karmaşık düzlemde kafeslerin incelenmesi , eliptik fonksiyonlar ve eliptik eğriler . PSL(2, R )' nin ayrık alt grupları , Fuşya grupları olarak bilinir ; Riemann yüzeylerinin çalışmasında önemlidirler .
sınıflandırma

Aşağıdaki tartışmada her zaman temsil eden matrisin şu şekilde normalize edildiğini varsayacağız .
Özdeş olmayan Möbius dönüşümleri genel olarak parabolik , eliptik , hiperbolik ve loksodromik olmak üzere dört tipte sınıflandırılır ve hiperbolik olanlar loksodromik olanların bir alt sınıfıdır. Sınıflandırmanın hem cebirsel hem de geometrik önemi vardır. Geometrik olarak, farklı türler, aşağıdaki şekillerde gösterildiği gibi, karmaşık düzlemin farklı dönüşümleriyle sonuçlanır.
Bu dört tip, ize bakılarak ayırt edilebilir . İznin konjugasyon altında değişmez olduğuna dikkat edin , yani,
parabolik dönüşümler
Bir matris ile tanımlanan bir kimlik Möbiüs dönüşümü belirleyici birinin olduğu söylenir parabolik halinde
Belirli bir sabit nokta ile tüm parabolik Möbius dönüşümlerinin kümesi , özdeşlikle birlikte , matrisler grubuna eşbiçimli bir alt grup oluşturur.
karakteristik sabit
Tüm parabolik olmayan dönüşümlerin iki sabit noktası vardır ve bir matris eşleniği ile tanımlanır.
eliptik dönüşümler

Dönüşüm olduğu söylenir eliptik bir matris ile temsil edilebilir, eğer olan izidir gerçek ile
Bir dönüşüm, ancak ve ancak | λ | = 1 ve λ ≠ ±1. Yazma , eliptik bir dönüşüm eşleniğidir
Söz konusu Not bir karakteristik sabiti ile k , karakteristik sabit olan k , n . Bu nedenle, sonlu düzenin tüm Möbius dönüşümleri eliptik dönüşümlerdir, yani tam olarak λ'nın birliğin kökü olduğu veya eşdeğer olarak, α'nın π'nin rasyonel bir katı olduğu dönüşümlerdir . α = π / 2 kesirli çoklu ortalamanın en basit olasılığı , aynı zamanda 'nin benzersiz durumudur , aynı zamanda bir olarak ifade edilir. dairesel dönüşüm ; bu geometrik olarak iki sabit nokta etrafında 180° dönüşe karşılık gelir. Bu sınıf matris formunda şu şekilde temsil edilir:
hiperbolik dönüşümler
Transform is olduğu söylenen hiperbolik bir matris ile temsil edilebilir, eğer olan izidir
gerçek ileBir dönüşüm ancak ve ancak λ gerçek ve λ ≠ ±1 ise hiperboliktir .
loksodromik dönüşümler
[0,4]'te değilse dönüşümün loxodromic olduğu söylenir . Bir dönüşüm loxodromic ancak ve ancak .
Tarihsel olarak, navigasyon ile kerte hattı veya kerte hattının sabit bir yol anlamına gelir yatak ; sonuçta ortaya çıkan yol, bir loxodromic Möbius dönüşümünün yaptığı karmaşık düzlemin dönüşümlerine benzer şekilde logaritmik bir spiraldir . Aşağıdaki geometrik şekillere bakın.
Genel sınıflandırma
| dönüşüm | iz kare | çarpanlar | Sınıf temsilcisi | |
|---|---|---|---|---|
| dairesel | σ = 0 | k = -1 | z ↦ − z | |
| Eliptik | 0 ≤ σ < 4 | | k | = 1 | z ↦ e ben θ z | |
| Parabolik | σ = 4 | k = 1 | z ↦ z + bir | |
| hiperbolik | 4 < σ < ∞ | z ↦ e θ z | ||
| loksodromik | σ ∈ C \ [0,4] | z ↦ kz | ||
Gerçek durum ve terminoloji üzerine bir not
Gerçek sayılar üzerinde (katsayıların gerçek olması gerekiyorsa), hiperbolik olmayan loksodromik dönüşümler yoktur ve sınıflandırma, gerçek koniklerde olduğu gibi eliptik, parabolik ve hiperbolik olarak yapılır . Terminoloji, izin mutlak değerinin, |tr|/2'nin yarısının, dönüşümün eksantrikliği olarak kabul edilmesinden kaynaklanmaktadır - 2'ye bölme, boyut için düzeltir, dolayısıyla kimliğin eksantrikliği 1'e sahiptir (tr/ n bazen bir bu nedenle iz için alternatif) ve mutlak değer, PSL'de çalışma nedeniyle yalnızca ±1 faktörüne kadar tanımlanan iz için düzeltir. Alternatif olarak, yukarıda yapıldığı gibi , iz karesinin yarısı , eksantriklik karesi için bir vekil olarak kullanılabilir; bu sınıflandırmalar (ancak tam eksantriklik değerleri değil, çünkü kare alma ve mutlak değerler farklıdır) gerçek izler için uygundur, ancak karmaşık izler için değil. Aynı terminoloji SL(2, R ) (2 katlı kapak) elemanlarının sınıflandırılması için kullanılır ve
benzer sınıflandırmalar başka yerlerde kullanılır. Loxodromic dönüşümler esasen karmaşık bir fenomendir ve karmaşık eksantrikliklere karşılık gelir.Karakteristik sabitin geometrik yorumu
Aşağıdaki resim (küreden düzleme stereografik dönüşümden sonra) parabolik olmayan durumda bir Möbius dönüşümünün iki sabit noktasını göstermektedir:
Karakteristik sabit, logaritması cinsinden ifade edilebilir :
eliptik dönüşümler
Eğer ρ = 0, daha sonra sabit noktası ne çekici veya itici fakat ilgisiz ve dönüşüm olduğu söylenir eliptik . Bu dönüşümler, tüm noktaları iki sabit nokta etrafında daireler halinde hareket ettirme eğilimindedir. Sabit noktalardan biri sonsuzdaysa, bu bir nokta etrafında afin bir dönüş yapmaya eşdeğerdir.
Herhangi bir eliptik Möbius dönüşümü tarafından üretilen tek parametreli alt grubu alırsak, alt gruptaki her dönüşüm aynı iki noktayı sabitleyecek şekilde sürekli bir dönüşüm elde ederiz . Diğer tüm noktalar, Riemann küresi üzerindeki iki sabit nokta arasında yuvalanmış bir daire ailesi boyunca akar. Genel olarak, iki sabit nokta herhangi iki farklı nokta olabilir.
Bunun önemli bir fiziksel yorumu var. Bir gözlemcinin bir eksen etrafında sabit açısal hızla döndüğünü hayal edin. O zaman iki sabit noktayı gök küresinin Kuzey ve Güney kutupları olarak alabiliriz. Gece gökyüzünün görünümü, şimdi, 0, ∞ sabit noktalarını paylaşan ve gözlemcimizin sabit açısal hızına karşılık gelen α sayısı ile eliptik dönüşümlerin tek parametreli alt grubu tarafından tam olarak tarif edildiği şekilde sürekli olarak dönüştürülür.
Eliptik bir Möbius dönüşümünün Riemann küresi üzerindeki etkisini gösteren bazı şekiller (uçakta stereografik izdüşümünden sonra):
Bu resimler tek bir Möbius dönüşümünün etkisini göstermektedir. Oluşturduğu tek parametreli alt grup , resimlerin önerdiği dairesel yay ailesi boyunca noktaları sürekli hareket ettirir.
hiperbolik dönüşümler
Eğer α sıfır (ya da 2 katı olan tt ), transformasyon olduğu söylenir hiperbolik . Bu dönüşümler, noktaları dairesel yollar boyunca sabit bir noktadan diğerine doğru hareket ettirme eğilimindedir.
Herhangi bir hiperbolik Möbius dönüşümü tarafından üretilen tek parametreli alt grubu alırsak, alt gruptaki her dönüşüm aynı iki noktayı sabitleyecek şekilde sürekli bir dönüşüm elde ederiz . Diğer tüm noktalar , birinci sabit noktadan uzağa ve ikinci sabit noktaya doğru belirli bir dairesel yay ailesi boyunca akar . Genel olarak, iki sabit nokta, Riemann küresi üzerindeki herhangi iki farklı nokta olabilir.
Bunun da önemli bir fiziksel yorumu var. Bir gözlemcinin kendi gök küresi üzerinde Kuzey kutbu yönünde hızlandığını (sabit bir ivme ile) hayal edin. Daha sonra gece göğünün görünümü, 0, ∞ sabit noktalarını paylaşan hiperbolik dönüşümlerin tek parametreli alt grubu tarafından tam olarak tarif edildiği şekilde dönüştürülür, gerçek sayı ρ onun ivme vektörünün büyüklüğüne karşılık gelir. Yıldızlar, Güney kutbundan Kuzey kutbuna doğru boylamlar boyunca hareket ediyor gibi görünüyor. (Boylamlar, küreden düzleme stereografik izdüşüm altında dairesel yaylar olarak görünür.)
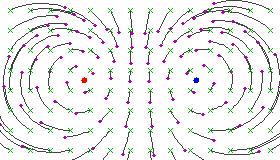
Hiperbolik bir Möbius dönüşümünün Riemann küresi üzerindeki etkisini gösteren bazı şekiller (uçakta stereografik izdüşümünden sonra):
Bu resimler, sabit noktalarda bulunan bir pozitif ve bir negatif elektrik yükünün alan çizgilerine benzer, çünkü dairesel akış çizgileri, iki sabit nokta arasında sabit bir açı oluşturur.
loksodromik dönüşümler
Eğer her iki ρ ve α sıfırdan farklı, transformasyon olduğu söylenir kerte hattında seyre . Bu dönüşümler, S-şekilli yollardaki tüm noktaları bir sabit noktadan diğerine taşıma eğilimindedir.
Kelime " kerte hattı ", λοξος (LOXOS): "Yunan dan çekik , + δρόμος (dromoslu) Tabii ". Ne zaman yelken sabit üzerinde rulman - (demek) kuzey-doğu arasında bir başlık sürdürmeleri halinde, sonunda etrafında yelken kadar rüzgar edecek kuzey kutbuna bir de logaritmik spiral . Açık kruger projeksiyonu kuzey ve güney kutupları sonsuza proje olarak böyle bir kurs, düz bir çizgidir. Loxodrome'un boylam çizgilerine göre gösterdiği açı (yani eğimi, spiralin "sıkılığı") k'nin argümanıdır . Tabii ki, Möbius dönüşümlerinin iki sabit noktası sadece kuzey ve güney kutuplarında değil, herhangi bir yerde olabilir. Ancak herhangi bir loxodromic dönüşüm, bu tür loxodromlar boyunca tüm noktaları hareket ettiren bir dönüşüme eşlenik olacaktır.
Herhangi bir loxodromic Möbius dönüşümü tarafından üretilen tek parametreli alt grubu alırsak,
alt gruptaki her dönüşüm aynı iki noktayı sabitleyecek şekilde sürekli bir dönüşüm elde ederiz . Diğer tüm noktalar , birinci sabit noktadan uzağa ve ikinci sabit noktaya doğru , belirli bir eğri ailesi boyunca akar . Hiperbolik durumdan farklı olarak, bu eğriler dairesel yaylar değil, küreden düzleme stereografik izdüşüm altında belirli eğriler, saat yönünün tersine sonsuz sıklıkla bir sabit nokta etrafında ve saat yönünde sonsuz sıklıkla diğer sabit nokta etrafında dönen spiral eğriler olarak görünür. Genel olarak, iki sabit nokta, Riemann küresi üzerindeki herhangi iki farklı nokta olabilir.İki sabit noktanın 0 olduğu durumdaki fiziksel yorumu muhtemelen tahmin edebilirsiniz, ∞: hem bir eksen etrafında dönen (sabit açısal hızla) hem de aynı eksen boyunca hareket eden bir gözlemci , gece gökyüzünün görünümünü görecektir. sırasıyla gerçek doğrusal ve açısal hızların büyüklüğü ile belirlenen 0, ∞ ve ρ, α sabit noktaları olan loxodromic dönüşümlerin tek parametreli alt grubuna göre dönüşüm.
stereografik izdüşüm
Bu görüntüler ,
Riemann küresi üzerine stereografik olarak yansıtılan Möbius dönüşümlerini göstermektedir . Özellikle, bir küre üzerine yansıtıldığında, sonsuzdaki sabit bir noktanın özel durumunun, sabit noktaların keyfi bir konumda bulunmasından farklı olmadığına dikkat edin.| Sonsuzlukta bir sabit nokta | ||
| Sabit noktalar taban tabana zıt | ||
| İsteğe bağlı bir konumda sabit noktalar | ||
Bir dönüşümü yineleme
Bir dönüşümün sabit noktaları γ
1 , γ 2 ve karakteristik sabit k varsa , olacaktır .Bu, bir dönüşümü yinelemek veya bir dönüşümü adımlara bölerek canlandırmak için kullanılabilir .
Bu görüntüler, çeşitli karakteristik sabitlerle dönüşümler altında sürekli olarak yinelenen üç noktayı (kırmızı, mavi ve siyah) göstermektedir.
 |
 |
 |
|
Ve bu görüntüler, bir daireyi Hiperbolik, Eliptik ve Loksodromik dönüşümler altında dönüştürdüğünüzde ne olduğunu gösterir. Eliptik ve loxodromic görüntülerde α değerinin 1/10 olduğuna dikkat edin.
Daha yüksek boyutlar
Daha yüksek boyutta, bir Möbiüs dönüşümü a, homeomorfizma arasında ,
tek nokta kompaktifikasyonunun arasında sınırlı bir bileşimdir, alanda inversiyon ve yansımaları olarak hiperdüzlemleri . Uygun geometrideki Liouville teoremi, en az üç boyutta tüm uyumlu dönüşümlerin Möbius dönüşümleri olduğunu belirtir . Her Möbius dönüşümü forma konabilirburada , , bir
ortogonal matristir ve 0 veya 2'dir. Möbius dönüşümleri grubuna Möbius grubu da denir .Yönlendirmeyi koruyan Möbius dönüşümleri, Möbius grubundaki kimliğin bağlantılı bileşenini oluşturur. n = 2 boyutunda , oryantasyonu koruyan Möbius dönüşümleri tam olarak burada kapsanan Riemann küresinin haritalarıdır. Yönü tersine çevirenler, bunlardan karmaşık konjugasyonla elde edilir.
Möbius dönüşümlerinin alanı, yani ,
n -boyutlu küreye homeomorfiktir . Bu iki uzay arasındaki kanonik eşbiçimlilik , kendisi de bir Möbius dönüşümü olan Cayley dönüşümüdür . Bu tanımlama, Möbius dönüşümlerinin aynı zamanda . N -sphere birlikte Möbiüs grubu aksiyonu ile, (Klein anlamında bir geometrik yapı Erlangen programı olarak adlandırılır) Möbiüs geometrisi .Uygulamalar
Lorentz dönüşümü
Möbius grubunun Lorentz grubu ile bir izomorfizmi birkaç yazar tarafından not edilmiştir: Felix Klein'ın (1893, 1897) hiperbolik geometri ve Möbius geometrisi ile ilgili otomorfik fonksiyonlar üzerine önceki çalışmasına dayanarak , Gustav Herglotz (1909), hiperbolik hareketlerin (yani Bir
hiperbolik uzayın izometrik otomorfizmaları ) birim küreyi kendisine dönüştüren Lorentz dönüşümlerine karşılık gelir, bu sayede Herglotz tek parametreli Lorentz dönüşümlerini loxodromik, eliptik, hiperbolik ve parabolik gruplara sınıflandırabilir. Diğer yazarlar arasında Emil Artin (1957), HSM Coxeter (1965) ve Roger Penrose , Wolfgang Rindler (1984), Tristan Needham (1997) ve WM Olivia (2002) bulunmaktadır.Minkowski uzayı alanı koordinat dört boyutlu gerçek oluşur R 4 (sıralı dörtgen alanı kapsayan X 0 , x 1 , x 2 , x 3 birlikte bir ile birlikte) gerçek sayılar, ikinci dereceden formu
Özel görelilikten ödünç alınan terminoloji, Q > 0 olan noktalar zamana benzer olarak kabul edilir ; ek olarak, eğer x 0 > 0 ise , bu noktaya geleceğe dönük denir . İle Nokta Q <0 denir spacelike . Boş koni S bu noktalarda oluşan S = 0 ; gelecek boş koni K + boş koni ile ilgili noktalardır x 0 > 0 . Gökküre sonra ışınların toplama tanımlanan K + Başlangıç noktası kökeni R 4 . Toplanması lineer dönüşümler ile R 4 pozitif olan belirleyici ikinci dereceden bir şekilde korunması Q ve zaman yönü formu koruyarak sınırlı Lorentz grubu SO + (1,3).
Göksel kürenin geometrisi ile bağlantılı olarak, SO + (1,3) dönüşümleri grubu , kürenin Möbius dönüşümlerinin PSL(2, C ) grubuyla tanımlanır . Her ( x 0 , x 1 , x 2 , x 3 ) ∈ R 4 için
hermit matrisini ilişkilendirinBelirleyici matris X eşittir Q ( x 0 , x 1 , x 2 , x 3 ) . Özel lineer grubu tür matrislerin boşluk yoluyla etki eder
-
( 1 )
her biri için bir ∈ SL (2, Cı- ) ve SL bu işlem (2, C ) determinantını korur X için det bir = 1 . X'in determinantı ikinci dereceden Q formu ile tanımlandığından , SL(2, C ) Lorentz dönüşümleri ile etki eder. Boyutsal olarak, SL(2, C ), SO(1,3) kimliğinin bir komşuluğunu kapsar. SL(2, C ) bağlı olduğundan, tüm kısıtlı Lorentz grubu SO + (1,3)' ü kapsar . Ayrıca, (
1 ) eyleminin çekirdeği {± I } alt grubu olduğundan, bölüm grubuna geçmek grup izomorfizmini verir.-
( 2 )
Şimdi dikkati ( x 0 , x 1 , x 2 , x 3 ) null olduğu duruma odaklayarak, X matrisinin sıfır determinantı vardır ve bu nedenle karmaşık iki vektörlü ξ karmaşık eşleniğinin dış çarpımı olarak bölünür :
-
( 3 )
İki bileşenli vektör ξ, (
1 ) ile uyumlu bir şekilde SL(2, C ) tarafından etkilenir . Artık SL(2, C )'nin hermit matrisleri üzerindeki temsilinin çekirdeğinin {± I } olduğu açıktır .PSL(2, C )'nin göksel küre üzerindeki etkisi, stereografik izdüşüm kullanılarak geometrik olarak da tanımlanabilir . İlk olarak,
x 0 = 1 ile verilen R 4'teki hiperdüzlemi ele alalım . Göksel küre , hiperdüzlemin gelecekteki boş koni N + ile kesiştiği küre S + ile tanımlanabilir . Bu kürenin kuzey kutbundan (1,0,0,1) x 3 = 0 düzlemine stereografik izdüşüm, koordinatları (1, x 1 , x 2 , x 3 ) olan bir nokta alır.Karmaşık koordinatın tanıtılması
-
( 4 )
SO eylem + noktalarına ile (1,3) , N + altdüzlem korumaz S + , ama nokta üzerine etki S + ve sonra sonuç olarak yeniden böylece yeniden ölçeklendirme S + SO bir etki verir + ( 1,3) karmaşık değişken ζ üzerinde bir eyleme geçen küre üzerinde. Aslında, bu eylem, göksel kürenin bu temsilinden kolayca görülmese de, kesirli doğrusal dönüşümlerle gerçekleşir. Tersine, ζ değişkeninin herhangi bir kesirli lineer dönüşümü için , muhtemelen uygun (benzersiz olarak belirlenmiş) bir yeniden ölçeklendirmeden sonra N + üzerinde benzersiz bir Lorentz dönüşümüne geçer .
İşlem daha açık bir şekilde görülebilir sağlar stereografik çıkıntının daha değişmez açıklama değişken ζ = göz önünde bulundurulması gereken z : ağırlık karmaşık yansıtmalı hattı için homojen koordinatlarla, bir çift bir oranı olarak CP 1 . Stereografik izdüşüm , gerçek ölçeklere göre ikinci dereceden homojen olan C 2 − {0}'den N + ' ya bir dönüşüme gider.
-
( 5 )
(
5 ) ' in bileşenlerinin tam olarak dış üründen elde edilenler olduğu ölçeklerle kısıtlama konusunda ( 4 ) ile aynı fikirde olanÖzetle, kısıtlı Lorentz grubu SO + (1,3)' ün eylemi , Möbius grubu PSL(2, C ) ile uyumludur . Bu, aşağıdaki tanımı motive eder. Boyutta N ≥ 2, Möbiüs grubu Mob ( n ) her yönlendirme koruyucu grubudur konformal izometrileri yuvarlak küre S , n kendisine. Uyumlu küreyi Minkowski uzayı R 1,n+1 ' de sıfır koninin geleceğe dönük ışınlarının uzayı olarak gerçekleştirerek, Möb( n )'nin sınırlı Lorentz grubu SO + (1, n +1 ) ile bir izomorfizmi vardır. ) pozitif determinant ile Lorentz dönüşümlerinin, zamanın yönünü koruyarak.
Coxeter bunun yerine eşdeğer ikinci dereceden formla başladı
Lorentz grubunu { x : Q( x ) = -1}'in kararlı olduğu dönüşümlerle tanımladı . Sonra x'leri homojen koordinatlar olarak ve { x : Q( x ) = 0} sıfır konisini {
x : Q( x ) < 0} noktalarından oluşan hiperbolik uzay için Cayley mutlakı olarak yorumladı . Daha sonra, Coxeter değişkenleri tanıttıöyle ki Lorentz-değişmez kuadranı küreye karşılık gelir Coxeter,
Felix Klein'ın (0, 0, 1)'den karmaşık düzleme stereografik izdüşüm uygulayarak bu yazışma hakkında yazdığını not eder. hiperbolik uzay ve genel homografi, iki veya dört düzlemdeki inversiyonların ürünü olan genel hiperbolik yer değiştirmeye tekabül eden iki veya dört daire içindeki inversiyonların ürünüdür.hiperbolik uzay
Yukarıda görüldüğü gibi, Möbius grubu PSL(2, C ) Minkowski uzayı üzerinde orijini, uzayın yönelimini ve zamanın yönünü koruyan izometrilerin grubu olarak etki eder. Noktalarına kısıtlama S bir modelini oluşturur = pozitif ışık konisi 1, hiperbolik 3-uzay H 3 biz Möbiüs grubu üzerinde etkili olduğunu görmek H 3 yönlendirme koruyucu izometrileri bir grup olarak. Aslında, Möbius grubu, hiperbolik 3-uzaylı yönelimi koruyan izometriler grubuna eşittir.
Kullandığımız Eğer Poincaré top modeli içinde birim topu tanımlayarak, R 3 ile H 3 , o zaman bir "konformal sınır" olarak Riemann küresinin düşünebiliriz H 3 . Her yönlendirme koruyucu izometri H 3 Riemann küre ve tersi bir Möbiüs dönüşüme yol açar; bu, fizikte AdS/CFT yazışma varsayımlarına yol açan ilk gözlemdir .
Ayrıca bakınız
- çift doğrusal dönüşüm
- konformal geometri
- Fuşya grubu
- genelleştirilmiş daire
- hiperbolik geometri
- Analitik fonksiyonların sonsuz bileşimleri
- inversiyon dönüşümü
- Kleinyen grubu
- Yalan küre geometrisi
- Doğrusal kesirli dönüşüm
- Liouville teoremi (uyumlu eşlemeler)
- Lorentz grubu
- Modüler grup
- Poincare yarım düzlem modeli
- projektif geometri
- Bir halka üzerinde yansıtmalı çizgi
- Lorentz grubunun temsil teorisi
Notlar
Referanslar
Özel
Genel
- Arnold, Douglas N.; Rogness, Jonathan (2008), "Möbius Dönüşümleri Açığa Çıktı" (PDF) , AMS Bildirimleri , 55 (10): 1226–1231
- Beardon, Alan F. (1995), Ayrık Grupların Geometrisi , New York: Springer-Verlag, ISBN 978-0-387-90788-8
- Hall, GS (2004), Genel Relativitede Simetriler ve Eğrilik Yapısı , Singapur: World Scientific, ISBN 978-981-02-1051-9 (Lorentz grubunun Lie cebirinin Lie alt cebirlerinin eşlenikliğe kadar sınıflandırılması için Bölüm 6'ya bakınız.)
- Katok, Svetlana (1992), Fuşya Grupları , Chicago: Chicago Press Üniversitesi, ISBN 978-0-226-42583-2 Bölüm 2'ye bakın .
- Klein, Felix (1888), İkosahedron üzerine dersler ve beşinci dereceden denklemlerin çözümü (Dover ed.), ISBN 978-0-486-49528-6.
- Knopp, Konrad (1952), Fonksiyonlar Teorisinin Elemanları , New York: Dover, ISBN 978-0-486-60154-0 (Riemann küresi, stereografik izdüşüm ve Möbius dönüşümlerine güzel bir giriş için bu klasik kitabın 3-5. Bölümlerine bakın.)
- Mumford, David ; Dizi, Caroline; Wright, David (2002), Indra'nın İncileri: Felix Klein'ın Vizyonu , Cambridge University Press, ISBN 978-0-521-35253-6 (Matematikçi olmayanlara yöneliktir, şemalarla zengin bir şekilde gösterilen teori ve sonuçların mükemmel bir açıklamasını sağlar.)
- Needham, Tristan (1997), Görsel Kompleks Analizi , Oxford: Clarendon Press, ISBN 978-0-19-853446-4 (Möbius dönüşümlerine, eşlenikliğe kadar sınıflandırmaları da dahil olmak üzere, güzel bir şekilde resimlendirilmiş bir giriş için Bölüm 3'e bakın.)
- Penrose, Roger ; Rindler, Wolfgang (1984), Spinörler ve uzay-zaman, Cilt 1: İki spinli hesap ve göreli alanlar , Cambridge University Press, ISBN 978-0-521-24527-2
- Schwerdtfeger, Hans (1979), Karmaşık Sayıların Geometrisi , Dover, ISBN 978-0-486-63830-0 (Möbius dönüşümlerine giriş için Bölüm 2'ye bakın.)
- Tóth, Gábor (2002), Sonlu Möbius grupları, kürelerin minimal daldırmaları ve modüller
daha fazla okuma
- Lawson, OG (1998). "Möbius Ters Monoid" . Cebir Dergisi . 200 (2): 428. doi : 10.1006/jabr.1997.7242 .
Dış bağlantılar
-
 İlgili Medya Möbius dönüşümü Wikimedia Commons
İlgili Medya Möbius dönüşümü Wikimedia Commons - "Yarı-konformal haritalama" , Matematik Ansiklopedisi , EMS Press , 2001 [1994]
- Uygun haritalar galerisi
- Weisstein, Eric W. "Doğrusal Kesirli Dönüşüm" . Matematik Dünyası .





































































![{\displaystyle [z_{1}:z_{2}]\ \thicksim [z_{1}/z_{2},\ 1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfde0106eeb65683fa6aa517246aab4c2b9360e6)

![{\displaystyle [z,\ 1]{\begin{pmatrix}a&c\\b&d\end{pmatrix}}\ =\ [az+b,\ cz+d]\ =\ \left[{\frac {az+ b}{cz+d}},\ 1\sağ]\ =\ f(z).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/33b8bbc7be964b3996e15687779dfbf71f4c3bdd)