Karnaugh haritası - Karnaugh map

Örnek bir Karnaugh haritası. Fonksiyon için: Bu resim aslında iki Karnaugh haritaları gösteren ƒ kullanarak mintermleri (renkli dikdörtgenler) ve onun tamamlayıcı için, kullanan maxtermler (gri dikdörtgenler). Resimde, E (), makalede olarak gösterilen mintermlerin toplamını ifade eder .${\displaystyle \sum m_{i}}$

Karnaugh haritası ( KM veya K-haritası ) basitleştirilmesi yöntemidir Boole cebri ifadeleri. Maurice Karnaugh , 1953'te , Allan Marquand'ın 1881 mantıksal diyagramının ( diğer bir deyişle Marquand diyagramının) yeniden keşfi olan Edward W. Veitch'in 1952 Veitch şemasının bir iyileştirmesi olarak tanıttı , ancak şimdi devreleri değiştirmek için kullanımına odaklandı. Veitch çizelgeleri bu nedenle Marquand-Veitch diyagramları olarak ve Karnaugh haritaları Karnaugh-Veitch haritaları ( KV haritaları ) olarak da bilinir .

Karnaugh haritası, insanların örüntü tanıma yeteneğinden yararlanarak kapsamlı hesaplama ihtiyacını azaltır. Ayrıca potansiyel yarış koşullarının hızlı bir şekilde tanımlanmasına ve ortadan kaldırılmasına izin verir .

Gerekli Boole sonuçları bir doğruluk tablosundan iki boyutlu bir ızgaraya aktarılır, burada Karnaugh haritalarında hücreler Gray kodunda sıralanır ve her hücre konumu giriş koşullarının bir kombinasyonunu temsil eder. Hücreler ayrıca mintermler olarak da bilinir, her hücre değeri boole işlevinin karşılık gelen çıkış değerini temsil eder. Orijinal doğruluk tablosundaki mantığın kanonik formunun terimlerini temsil eden 1'ler veya 0'lardan oluşan en uygun gruplar belirlenir . Bu terimler, gerekli mantığı temsil eden minimal bir Boole ifadesi yazmak için kullanılabilir.

Karnaugh haritaları, minimum sayıda mantık kapısı kullanılarak uygulanabilmeleri için gerçek dünyadaki mantık gereksinimlerini basitleştirmek için kullanılır. Bir sum of ürünleri ifadesi (SOP) her zaman kullanılarak uygulanabilir ve kapılar , bir besleyen OR kapısının bir ve ürün-of-toplamları ekspresyonu (POS) neden olduğu veya bir VE kapısı besleme kapıları. POS ifadesi, fonksiyonun bir tamamlayıcısını verir (eğer F fonksiyon ise, tamamlayıcısı F' olacaktır). Karnaugh haritaları, yazılım tasarımında mantıksal ifadeleri basitleştirmek için de kullanılabilir. Boolean koşulları, örneğin koşullu ifadelerde kullanıldığı gibi , çok karmaşık hale gelebilir ve bu da kodun okunmasını ve korunmasını zorlaştırır. Küçültüldükten sonra, kurallı toplamlar ve toplamlar çarpımı ifadeleri, AND ve OR mantık operatörleri kullanılarak doğrudan uygulanabilir.

Örnek

Karnaugh haritaları, Boolean cebir fonksiyonlarının basitleştirilmesini kolaylaştırmak için kullanılır . Örneğin, aşağıdaki doğruluk tablosunda açıklanan Boole işlevini düşünün .

Bir fonksiyonun doğruluk tablosu

	A	B	C	NS	${\görüntüleme stili f(A,B,C,D)}$
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

Aşağıda, A , B , C , D Boole değişkenlerini ve bunların tersini kullanarak, basitleştirilmemiş Boole cebirinde aynı işlevi açıklayan iki farklı gösterim verilmiştir .

• ${\displaystyle f(A,B,C,D)=\sum _{}m_{i},i\in \{6,8,9,10,11,12,13,14\}}$nerede olduğu mintermler haritaya (yani doğruluk tablosunda çıkışı 1 var satırlar).${\displaystyle m_{i}}$
• ${\displaystyle f(A,B,C,D)=\prod _{}M_{i},i\in \{0,1,2,3,4,5,7,15\}}$nerede olduğu maxtermler haritaya (yani doğruluk tablosundaki çıkışı 0 sahip satırlar).${\displaystyle M_{i}}$

Bir simit üzerinde ve bir düzlemde çizilmiş K-haritası. Nokta işaretli hücreler bitişiktir.

K-haritası yapımı. Çıkış değerleri (doğruluk tablosundaki en sağdaki değerler) yerine bu diyagram, ABCD girişinin (doğruluk tablosundaki en soldaki değerler) ondalık gösterimini gösterir, bu nedenle bir Karnaugh haritası değildir.

Üç boyutta, bir dikdörtgen bir torus şeklinde bükülebilir.

Yapı

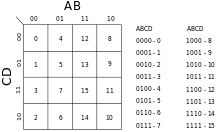
Yukarıdaki örnekte, dört girdi değişkeni 16 farklı şekilde birleştirilebilir, dolayısıyla doğruluk tablosunun 16 satırı ve Karnaugh haritasının 16 konumu vardır. Karnaugh haritası bu nedenle 4 × 4 ızgara şeklinde düzenlenmiştir.

Satır ve sütun endeksleri (Karnaugh haritasının üst ve sol tarafında gösterilir) ikili sayısal sıra yerine Gray kodunda sıralanır. Gri kod, her bir bitişik hücre çifti arasında yalnızca bir değişkenin değişmesini sağlar. Tamamlanan Karnaugh haritasının her hücresi, bu girdi kombinasyonu için fonksiyonun çıktısını temsil eden bir ikili rakam içerir.

gruplama

Karnaugh haritası oluşturulduktan sonra, doğruluk tablosundaki bilgiler için mümkün olan en basit formlardan birini ( kanonik bir form) bulmak için kullanılır . Karnaugh haritasındaki bitişik 1'ler, ifadeyi basitleştirme fırsatlarını temsil eder. Son ifade için mintermler ('minimal terimler'), haritada 1'li grupların çevrelenmesiyle bulunur. Minterm grupları dikdörtgen olmalı ve iki katı olan bir alana sahip olmalıdır (yani, 1, 2, 4, 8...). Minterm dikdörtgenler, 0'lar içermeden mümkün olduğunca büyük olmalıdır. Gruplar, her birini büyütmek için üst üste gelebilir. Aşağıdaki örnekteki optimal gruplamalar yeşil, kırmızı ve mavi çizgilerle işaretlenmiştir ve kırmızı ve yeşil gruplar örtüşmektedir. Kırmızı grup 2 × 2 karedir, yeşil grup 4 × 1 dikdörtgendir ve örtüşen alan kahverengi ile gösterilir.

Hücreler genellikle, hücrenin kapsadığı girişlerin mantıksal değerini tanımlayan bir kısayol ile gösterilir. Örneğin AD , A ve D' nin doğru olduğu 2x2'lik alanı , yani yukarıdaki diyagramda 13, 9, 15, 11 numaralı hücreleri kapsayan bir hücre anlamına gelir . Öte yandan, bir D hücreleri anlamına gelecektir bir doğrudur ve D (olduğu yanlış, D geçerlidir).

Izgara, toroidal olarak bağlanmıştır, bu, dikdörtgen grupların kenarlar boyunca sarılabileceği anlamına gelir (resme bakın). En sağdaki hücreler, karşılık gelen giriş değerlerinin yalnızca bir bit farklı olması anlamında, en soldaki hücrelere aslında 'bitişik'tir; Benzer şekilde, en üsttekiler ve alttakiler de öyle. Bu nedenle, bir D olabilir geçerli bir dönem olduğu gibi 14-hücreleri 10 ve dahil alt hücreleri 12 ve üst 8 ve sargıları kapsamaktadır B D , dört köşe içerir.

Çözüm

İki K-haritasını gösteren diyagram. f(A, B, C, D) fonksiyonunun K-haritası mintermlere karşılık gelen renkli dikdörtgenler olarak gösterilir. Kahverengi bölge, kırmızı 2×2 kare ile yeşil 4×1 dikdörtgenin örtüşmesidir. f'nin tersi için K-haritası, maksimum terimlere karşılık gelen gri dikdörtgenler olarak gösterilir.

Karnaugh haritası oluşturulduktan ve bitişik 1'ler dikdörtgen ve kare kutularla bağlandıktan sonra, her kutuda hangi değişkenlerin aynı kaldığı incelenerek cebirsel mintermler bulunabilir.

Kırmızı gruplama için:

• A , kutu boyunca aynıdır ve 1'e eşittir, bu nedenle kırmızı mintermin cebirsel gösterimine dahil edilmelidir.
• B aynı durumu korumaz (1'den 0'a geçer) ve bu nedenle hariç tutulmalıdır.
• C değişmez. Her zaman 0'dır, bu nedenle tamamlayıcısı NOT-C dahil edilmelidir. Bu nedenle, C dahil edilmelidir.
• D değişir, bu nedenle hariç tutulur.

Böylece Boole sum of ürünler ifadesi ilk Minterm olan bir Cı .

Yeşil gruplama için, A ve B aynı durumu korurken, C ve D değişir. B , 0'dır ve dahil edilmeden önce olumsuzlanması gerekir. Dolayısıyla ikinci terim A B'dir . Yeşil gruplamanın kırmızı grupla örtüşmesinin kabul edilebilir olduğunu unutmayın.

Aynı şekilde mavi gruplandırma BC D terimini verir .

Her gruplamanın çözümleri birleştirilir: devrenin normal şekli . ${\displaystyle A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}}$

Böylece Karnaugh haritası, basitleştirmeye rehberlik etti.

${\displaystyle {\begin{aligned}f(A,B,C,D)={}&{\overline {A}}BC{\overline {D}}+A{\overline {B}}\,{ \overline {C}}\,{\overline {D}}+A{\overline {B}}\,{\overline {C}}D+A{\overline {B}}C{\overline {D} }+{}\\&A{\overline {B}}CD+AB{\overline {C}}\,{\overline {D}}+AB{\overline {C}}D+ABC{\overline {D }}\\={}&A{\overline {C}}+A{\overline {B}}+BC{\overline {D}}\end{hizalı}}}$

Boole cebrinin aksiyomlarını dikkatli bir şekilde uygulayarak bu basitleştirmeyi elde etmek mümkün olabilirdi , ancak bunu yapmak için gereken süre terimlerin sayısıyla katlanarak artar.

Ters

Bir fonksiyonun tersi, bunun yerine 0'ları gruplayarak aynı şekilde çözülür.

Tersini kapsayan üç terimin tümü, farklı renkli kenarlıklara sahip gri kutularla gösterilmiştir:

• kahverengi : A B
• altın : A C
• mavi : BCD

Bu, tersini verir:

${\displaystyle {\overline {f(A,B,C,D)}}={\overline {A}}\,{\overline {B}}+{\overline {A}}\,{\overline { C}}+BCD}$

Kullanımı sayesinde De Morgan yasaları , toplamlar ürünü tespit edilebilir:

${\displaystyle {\begin{aligned}f(A,B,C,D)&={\overline {\overline {f(A,B,C,D)}}}\\&={\overline {{ \overline {A}}\,{\overline {B}}+{\overline {A}}\,{\overline {C}}+BCD}}\\&=\left({\overline {{\overline {A}}\,{\overline {B}}}}\sağ)\left({\overline {{\overline {A}}}\,{\overline {C}}}}\right)\sol({ \overline {BCD}}\sağ)\\&=\sol(A+B\sağ)\sol(A+C\sağ)\left({\overline {B}}+{\overline {C}}+ {\overline {D}}\sağ)\end{hizalı}}}$

umrumda değil

ABCD = 1111 için değeri "umurumda değil" ile değiştirilir. Bu, yeşil terimi tamamen kaldırır ve kırmızı terimin daha büyük olmasını sağlar. Ayrıca mavi ters terimin kaymasına ve büyümesine izin verir.${\görüntüleme stili f(A,B,C,D)}$

Karnaugh haritaları ayrıca doğruluk tabloları " umurumda değil " koşullarını içeren işlevlerin daha kolay minimizasyonuna izin verir . "Umurumda değil" koşulu, tasarımcının çıktının ne olduğunu umursamadığı girdilerin birleşimidir. Bu nedenle, "umurumda değil" koşulları, hangisi onu daha büyük yaparsa, herhangi bir dikdörtgen gruba dahil edilebilir veya hariç tutulabilir. Genellikle haritada bir tire veya X ile gösterilirler.

Sağdaki örnek, yukarıdaki örnekle aynıdır, ancak f (1,1,1,1) değeri "umurumda değil" ile değiştirilmiştir. Bu, kırmızı terimin sonuna kadar genişlemesine izin verir ve böylece yeşil terimi tamamen kaldırır.

Bu, yeni minimum denklemi verir:

${\displaystyle f(A,B,C,D)=A+BC{\overline {D}}}$

İlk terim sadece olduğunu Not A , değil A C . Bu durumda, umurumda olmayan bir terim düştü (yeşil dikdörtgen); basitleştirilmiş başka (kırmızı olan); ve yarış tehlikesini kaldırdı (aşağıdaki yarış tehlikeleri bölümünde gösterildiği gibi sarı terimin kaldırılması).

Ters durum aşağıdaki gibi basitleştirilmiştir:

${\displaystyle {\overline {f(A,B,C,D)}}={\overline {A}}\,{\overline {B}}+{\overline {A}}\,{\overline { C}}+{\overline {A}}D}$

Kullanımı sayesinde De Morgan yasaları , toplamlar ürünü tespit edilebilir:

${\displaystyle {\begin{aligned}f(A,B,C,D)&={\overline {\overline {f(A,B,C,D)}}}\\&={\overline {{ \overline {A}}\,{\overline {B}}+{\overline {A}}\,{\overline {C}}+{\overline {A}}\,D}}\\&=\ left({\overline {{\overline {A}}\,{\overline {B}}}}}\right)\left({\overline {{\overline {A}}}\,{\overline {C}}) }}\sağ)\sol({\üst çizgi {{\üst çizgi {A}}\,D}}\sağ)\\&=\sol(A+B\sağ)\sol(A+C\sağ)\ sol(A+{\overline {D}}\sağ)\end{hizalı}}}$

Yarış tehlikeleri

Eliminasyon

Karnaugh haritaları, yarış koşullarını tespit etmek ve ortadan kaldırmak için kullanışlıdır . Bir Karnaugh haritası kullanarak yarış tehlikelerini tespit etmek çok kolaydır, çünkü harita üzerinde sınırlandırılmış herhangi bir bitişik, ancak ayrık bölge arasında hareket ederken bir yarış durumu mevcut olabilir. Ancak, Gri kodlamanın doğası gereği, bitişik , yukarıda açıklanan özel bir tanıma sahiptir - aslında bir dikdörtgen yerine bir simit üzerinde hareket ediyoruz, üst, alt ve yanları sarıyoruz.

• Yukarıdaki örnekte , C 1 ve D 0, A 1 ve B 1'den 0'a değiştiğinde (mavi durumdan yeşil duruma geçerken) potansiyel bir yarış durumu mevcuttur . Bu durumda, çıktı 1'de değişmeden kalacak şekilde tanımlanır, ancak bu geçiş denklemde belirli bir terim tarafından kapsanmadığından, bir aksaklık potansiyeli (çıktının 0'a anlık geçişi) mevcuttur.
• Aynı örnekte, tespit edilmesi daha zor olan ikinci bir potansiyel aksaklık vardır: D 0 olduğunda ve A ve B'nin her ikisi de 1 olduğunda, C 1'den 0'a değişir (mavi durumdan kırmızı duruma geçer). Bu durumda aksaklık, haritanın üstünden altına doğru sarılır.

Bu şemada yarış tehlikeleri mevcuttur.

Yarış tehlikelerini önlemek için konsensüs terimlerinin eklendiği yukarıdaki diyagram.

Hataların gerçekten oluşup oluşmayacağı, uygulamanın fiziksel doğasına bağlıdır ve bunun için endişelenmemiz gerekip gerekmediği uygulamaya bağlıdır. Saatli mantıkta, zamanlama terminini karşılamak için mantığın zaman içinde istenen değere oturması yeterlidir. Örneğimizde, saatli mantığı düşünmüyoruz.

Bizim durumumuzda, ek bir terim , yeşil ve mavi çıkış durumları veya mavi ve kırmızı çıkış durumları arasında köprü kurarak potansiyel yarış tehlikesini ortadan kaldırır: bu sarı bölge olarak gösterilir (sağ alttan üste doğru sarılır). yarısı) bitişik diyagramda. ${\displaystyle A{\overline {D}}}$

Terim, sistemin statik mantığı açısından gereksizdir , ancak bu tür fazlalık veya fikir birliği terimlerine , yarışsız dinamik performansı sağlamak için sıklıkla ihtiyaç duyulur.

Benzer şekilde, başka bir potansiyel yarış tehlikesini ortadan kaldırmak için tersine ek bir terim eklenmelidir. De Morgan yasalarını uygulamak, f için başka bir toplamlar ifadesinin çarpımını yaratır , ancak yeni bir . ${\displaystyle {\overline {A}}D}$${\displaystyle \sol(A+{\overline {D}}\sağ)}$

2 değişkenli harita örnekleri

Aşağıdakiler tüm olası 2 değişkenli, 2 × 2 Karnaugh haritalarıdır. Bir fonksiyonu olarak mintermler her biriyle olan Listelenen ve yarış tehlike azade ( bkz önceki bölüm asgari denklemi). Minterm, eşlenen değişkenlerin en minimal ifade biçimini veren bir ifade olarak tanımlanır. Tüm olası yatay ve dikey birbirine bağlı bloklar oluşturulabilir. Bu bloklar 2'nin (1, 2, 4, 8, 16, 32, ...) kuvvetlerinin büyüklüğünde olmalıdır. Bu ifadeler, eşlenecek ikili ifadeler için minimum mantıksal değişken ifadelerinin minimum mantıksal eşlemesini oluşturur. İşte bir alana sahip tüm bloklar. ${\görüntüleme stili \toplam m()}$

Grafiğin altında, üstünde, solunda veya sağında bir blok devam ettirilebilir. Bu, değişken minimizasyon için grafiğin kenarının ötesine bile geçebilir. Bunun nedeni, her bir mantık değişkeninin her bir dikey sütuna ve yatay satıra karşılık gelmesidir. K-haritasının görselleştirilmesi silindirik olarak kabul edilebilir. Sol ve sağ kenarlardaki alanlar bitişik, üst ve alt alanlar bitişiktir. Dört değişken için K-Haritaları bir halka veya torus şekli olarak gösterilmelidir. K-haritasının çizdiği karenin dört köşesi bitişiktir. 5 değişken ve daha fazlası için hala daha karmaşık haritalara ihtiyaç vardır.

• 

  Σ m (0); K = 0

• 

  Σ m (1); K = A ′ B ′

• 

  Σ m (2); K = AB ′

• 

  Σ m (3); K = A ′ B

• 

  Σ m (4); K = AB

• 

  Σ m (1,2); K = B '

• 

  Σ m (1,3); K = A '

• 

  Σ m (1,4); K = A ′ B ′ + AB

• 

  Σ m (2,3); K = AB ′ + A ′ B

• 

  Σ m (2,4); K = A

• 

  Σ m (3,4); K = B

• 

  Σ m (1,2,3); K = A' + B '

• 

  Σ m (1,2,4); K = A + B '

• 

  Σ m (1,3,4); K = A ′ + B

• 

  Σ m (2,3,4); K = A + B

• 

  8 m (1,2,3,4); K = 1

İlgili grafik yöntemler

İlgili grafik küçültme yöntemleri şunları içerir:

• Allan Marquand (1853–1924) tarafından Marquand diyagramı (1881 )
• Veitch tablosu (1952) Edward W. Veitch tarafından (1924–2013)
• Mahoney haritası ( M-haritası , atama numaraları , 1963) Matthew V. Mahoney tarafından (daha fazla sayıda girdi için Karnaugh haritalarının yansıma-simetrik bir uzantısı)
• Seyrek değişkenler , harita girişli değişkenler (MEV), değişken girişli harita (VEM) veya değişken girişli Karnaugh haritası (VEKM)gibi azaltılmış Karnaugh haritası (RKM) teknikleri (1969'dan)GW Schultz, Thomas E. Osborne , Christopher R Clare, J. Robert Burgoon, Larry L. Dornhoff, William I. Fletcher, Ali M. Rushdi ve diğerleri (daha fazla sayıda girdi için değişken girdilere dayalı birkaç ardışık Karnaugh harita uzantısı)
• Minterm-halka haritası (MRM, 1990) Thomas R. McCalla (daha fazla sayıda girdi için Karnaugh haritalarının üç boyutlu bir uzantısı)

Ayrıca bakınız

• Cebirsel normal form (ANF)
• İkili karar diyagramı (BDD), bir Boole fonksiyonunun sıkıştırılmış bir temsili olan bir veri yapısı
• Espresso buluşsal mantık küçültücü
• Boole cebri konularının listesi
• Mantık optimizasyonu
• Punnett karesi (1905), biyolojide benzer bir diyagram
• Quine–McCluskey algoritması
• Reed-Müller genişlemesi
• Venn şeması (1880)
• Zhegalkin polinomu

Notlar

Referanslar

daha fazla okuma

• Katz, Randy Howard (1998) [1994]. Çağdaş Mantık Tasarımı . Benjamin/Cummings Yayıncılık Şirketi . s.  70–85 . doi : 10.1016/0026-2692(95)90052-7 . ISBN'si 0-8053-2703-7.
• Vingron, Şimon Peter (2004) [2003-11-05]. "Karnaugh Haritaları". Anahtarlama Teorisi: Yüklem Mantığı Yoluyla İçgörü . Berlin, Heidelberg, New York: Springer-Verlag . s. 57-76. ISBN'si 3-540-40343-4.
• Wickes, William E. (1968). "3.5. Veitch Diyagramları". Entegre Devrelerle Lojik Tasarım . New York, ABD: John Wiley & Sons . s.  36-49 . LCCN  68-21185 . P. 36: […] Dairelerin karelerle değiştirildiği ve bir matris biçiminde düzenlendiği Venn diyagramının bir iyileştirmesi . Veitch diyagramı kareler etiketler mintermlerin . Karnaugh , karelere ve etiketlerine 1'ler ve 0'lar atadı ve ortak kullanımdaki numaralandırma şemasını çıkardı.
• Maxfield, Clive "Max" (2006-11-29). "Reed-Müller Mantık" . Mantık 101 . EE Times . Bölüm 3. 2017-04-19 tarihinde kaynağından arşivlendi . 2017-04-19 alındı .
• Lind, Larry Frederick; Nelson, John Christopher Cunliffe (1977). "Bölüm 2.3". Sıralı Sayısal Sistemlerin Analizi ve Tasarımı . Macmillan Basın . ISBN'si 0-33319266-4. (146 sayfa)
• Tutucu, Michel Elizabeth (Mart 2005) [2005-02-14]. "Bir değiştirilmiş Karnaugh harita tekniği" . Eğitimde IEEE İşlemleri . IEEE . 48 (1): 206–207. doi : 10.1109/TE.2004.832879 . eISSN  1557-9638 . ISSN  0018-9359 . S2CID  25576523 . [2]
• Kavanagh, Joseph (2008). Bilgisayar Aritmetiği ve Verilog HDL Temelleri (1 ed.). CRC Basın .
• Kohavi, Zvi; Jha, Niraj K. (2009). Anahtarlama ve Sonlu Otomata Teorisi (3 ed.). Cambridge Üniversitesi Yayınları . ISBN'si 978-0-521-85748-2.

Dış bağlantılar

• Çakışan Dikdörtgenleri Algıla , Herbert Glarner.
• Karnaugh haritalarının pratik uygulamalarda kullanılması , Trafik ışıklarının kontrol edilmesi için Devre tasarımı projesi.
• 2,3,4 ve 5 değişken için K-Map Eğitimi
• Karnaugh Haritası Örneği
• CEP-PC BOOLE FONKSİYONU SADELEŞTİRME, Ledion Bitincka — George E. Antoniou
• K-Map sorun giderme