Kesişim (Öklid geometrisi) - Intersection (Euclidean geometry)

İn geometrisi , bir kesişme (çizgiler, eğriler, düzlem ve yüzey olarak) iki ya da daha çok nesne için bir nokta, çizgi veya eğri yaygındır. Öklid geometrisindeki en basit durum , ya bir nokta olan ya da doğrular paralel ise var olmayan iki farklı doğrunun kesişimidir .

Dairelerin kesişiminin belirlenmesi – daha yüksek boyutlu bir uzaya gömülü doğrusal geometrik nesneler – doğrusal cebirin basit bir görevidir , yani bir doğrusal denklem sisteminin çözümü . Genel olarak bir kesişimin belirlenmesi, örneğin Newton yinelemesi kullanılarak sayısal olarak çözülebilen doğrusal olmayan denklemlere yol açar . Bir doğru ile bir konik bölüm (daire, elips, parabol vb.) veya bir kuadrik (küre, silindir, hiperboloid vb.) arasındaki kesişme problemleri , kolayca çözülebilen ikinci dereceden denklemlere yol açar . Dörtgenler arasındaki kesişmeler , cebirsel olarak çözülebilen dörtlü denklemlere yol açar .

Uçakta

İki çizgi

Paralel olmayan iki doğrunun kesişme noktasının belirlenmesi için

${\displaystyle a_{1}x+b_{1}y=c_{1},\ a_{2}x+b_{2}y=c_{2}}$

itibaren, alır Cramer kuralı veya bir değişken kesişme noktasının koordinatları ile değiştirilmesiyle  : ${\görüntüleme stili (x_{s},y_{s})}$

${\displaystyle x_{s}={\frac {c_{1}b_{2}-c_{2}b_{1}}{a_{1}b_{2}-a_{2}b_{1}}} ,\quad y_{s}={\frac {a_{1}c_{2}-a_{2}c_{1}}{a_{1}b_{2}-a_{2}b_{1}}} .\ }$

(Doğrular paralelse ve bu formüller 0'a bölmeyi içerdiğinden kullanılamaz.) ${\displaystyle a_{1}b_{2}-a_{2}b_{1}=0}$

İki çizgi parçası

Paralel olmayan iki doğru parçası için ve mutlaka bir kesişme noktası yoktur (şemaya bakın), çünkü karşılık gelen doğruların kesişme noktasının doğru bölümlerinde yer alması gerekmez. Durumu kontrol etmek için çizgilerin parametrik gösterimleri kullanılır: ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2})}$${\displaystyle (x_{3},y_{3}),(x_{4},y_{4})}$${\görüntüleme stili (x_{0},y_{0})}$

${\displaystyle (x(s),y(s))=(x_{1}+s(x_{2}-x_{1}),y_{1}+s(y_{2}-y_{1} ))),}$

${\displaystyle (x(t),y(t))=(x_{3}+t(x_{4}-x_{3}),y_{3}+t(y_{4}-y_{3} )))$

Doğru parçaları , ilgili parametreler koşulu yerine getiriyorsa, yalnızca karşılık gelen doğruların ortak noktasında kesişir . Parametreler lineer sistemin çözümüdür ${\görüntüleme stili (x_{0},y_{0})}$${\displaystyle s_{0},t_{0}}$${\displaystyle 0\leq s_{0},t_{0}\leq 1}$${\displaystyle s_{0},t_{0}}$

${\displaystyle s(x_{2}-x_{1})-t(x_{4}-x_{3})=x_{3}-x_{1},}$

${\displaystyle s(y_{2}-y_{1})-t(y_{4}-y_{3})=y_{3}-y_{1}\ .}$

Bunun için çözülebilir s ve t Cramer kuralı kullanarak (bkz yukarıdaki ). Koşul yerine getirilirse, ilgili parametrik gösterime veya eklenir ve kesişme noktası alınır . ${\displaystyle 0\leq s_{0},t_{0}\leq 1}$${\displaystyle s_{0}}$${\görüntüleme stili t_{0}}$${\görüntüleme stili (x_{0},y_{0})}$

Örnek: Doğru parçaları için ve biri doğrusal sistemi alır ${\görüntüleme stili (1,1),(3,2)}$${\görüntüleme stili (1,4),(2,-1)}$

${\ Displaystyle 2s-t=0}$

${\ Displaystyle s+5t=3}$

ve . Bunun anlamı şudur: çizgiler noktada kesişir . ${\displaystyle s_{0}={\tfrac {3}{11}},t_{0}={\tfrac {6}{11}}}$${\displaystyle ({\tfrac {17}{11}},{\tfrac {14}{11}})}$

Not: nokta çiftleri tarafından tayin yerine bölümlerinin göz önüne alındığında hatları, her koşul düşmüş olabilir ve metot hatları (bakınız kesişme noktasını vermektedir yukarıda ). ${\displaystyle 0\leq s_{0},t_{0}\leq 1}$

Bir çizgi ve bir daire

kesişimi için

• çizgi ve daire${\displaystyle balta+by=c}$ ${\displaystyle x^{2}+y^{2}=r^{2}}$

Bir çözer için doğru denklemi x ya da y ve ikame dairenin denklem haline ve (ikinci dereceden denkleminin formül kullanılarak) çözüm alır ile ${\displaystyle (x_{1},y_{1}),(x_{2},y_{2})}$

${\displaystyle x_{1/2}={\frac {ac\pm b{\sqrt {r^{2}(a^{2}+b^{2})-c^{2}}}}{ a^{2}+b^{2}}}\ ,}$

${\displaystyle y_{1/2}={\frac {bc\mp a{\sqrt {r^{2}(a^{2}+b^{2})-c^{2}}}}{ a^{2}+b^{2}}}\ ,}$

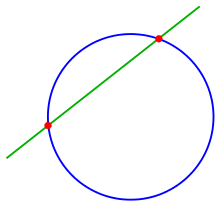
eğer bu koşul katı bir eşitsizlik ile sağlanıyorsa, iki kesişme noktası vardır; bu durumda çizgiye dairenin kesen çizgisi denir ve kesişme noktalarını birleştiren çizgi parçasına dairenin kirişi denir . ${\displaystyle r^{2}(a^{2}+b^{2})-c^{2}\geq 0\ .}$

Eğer tutan, yalnızca bir kesişme noktasını var ve hat daireye teğettir. Zayıf eşitsizlik geçerli değilse, doğru daireyi kesmez. ${\displaystyle r^{2}(a^{2}+b^{2})-c^{2}=0}$

Çemberin orta noktası orijin değilse, bkz. Bir doğrunun ve bir parabolün veya hiperbolün kesişimi benzer şekilde ele alınabilir.

iki daire

İki çemberin kesişme noktalarının belirlenmesi

• ${\displaystyle (x-x_{1})^{2}+(y-y_{1})^{2}=r_{1}^{2},\ \quad (x-x_{2})^ {2}+(y-y_{2})^{2}=r_{2}^{2}}$

bir çizgi ve bir daireyi kesen önceki duruma indirgenebilir. Verilen iki denklemin çıkarılmasıyla doğru denklemi elde edilir:

${\displaystyle 2(x_{2}-x_{1})x+2(y_{2}-y_{1})y=r_{1}^{2}-x_{1}^{2}-y_ {1}^{2}-r_{2}^{2}+x_{2}^{2}+y_{2}^{2}.}$

Bu özel çizgi, iki dairenin radikal çizgisidir .

Özel durum  :${\displaystyle \;x_{1}=y_{1}=y_{2}=0}$
Bu durumda orijin birinci dairenin merkezidir ve ikinci merkez x ekseni (s. diyagramı) üzerindedir. Radikal hattı basitleştirir denklemi ve kesişme noktaları olarak yazılabilir ile ${\displaystyle \;2x_{2}x=r_{1}^{2}-r_{2}^{2}+x_{2}^{2}\;}$${\görüntüleme stili (x_{0},\pm y_{0})}$

${\displaystyle x_{0}={\frac {r_{1}^{2}-r_{2}^{2}+x_{2}^{2}}{2x_{2}}},\quad y_ {0}={\sqrt {r_{1}^{2}-x_{0}^{2}}}\ .}$

Dairelerin ortak noktası olmaması durumunda . Dairelerin ortak bir noktası olması durumunda ve radikal çizgi ortak bir teğettir. ${\displaystyle r_{1}^{2}<x_{0}^{2}}$
${\displaystyle r_{1}^{2}=x_{0}^{2}}$

Yukarıda yazıldığı gibi herhangi bir genel durum, bir kaydırma ve döndürme ile özel duruma dönüştürülebilir.

İki diskin kesişimi (iki dairenin iç kısmı) mercek adı verilen bir şekil oluşturur .

İki konik bölüm

Bir elips/hiperbol/parabolün başka bir konik bölümle kesişimi sorunu, özel durumlarda bir koordinatın ortadan kaldırılmasıyla kolayca çözülebilen ikinci dereceden bir denklem sistemine yol açar . Bir çözüm elde etmek için konik bölümlerin özel özellikleri kullanılabilir . Genel olarak kesişim noktaları, denklem bir Newton iterasyonu ile çözülerek belirlenebilir. Eğer a) her iki konik de örtük olarak verilmişse (bir denklem ile) 2 boyutlu Newton yinelemesi b) biri örtük olarak ve diğeri parametrik olarak 1 boyutlu Newton yinelemesi olarak verilmişse gereklidir. Sonraki bölüme bakın.

İki pürüzsüz eğri

(İki boyutlu uzayda) sürekli türevlenebilen (yani keskin bir bükülme olmayan) iki eğri , düzlemin ortak bir noktasına sahiplerse ve bu noktada sahiplerse bir kesişme noktasına sahiptir. ${\displaystyle \mathbb {R} ^{2}}$

a: farklı teğet çizgiler ( enine kesişim ) veya

b: ortak teğet çizgi ve birbirlerini kesiyorlar ( kesişme noktasına dokunuyor , şemaya bakın).

Her iki eğrinin de bir S noktası ve ortak teğet doğrusu varsa, ancak birbirini kesmiyorsa , sadece S noktasında dokunuyorlar .

Birbirine temas eden kavşaklar nadiren görüldüğü ve ele alınması zor olduğu için, aşağıdaki hususlar bu durumu göz ardı etmektedir. Her durumda, aşağıda gerekli tüm diferansiyel koşullar varsayılır. Kesişme noktalarının belirlenmesi her zaman Newton iterasyonu ile çözülebilen bir veya iki doğrusal olmayan denkleme yol açar. Görünen vakaların listesi aşağıdaki gibidir:

• Her iki eğri de açıkça verilmişse: , onları eşitlemek denklemi verir${\displaystyle y=f_{1}(x),\ y=f_{2}(x)}$

${\displaystyle f_{1}(x)=f_{2}(x)\ .}$

• Her iki eğri de parametrik olarak verilirse:${\displaystyle C_{1}:(x_{1}(t),y_{1}(t)),\ C_{2}:(x_{2}(s),y_{2}(s)). }$

Bunları eşitlemek, iki değişkende iki denklem verir:

${\displaystyle x_{1}(t)=x_{2}(s),\ y_{1}(t)=y_{2}(s)\ .}$

• Eğrilerden biri parametrik, diğeri örtük olarak verilmişse:${\displaystyle C_{1}:(x_{1}(t),y_{1}(t)),\ C_{2}:f(x,y)=0.}$

Bu, açık durumun yanı sıra en basit durumdur. Parametrik gösterimi eğri denklemine eklemek gerekir ve biri denklemi alır: ${\görüntüleme stili C_{1}}$${\görüntüleme stili f(x,y)=0}$${\ Displaystyle C_{2}}$

${\displaystyle f(x_{1}(t),y_{2}(t))=0\ .}$

• Her iki eğri de dolaylı olarak verilirse:${\displaystyle C_{1}:f_{1}(x,y)=0,\ C_{2}:f_{2}(x,y)=0.}$

Burada bir kesişme noktası sistemin bir çözümüdür.

${\displaystyle f_{1}(x,y)=0,\ f_{2}(x,y)=0\ .}$

Herhangi bir Newton yinelemesi, her iki eğrinin de görselleştirilmesiyle elde edilebilecek uygun başlangıç ​​değerlerine ihtiyaç duyar. Parametrik veya açıkça verilen bir eğri kolayca görselleştirilebilir, çünkü sırasıyla herhangi bir t veya x parametresine karşılık gelen noktayı hesaplamak kolaydır. Örtülü olarak verilen eğriler için bu görev o kadar kolay değildir. Bu durumda, başlangıç ​​değerleri ve bir yineleme yardımıyla bir eğri noktası belirlenmelidir. Görmek .

Örnekler:

1: ve daire (şemaya bakın). ${\displaystyle C_{1}:(t,t^{3})}$${\displaystyle C_{2}:(x-1)^{2}+(y-1)^{2}-10=0}$

İşlev için Newton yinelemesi${\displaystyle t_{n+1}:=t_{n}-{\frac {f(t_{n})}{f'(t_{n})}}}$

${\displaystyle f(t)=(t-1)^{2}+(t^{3}-1)^{2}-10}$yapılması gerekiyor. Başlangıç ​​değerleri olarak -1 ve 1.5 seçilebilir.

Kesişme noktaları şunlardır: (−1.1073, −1.3578), (1.6011, 4.1046)

2:${\displaystyle C_{1}:f_{1}(x,y)=x^{4}+y^{4}-1=0,}$

${\displaystyle C_{2}:f_{2}(x,y)=(x-0.5)^{2}+(y-0.5)^{2}-1=0}$ (şemaya bakın).

Newton yinelemesi

${\displaystyle {x_{n+1} \y_ seç{n+1}}={x_{n}+\delta _{x} \y_{n}+\delta _{y}}} seç$yapılması gerekiyor , lineer sistemin çözümü nerede${\displaystyle {\delta _{x} \seçin\delta _{y}}}$

${\displaystyle {\begin{pmatrix}{\frac {\partial f_{1}}{\partial x}}&{\frac {\partial f_{1}}{\partial y}}\\{\frac { \partial f_{2}}{\partial x}}&{\frac {\partial f_{2}}{\partial y}}\end{pmatrix}}{\delta _{x} \choose \delta _{ y}}={-f_{1} \seçin -f_{2}}}$noktada . Başlangıç ​​değerleri olarak (−0.5, 1) ve (1, −0.5) seçilebilir.${\görüntüleme stili (x_{n},y_{n})}$

Lineer sistem Cramer kuralı ile çözülebilir.

Kesişme noktaları (-0,3686, 0,9953) ve (0,9953, -0,3686)'dir.

iki çokgen

Bir ya da iki kesişme noktalarını belirlemek isterse çokgen , bir çokgen (bakınız çizgi bölümlerinin her çiftinin kesişim kontrol edebilir yukarıda ). Çok parçalı çokgenler için bu yöntem oldukça zaman alıcıdır. Pratikte, pencere testleri kullanılarak kesişim algoritması hızlandırılır . Bu durumda, çokgenler küçük alt çokgenlere bölünür ve herhangi bir alt çokgen için en küçük pencere (koordinat eksenlerine paralel kenarları olan dikdörtgen) belirlenir. İki doğru parçasının kesişme noktasının zaman alıcı olarak belirlenmesine başlamadan önce, herhangi bir pencere çifti ortak noktalar için test edilir. Görmek.

Uzayda (üç boyutlu)

3 boyutlu uzayda eğriler ve yüzeyler arasında kesişme noktaları (ortak noktalar) vardır. Aşağıdaki bölümlerde sadece enine kesişimi ele alacağız .

Bir çizgi ve bir uçak

Bir satır ve bir düzlemin kesişimi olarak genel konumda üç boyutta bir noktadır.

Genellikle uzayda bir çizgi parametrik olarak ve bir düzlem bir denklemle temsil edilir . Parametre gösterimini denkleme eklemek, doğrusal denklemi verir ${\görüntüleme stili (x(t),y(t),z(t))}$${\displaystyle balta+by+cz=d}$

${\displaystyle ax(t)+by(t)+cz(t)=d\ ,}$

kesişim noktasının parametresi için . ${\görüntüleme stili t_{0}}$${\görüntüleme stili (x(t_{0}),y(t_{0}),z(t_{0}))}$

Doğrusal denklemin çözümü yoksa, doğru ya düzlem üzerindedir ya da ona paraleldir.

üç uçak

Bir doğru, kesişen iki düzlem tarafından tanımlanıyorsa ve üçüncü bir düzlemle kesişmesi gerekiyorsa, üç düzlemin ortak kesişme noktası değerlendirilmelidir. ${\displaystyle \varepsilon _{i}:\ {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\ i=1,2}$${\displaystyle \varepsilon _{3}:\ {\vec {n}}_{3}\cdot {\vec {x}}=d_{3}}$

Doğrusal bağımsız normal vektörlere sahip üç düzlemin kesişme noktası vardır. ${\displaystyle \varepsilon _{i}:\ {\vec {n}}_{i}\cdot {\vec {x}}=d_{i},\ i=1,2,3}$${\displaystyle {\vec {n}}_{1},{\vec {n}}_{2},{\vec {n}}_{3}}$

${\displaystyle {\vec {p}}_{0}={\frac {d_{1}({\vec {n}}_{2}\times {\vec {n}}_{3}))+ d_{2}({\vec {n}}_{3}\times {\vec {n}}_{1})+d_{3}({\vec {n}}_{1}\times { \vec {n}}_{2})}{{\vec {n}}_{1}\cdot ({\vec {n}}_{2}\times {\vec {n}}_{3 })}}\ .}$

İspat için bir skaler üçlü çarpım kurallarını kullanarak kurulmalıdır . Eğer skaler üçlü çarpım 0'a eşitse, o zaman düzlemlerde ya üçlü kesişim yoktur ya da bu bir doğrudur (ya da üç düzlemin hepsi aynıysa bir düzlemdir). ${\displaystyle {\vec {n}}_{i}\cdot {\vec {p}}_{0}=d_{i},\ i=1,2,3,}$

Bir eğri ve bir yüzey

Düzlem durumuna benzer şekilde, aşağıdaki durumlar 1 veya 3 boyutlu Newton yinelemesi kullanılarak çözülebilen doğrusal olmayan sistemlere yol açar.

• parametrik eğri ve${\görüntüleme stili C:(x(t),y(t),z(t))}$

parametrik yüzey ${\ Displaystyle S:(x(u,v),y(u,v),z(u,v))\ ,}$

• parametrik eğri ve${\görüntüleme stili C:(x(t),y(t),z(t))}$

örtük yüzey ${\displaystyle S:f(x,y,z)=0\ .}$

Örnek:

parametrik eğri ve${\ Displaystyle C:(t,t^{2},t^{3})}$

örtük yüzey (s. resim).${\displaystyle S:x^{4}+y^{4}+z^{4}-1=0}$

Kesişme noktaları şunlardır: (−0.8587, 0.7374, −0.6332), (0.8587, 0.7374, 0.6332).

Bir çizgi-küre kesişimi basit bir özel durumdur.

Bir satır ve bir düzlem halinde olduğu gibi, bir eğri kesişimi ve bir yüzey olarak genel pozisyonda ayrı ayrı noktalar oluşur, ancak bir eğri, kısmen ya da tamamen bir yüzey içinde yer alabilir.

Bir çizgi ve çokyüzlü

iki yüzey

Enine kesişen iki yüzey bir kesişme eğrisi verir . En basit durum, paralel olmayan iki düzlemin kesişme çizgisidir.

Ayrıca bakınız

• hesaplamalı geometri
• bir çizginin denklemi
• Kavşak (küme teorisi)
• kesişim teorisi

Referanslar

daha fazla okuma

• Nicholas M. Patrikalakis ve Takashi Maekawa, Bilgisayar Destekli Tasarım ve İmalat için Şekil Sorgulama , Springer, 2002, ISBN  3540424547 , 9783540424543, s. 408. [1]