Hilbert uzayı - Hilbert space

Gelen matematik , Hilbert uzayları (adını David Hilber ) yöntemlerini genelleme izin doğrusal cebir ve hesabın iki boyutlu ile üç boyutlu gelen Öklid boşluklar sonsuz olabilir boşluklarına boyutu . Hilbert uzayı, bir uzaklık fonksiyonu ve diklik ( bu bağlamda ortogonallik olarak bilinir) tanımlamaya izin veren bir iç çarpım işlemiyle donatılmış bir vektör uzayıdır . Ayrıca, bu mesafe için Hilbert uzayları tamdır , bu da uzayda kalkülüs tekniklerinin kullanılmasına izin verecek yeterli limit olduğu anlamına gelir .

Hilbert uzayları, matematik ve fizikte doğal olarak ve sıklıkla , tipik olarak sonsuz boyutlu fonksiyon uzayları olarak ortaya çıkar . En eski Hilbert uzayları 20. yüzyılın ilk on yılında David Hilbert , Erhard Schmidt ve Frigyes Riesz tarafından bu bakış açısıyla incelenmiştir . Kısmi diferansiyel denklemler , kuantum mekaniği , Fourier analizi ( sinyal işleme ve ısı transferi uygulamalarını içerir ) ve ergodik teori ( termodinamiğin matematiksel temelini oluşturan ) teorilerinde vazgeçilmez araçlardır . John von Neumann , bu çeşitli uygulamaların çoğunun altında yatan soyut kavram için Hilbert uzayı terimini kullandı . Hilbert uzay yöntemlerinin başarısı, işlevsel analiz için çok verimli bir dönemin başlangıcı oldu . Yanı sıra klasik Öklid boşluklarından Hilbert boşlukların örnekleri arasında kare integrallenebilen fonksiyonların boşluk , dizilerin boşluk , sobolev boşluk oluşturduğu genel işlevleri ve Hardy boşluk arasında Holomorfik fonksiyonların .

Geometrik sezgi, Hilbert uzay teorisinin birçok alanında önemli bir rol oynar. Pisagor teoremi ve paralelkenar yasasının tam analogları Hilbert uzayında tutulur. Daha derin bir seviyede, bir alt uzaya dik izdüşüm (bir üçgenin " yüksekliğini düşürmenin " analoğu ), optimizasyon problemlerinde ve teorinin diğer yönlerinde önemli bir rol oynar. Hilbert uzayının bir elemanı , düzlemdeki Kartezyen koordinatlara benzer şekilde, bir dizi koordinat eksenine (bir ortonormal temel ) göre koordinatlarıyla benzersiz bir şekilde belirtilebilir . Bu eksen kümesi sayılabilir sonsuz olduğunda, Hilbert uzayı , kare-toplanabilir sonsuz dizilerin uzayı açısından da yararlı bir şekilde düşünülebilir . İkinci uzay olarak adlandırılan eski literatürde genellikle Hilbert uzay. Hilbert uzayındaki lineer operatörler de aynı şekilde oldukça somut nesnelerdir: iyi durumlarda, uzayı farklı faktörlerle karşılıklı olarak dik yönlerde geren dönüşümlerdir, bir anlamda spektrumlarının incelenmesiyle kesinlik kazanırlar .

Tanım ve illüstrasyon

Motive edici örnek: Öklid vektör uzayı

Hilbert alanı en tanıdık örneklerinden biri Öklid vektör uzayı üç boyutlu oluşan vektörler ile belirtilen R ³ ve donatılmış nokta ürün . Nokta çarpım, x ve y olmak üzere iki vektör alır ve x ⋅ y gerçek sayısını üretir . Eğer x ve y temsil edilmektedir Kartezyen koordinatları , o zaman nokta ürün ile tanımlanır

${\displaystyle {\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\y_{2}\ \y_{3}\end{pmatrix}}=x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}\,.}$

Nokta çarpım şu özellikleri karşılar:

1. Bu simetrik olan x ve y : x ⋅ y = Y ⋅ x .
2. Bu ise , doğrusal olan İlk bileşen olarak: ( a x ₁ + b x ₂ ) ⋅ y = a x ₁ ⋅ y + b x ₂ ⋅ y herhangi skalerler için bir , B , ve vektörler x ₁ , x ₂ , ve y .
3. Bu ise pozitif tanımlı : tüm vektörler için X , X ⋅ x ≥ 0 , eşitlik , ancak ve ancak, eğer x = 0 .

Nokta çarpım gibi bu üç özelliği karşılayan vektör çiftleri üzerinde bir işlem (gerçek) iç çarpım olarak bilinir . Böyle bir iç çarpım ile donatılmış bir vektör uzayı , (gerçek) bir iç çarpım uzayı olarak bilinir . Her sonlu boyutlu iç çarpım uzayı aynı zamanda bir Hilbert uzayıdır. Nokta çarpımını Öklid geometrisine bağlayan temel özelliği, || ile gösterilen bir vektörün hem uzunluğu (veya normu ) ile ilişkili olmasıdır. x || , ve formül aracılığıyla iki x ve y vektörü arasındaki θ açısına

${\displaystyle \mathbf {x} \cdot \mathbf {y} =\sol\|\mathbf {x} \sağ\|\sol\|\mathbf {y} \sağ\|\,\cos \theta \, .}$

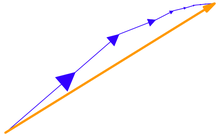
Öklid uzayındaki çok değişkenli hesap , limitleri hesaplama yeteneğine ve limitlerin var olduğu sonucuna varmak için faydalı kriterlere sahip olmasına dayanır . Bir matematiksel serisi

${\displaystyle \sum _{n=0}^{\infty }\mathbf {x} _{n}}$

vektörlerin meydana R ³ olduğu mutlak yakınsak sağlanan gerçek sayılar normal bir dizi uzunlukları yakınsak toplamı:

${\displaystyle \sum _{k=0}^{\infty }\|\mathbf {x} _{k}\|<\infty \,.}$

Bir dizi skalerde olduğu gibi, mutlak yakınsayan bir dizi vektör de Öklid uzayında bir sınır vektörü L'ye yakınsar , şu anlamda

${\displaystyle \left\|\mathbf {L} -\sum _{k=0}^{N}\mathbf {x} _{k}\right\|\to 0\quad {\text{as }} N\to \infty \,.}$

Bu özellik , Öklid uzayının tamlığını ifade eder : Mutlak yakınsayan bir seri aynı zamanda sıradan anlamda da yakınsar.

Hilbert uzayları genellikle karmaşık sayılar üzerinden alınır . Kompleks düzlem ile gösterilen C büyüklükte bir kavramı ile donatılmış olup, kompleks modülü | z | karmaşık eşleniği ile z'nin çarpımının karekökü olarak tanımlanır :

${\displaystyle |z|^{2}=z{\overline {z}}\,.}$

Eğer z = x + iy bir ayrışma olduğunu z ardından modülü normal Öklid iki boyutlu uzunluğu, gerçek ve sanal parçaya olan:

${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}\,.}$

Karmaşık sayılar, bir çift iç çarpımı z ve w ürünüdür z kompleks konjügatı ile ağırlık :

${\displaystyle \langle z,w\rangle =z{\overline {w}}\,.}$

Bu karmaşık değerlidir. ⟨ z , w ⟩'nin gerçek kısmı olağan iki boyutlu Öklid nokta çarpımını verir .

İkinci bir örnek , elemanları z = ( z ₁ , z ₂ ) karmaşık sayı çiftleri olan C ² uzayıdır . Daha sonra z'nin başka bir w = ( w ₁ , w ₂ ) vektörü ile iç çarpımı şu şekilde verilir:

${\displaystyle \langle z,w\rangle =z_{1}{\overline {w_{1}}}+z_{2}{\overline {w_{2}}}\,.}$

⟨ z , w ⟩'nin gerçek kısmı iki boyutlu Öklid nokta çarpımıdır . Bu iç çarpım Hermitian simetriktir, bu da z ve w'nin yer değiştirmesinin sonucunun karmaşık eşlenik olduğu anlamına gelir :

${\displaystyle \langle w,z\rangle ={\overline {\langle z,w\rangle }}\,.}$

Tanım

Bir Hilbert uzayı H a, gerçek veya karmaşık iç çarpım alanı da bir tam metrik alan iç çarpım neden olduğu mesafe fonksiyonuna göre.

Söylemek H a, karmaşık iç çarpım alanı bu araçlar , H , bir iç bir ürün var olan karmaşık bir vektör alanıdır ⟨ x , y ⟩ elemanlarının her çifti için karmaşık bir dizi ilişkilendirerek x , y ve H biri aşağıdaki özellikleri olduğu:

1. İç çarpım eşlenik simetriktir; yani, bir çift elemanın iç çarpımı, değiştirilen elemanların iç çarpımının karmaşık eşleniğine eşittir :

   ${\displaystyle \langle y,x\rangle ={\overline {\langle x,y\rangle }}\,.}$

2. İç çarpım, ilk argümanında doğrusaldır . a ve b tüm karmaşık sayıları için ,

   ${\displaystyle \langle ax_{1}+bx_{2},y\rangle =a\langle x_{1},y\rangle +b\langle x_{2},y\rangle \,.}$

3. Bir elemanın kendisiyle olan iç çarpımı pozitif tanımlıdır :

   ${\displaystyle {\begin{cases}\langle x,x\rangle >0&x\neq 0\\\langle x,x\rangle =0&x=0\,.\end{cases}}}$(Özellik 1'in bunun gerçek olduğunu ima ettiğini unutmayın .)${\görüntüleme stili \langle x,x\rangle }$

Özellikler 1 ve 2'den , ikinci argümanında eşlenik doğrusal olarak da adlandırılan karmaşık bir iç ürünün antilineer olduğu sonucu çıkar .

${\displaystyle \langle x,ay_{1}+by_{2}\rangle ={\bar {a}}\langle x,y_{1}\rangle +{\bar {b}}\langle x,y_{ 2}\rangle \,.}$

Bir , içsel bir ürün alanı dışında, aynı şekilde tanımlanır , H , gerçek vektör alan ve iç Ürün, gerçek değerleri alır. Bu tür bir iç ürün olacaktır iki-doğrusal harita ve ( H , H , ⟨⋅, ⋅⟩) oluşturacak bir ikili sistem .

Norm gerçek değerli bir fonksiyondur

${\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}\,,}$

ve mesafe d iki nokta arasındaki x , y olarak H norm şartları tanımlanır

${\displaystyle d(x,y)=\|xy\|={\sqrt {\langle xy,xy\rangle }}\,.}$

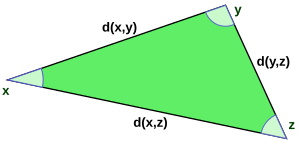
Bu fonksiyonun bir uzaklık fonksiyonu olması, öncelikle x ve y'de simetrik olduğu , ikinci olarak x ile kendisi arasındaki uzaklığın sıfır olduğu, aksi halde x ve y arasındaki uzaklığın pozitif olması gerektiği ve son olarak da üçgen eşitsizliğinin geçerli olduğu anlamına gelir. bir xyz üçgeninin bir ayağının uzunluğu, diğer iki ayağın uzunluklarının toplamını aşamaz:

${\görüntüleme stili d(x,z)\leq d(x,y)+d(y,z)\,.}$

Bu son özellik, sonuçta daha temel bir sonucudur Cauchy- Schwarz eşitsizliği ileri sürerken,

${\displaystyle {\bigl |}\langle x,y\rangle {\bigr |}\leq \sol\|x\sağ\|\sol\|y\sağ\|}$

eşitlikle ancak ve ancak x ve y olan doğrusal bağımlı .

Bu şekilde tanımlanan bir uzaklık fonksiyonu ile, herhangi bir iç çarpım uzayı bir metrik uzaydır ve bazen Hausdorff ön Hilbert uzayı olarak bilinir . Ek olarak tam bir uzay olan herhangi bir Hilbert öncesi uzay bir Hilbert uzayıdır.

Eksiksiz bir H bir formu eksprese edilir Cauchy kriter olarak sekansları için , H , bir ön-Hilbert alanı: H tam olup olmadığını her Cauchy dizisi bu norma göre yakınsak uzayda bir elemana. Tamlık, aşağıdaki eşdeğer koşulla karakterize edilebilir: eğer bir dizi vektör

${\displaystyle \sum _{k=0}^{\infty}u_{k}}$

kesinlikle birleşir şu anlamda

${\displaystyle \sum _{k=0}^{\infty }\|u_{k}\|<\infty \,,}$

o zaman seri , kısmi toplamların H'nin bir öğesine yakınsaması anlamında H'de yakınsar .

Tam bir normlu uzay olarak, Hilbert uzayları tanım gereği aynı zamanda Banach uzaylarıdır . Bu nedenle bunlar topolojik vektör uzayı içinde, topolojik gibi kavramları açıklık ve Kapalılığı alt kümelerini de tanımlandığı gibidir. Kısıtlamanın neden olduğu iç çarpım ile aynı zamanda tam olan (tam bir metrik uzayda kapalı bir küme olmak) ve dolayısıyla kendi başına bir Hilbert uzayı olan bir Hilbert uzayının kapalı lineer alt uzayı kavramı özel bir öneme sahiptir .

İkinci örnek: dizi uzayları

Dizisi alanı l ² tüm oluşur sonsuz diziler Z = ( z ₁ , z ₂ , ...) karmaşık sayılar bu şekilde seri

${\displaystyle \sum _{n=1}^{\infty }|z_{n}|^{2}}$

yakınsar . l ² üzerindeki iç çarpım şu şekilde tanımlanır:

${\displaystyle \langle \mathbf {z} ,\mathbf {w} \rangle =\sum _{n=1}^{\infty}z_{n}{\overline {w_{n}}}\,,}$

Cauchy-Schwarz eşitsizliğinin bir sonucu olarak ikinci seri yakınsamaktadır .

Uzayın tamlığı, l ^2'den gelen bir dizi eleman mutlak olarak (norm olarak) yakınsadığında, o zaman l ^2'nin bir elemanına yakınsaması şartıyla geçerlidir . Kanıt, matematiksel analizde temeldir ve uzayın matematiksel eleman dizilerinin, karmaşık sayılar dizisi (veya sonlu boyutlu Öklid uzayındaki vektörler) ile aynı kolaylıkla manipüle edilmesine izin verir.

Tarih

Hilbert uzaylarının geliştirilmesinden önce, Öklid uzaylarının diğer genellemeleri matematikçiler ve fizikçiler tarafından biliniyordu . Özellikle, soyut bir doğrusal uzay (vektör uzayı) fikri 19. yüzyılın sonlarına doğru bir miktar çekiş kazandı: bu, öğeleri zorunlu olarak bir araya getirilip skalerlerle ( gerçek veya karmaşık sayılar gibi ) çarpılabilen bir uzaydır. bu öğeleri fiziksel sistemlerdeki konum ve momentum vektörleri gibi "geometrik" vektörlerle tanımlama . Özellikle mekanlarda, 20. yüzyılın başında matematikçiler tarafından diğer amaçları dizileri dahil ( dizi ) ve işlevleri boşluklar, doğal olarak doğrusal alanlar olarak düşünülebilir. Örneğin, fonksiyonlar birbirine eklenebilir veya sabit skalerlerle çarpılabilir ve bu işlemler uzamsal vektörlerin toplanması ve skaler çarpımı ile sağlanan cebirsel yasalara uyar.

20. yüzyılın ilk on yılında, paralel gelişmeler Hilbert uzaylarının ortaya çıkmasına neden oldu. Bunlardan ilki, David Hilbert ve Erhard Schmidt'in integral denklemleri çalışması sırasında ortaya çıkan gözlemdi, [ a , b ] aralığında iki kare integrallenebilir reel değerli f ve g fonksiyonunun bir iç çarpımı var.

${\displaystyle \langle f,g\rangle =\int _{a}^{b}f(x)g(x)\,\mathrm {d} x}$

Öklid nokta çarpımının bilinen özelliklerinin çoğuna sahiptir. Özellikle, ortogonal bir fonksiyon ailesi fikrinin bir anlamı vardır. Schmidt , formun bir operatörü için spektral ayrışmanın bir analogunu kanıtlamak için bu iç çarpımın olağan nokta çarpım ile benzerliğinden yararlandı.

${\displaystyle f(x)\mapsto \int _{a}^{b}K(x,y)f(y)\,\mathrm {d} y}$

burada K , x ve y'de simetrik sürekli bir fonksiyondur . Ortaya çıkan özfonksiyon genişletmesi , K fonksiyonunu formun bir dizisi olarak ifade eder .

${\displaystyle K(x,y)=\sum _{n}\lambda _{n}\varphi _{n}(x)\varphi _{n}(y)}$

burada φ _n fonksiyonları , tüm n ≠ m için ⟨ φ _n , φ _m ⟩ = 0 anlamında ortogonaldir . Bu serideki bireysel terimler bazen temel ürün çözümleri olarak adlandırılır. Bununla birlikte, uygun bir anlamda kare-integre edilebilir bir fonksiyona yakınsayamayan özfonksiyon açılımları vardır: yakınsamayı sağlayan eksik bileşen, tamlıktır.

İkinci bir gelişme oldu Lebesgue , alternatif Riemann entegrali ile getirilen Henri Lebesgue mümkün fonksiyonları çok daha geniş bir sınıf entegre yapılmış 1904 Lebesque entegredir. 1907 yılında, Frigyes Riesz ve Ernst Sigismund Fischer , bağımsız bir şekilde boşluk kanıtlamıştır L ² kare Lebesgue integrallenebilen fonksiyonları olan tam metrik alan . Geometri ve tamlık arasındaki etkileşimin bir sonucu olarak, Joseph Fourier , Friedrich Bessel ve Marc-Antoine Parseval'in trigonometrik seriler üzerindeki 19. yüzyıl sonuçları, bu daha genel uzaylara kolayca taşınarak, şimdi genellikle olarak bilinen geometrik ve analitik bir aygıtla sonuçlandı. Riesz-Fischer teoremi .

Daha temel sonuçlar 20. yüzyılın başlarında kanıtlandı. Örneğin, Riesz temsil teoremi , 1907'de Maurice Fréchet ve Frigyes Riesz tarafından bağımsız olarak kuruldu . John von Neumann , sınırsız Hermit operatörleri üzerindeki çalışmasında soyut Hilbert uzayı terimini kullandı . Hermann Weyl ve Norbert Wiener gibi diğer matematikçiler, belirli Hilbert uzaylarını, genellikle fiziksel olarak motive edilmiş bir bakış açısıyla, ayrıntılı olarak zaten incelemiş olsalar da , von Neumann bunların ilk tam ve aksiyomatik tedavisini verdi. Von Neumann daha sonra bunları kuantum mekaniğinin temelleri üzerine çığır açan çalışmasında ve Eugene Wigner ile devam eden çalışmalarında kullandı . "Hilbert uzayı" adı çok geçmeden başkaları tarafından, örneğin Hermann Weyl tarafından kuantum mekaniği ve gruplar teorisi üzerine kitabında benimsendi.

Hilbert uzayı kavramının önemi , kuantum mekaniğinin en iyi matematiksel formülasyonlarından birini sunduğu gerçeğiyle vurgulandı . Kısaca, bir kuantum mekanik sistemin durumları, belirli bir Hilbert uzayında vektörlerdir, gözlenebilirler olan hermisyen operatör bu alan üzerinde, simetrileri sistemi vardır düzgün operatörler ve ölçümler olan ortogonal çıkıntılar . Kuantum mekanik simetri ve üniter operatörler arasındaki ilişki geliştirilmesi için güç vermişti üniter temsil teorisi ait grupların Hermann Weyl 1928 çalışmalarında başlattığı. Öte yandan, 1930'ların başlarında, klasik mekaniğin Hilbert uzayı ( Koopman-von Neumann klasik mekaniği ) terimleriyle tanımlanabileceği ve klasik dinamik sistemlerin belirli özelliklerinin Hilbert uzay teknikleri kullanılarak aşağıdakiler çerçevesinde analiz edilebileceği anlaşıldı. ergodik teori .

Cebri gözlenebilirler kuantum mekaniği göre, doğal olarak, bir Hilbert uzayında tanımlanan operatörleri bir cebir , Werner Heisenberg 'in matris mekaniği kuantum formülasyonu. Von Neumann , 1930'larda bir Hilbert uzayındaki operatör halkaları olarak operatör cebirlerini araştırmaya başladı . Von Neumann ve çağdaşları tarafından incelenen cebir türleri artık von Neumann cebirleri olarak biliniyor . 1940'larda, Israel Gelfand , Mark Naimark ve Irving Segal , C*-cebirleri adı verilen ve bir yandan altta yatan bir Hilbert uzayına hiç gönderme yapmayan ve diğer yandan kullanışlı özelliklerin çoğunu tahmin eden bir tür operatör cebir tanımı yaptılar. Daha önce çalışılmış olan operatör cebirlerinin Özellikle mevcut Hilbert uzay teorisinin çoğunun altında yatan kendine-eşlenik operatörler için spektral teorem, C*-cebirlerine genelleştirildi. Bu teknikler artık soyut harmonik analiz ve temsil teorisinde temeldir.

Örnekler

Lebesgue boşlukları

Lebesgue alanlardır işlev alanları ile ilişkili boşluk ölçülmesi ( X , K , μ ) burada, X, bir dizi, M a, σ cebir ait alt kümelerin X ve μ a, sayılabilir ilave önlem ile M . Let L ² ( X , μ ) üzerinde bu kompleks değerli ölçülebilir fonksiyonların uzay X olan Lebesgue karesinin mutlak değerinin bir fonksiyonu yani fonksiyonunun sonlu, f içinde L ² ( X , μ ) ,

${\displaystyle \int _{X}|f|^{2}\mathrm {d} \mu <\infty \,,}$

ve işlevlerin yalnızca ve yalnızca bir sıfır ölçü kümesinde farklılık göstermeleri durumunda tanımlandığı yer .

İşlevleri olan iç çarpımı f ve g olarak L ² ( X , μ ) aşağıdaki gibi tanımlanır

${\displaystyle \langle f,g\rangle =\int _{X}f(t){\overline {g(t)}}\,\mathrm {d} \mu (t)\ }$ veya ${\displaystyle \ \int _{X}{\overline {f(t)}}g(t)\,\mathrm {d} \mu (t)\,,}$

ikinci formun (birinci elementin konjugasyonu) teorik fizik literatüründe yaygın olarak bulunduğu yer. İçin f ve g olarak L ² , yekpare için Cauchy-Schwartz eşitsizliği bulunur ve alan bir iç ürünü tanımlar. Bu iç ürünle donatılan L ² aslında tamamlandı. Lebesgue integrali, tamlığı sağlamak için gereklidir: örneğin, gerçek sayıların etki alanlarında, Riemann integrali alınabilir işlevler yeterli değildir .

Lebesgue boşlukları birçok doğal ortamda görünür. Alanlarda L ² ( R ) ve L ² ([0,1]) ile ilgili olarak kare integrallenebilen fonksiyonların Lebesgue ölçümü gerçek hattı ve birim aralığında, sırasıyla, Fourier dönüşümü ve Fourier tanımlamak için doğal alanlardır dizi. Diğer durumlarda, ölçü, gerçek çizgideki sıradan Lebesgue ölçüsünden farklı bir şey olabilir. Örneğin, eğer ağırlık pozitif ölçülebilir fonksiyon, tüm ölçülebilir fonksiyonların alanıdır f aralığında [0, 1] tatmin

${\displaystyle \int _{0}^{1}{\bigl |}f(t){\bigr |}^{2}w(t)\,\mathrm {d} t<\infty }$

ağırlıklı L ² uzayı L denir²
_ağırlık([0, 1]) , ve w ağırlık fonksiyonu olarak adlandırılır. İç çarpım şu şekilde tanımlanır:

${\displaystyle \langle f,g\rangle =\int _{0}^{1}f(t){\overline {g(t)}}w(t)\,\mathrm {d} t\,. }$

ağırlıklı uzay L²
_ağırlık([0, 1]) Hilbert uzayı L ² ([0, 1], μ ) ile aynıdır , burada Lebesgue ile ölçülebilir bir A kümesinin μ ölçüsü şu şekilde tanımlanır:

${\displaystyle \mu (A)=\int _{A}w(t)\,\mathrm {d} t\,.}$

Ağırlıklı L ² ortogonal polinomların farklı aileler farklı ağırlık işlevleri açısından dik olduğu için böyle boşlukları sıklıkla, ortogonal polinomları incelemek için kullanılır.

Sobolev uzayları

H ^s veya W ^{s , 2} ile gösterilen Sobolev uzayları Hilbert uzaylarıdır. Bu özel bir tür olan fonksiyon alanı olan farklılaşma gerçekleştirilebilir, ancak bu (diğer farklı Banach boşluklar gibi holder boşluklar ), bir iç ürününün yapısını destekler. Farklılaşmaya izin verildiğinden, Sobolev uzayları kısmi diferansiyel denklemler teorisi için uygun bir ayardır . Ayrıca , varyasyon hesabında doğrudan yöntemler teorisinin temelini oluştururlar .

İçin s , negatif olmayan bir tamsayı ve Ω ⊂ R ^{, n} , sobolev alan lH ^s (Ω) içeren L ² olan fonksiyonları zayıf türevleri için yukarı için s da L ² . H ^s (Ω) cinsinden iç çarpım

${\displaystyle \langle f,g\rangle =\int _{\Omega }f(x){\bar {g}}(x)\,\mathrm {d} x+\int _{\Omega }Df(x) )\cdot D{\bar {g}}(x)\,\mathrm {d} x+\cdots +\int _{\Omega }D^{s}f(x)\cdot D^{s}{\ çubuk {g}}(x)\,\mathrm {d} x}$

burada nokta, her mertebenin kısmi türevlerinin Öklid uzayındaki nokta çarpımını gösterir. Sobolev uzayları, s bir tamsayı olmadığında da tanımlanabilir .

Sobolev uzayları, daha spesifik olarak Hilbert uzay yapısına dayanarak, spektral teori açısından da incelenir. Eğer Ω uygun bir bölge ise, o zaman Sobolev uzayı H ^s (Ω) Bessel potansiyellerinin uzayı olarak tanımlanabilir ; kabaca,

${\displaystyle H^{s}(\Omega )=\left.\left\{(1-\Delta )^{-{\frac {s}{2}}}f\;\sağ|\,f\ L^{2}(\Omega )\right\}\,.} içinde$

Burada Δ Laplacian'dır ve (1 − Δ) ^{− s/2}spektral haritalama teoremi açısından anlaşılır . Tamsayı olmayan s için Sobolev uzaylarının uygulanabilir bir tanımını sağlamanın yanı sıra , bu tanım aynı zamanda Fourier dönüşümü altında onu sözde diferansiyel operatörlerin incelenmesi için ideal kılan özellikle arzu edilen özelliklere sahiptir . Bu yöntemleri bir kompakt Riemann manifoldu üzerinde kullanarak , örneğin Hodge teorisinin temeli olan Hodge ayrıştırması elde edilebilir .

Holomorfik fonksiyonların uzayları

dayanıklı boşluklar

Hardy alanlarda ortaya çıkan, fonksiyon alanlarda olan kompleks analiz ve harmonik analiz , öğeleri kesin, holomorfik fonksiyonlar karmaşık etki. Let u ifade birimi disk kompleks düzlemde. Daha sonra Hardy alan H ² ( u ) Holomorfik fonksiyonların alan olarak tanımlanmıştır f ilgili U , örneğin araçlarının

${\displaystyle M_{r}(f)={\frac {1}{2\pi }}\int _{0}^{2\pi }\left|f\left(re^{i\theta }\ sağ)\sağ|^{2}\,\mathrm {d} \theta }$

r < 1 için sınırlı kalır . Bu Hardy uzayındaki norm şu şekilde tanımlanır:

${\displaystyle \left\|f\sağ\|_{2}=\lim _{r\to 1}{\sqrt {M_{r}(f)}}\,.}$

Diskteki hardy boşlukları Fourier serisi ile ilgilidir. Bir fonksiyon f olan , H ² ( U ) , ancak ve ancak

${\displaystyle f(z)=\sum _{n=0}^{\infty }a_{n}z^{n}}$

nerede

${\displaystyle \sum _{n=0}^{\infty }|a_{n}|^{2}<\infty \,.}$

Böylece H ² ( U ) , daire üzerinde L ² olan ve negatif frekans Fourier katsayıları yok olan fonksiyonlardan oluşur .

Bergman uzayları

Bergman alanlarda Holomorfik fonksiyonların Hilbert alanlarda başka aileyiz. Let D bir sınırlanan açık bir resim grubu olabilir , kompleks düzlemin (ya da daha yüksek boyutlu kompleks alan) ve izin L ^{2, H} ( D ) Holomorfik fonksiyonların uzay f de D olarak da L ² ( D ) anlamında o

${\displaystyle \|f\|^{2}=\int _{D}|f(z)|^{2}\,\mathrm {d} \mu (z)<\infty \,,}$

burada integral D' deki Lebesgue ölçüsüne göre alınır . Açıkça L ^{2, H} ( D ) arasında bir alt uzay olan L ² ( D ) ; aslında, kapalı bir altuzaydır ve dolayısıyla kendi başına bir Hilbert uzayıdır. Bu geçerli tahminin sonucudur; kompakt alt kümeleri K arasında D o,

${\displaystyle \sup _{z\in K}\left|f(z)\right|\leq C_{K}\left\|f\right\|_{2}\,,}$

bu da Cauchy'nin integral formülünden çıkar . İçinde Holomorfik fonksiyonların bir dizi Böylece yakınsama L ² ( D ) , aynı zamanda da anlaşılacağı kompakt yakınsama ve sınırı fonksiyonu bu yüzden de holomorfik olup. Bu eşitsizliğin bir başka sonucu, bir f fonksiyonunu D noktasında değerlendiren lineer fonksiyonelin aslında L ^{2, h} ( D ) üzerinde sürekli olmasıdır . Riesz temsil teoremi, değerlendirme fonksiyonelinin L ^{2, h} ( D ) ' nin bir elemanı olarak temsil edilebileceğini ima eder . Böylece, her z ∈ D için bir η _z ∈ L ^{2, h} ( D ) fonksiyonu vardır.

${\displaystyle f(z)=\int _{D}f(\zeta ){\overline {\eta _{z}(\zeta )}}\,\mathrm {d} \mu (\zeta )}$

tümü için f ∈ L ^{2, h} ( D ) . integral

${\displaystyle K(\zeta ,z)={\overline {\eta _{z}(\zeta )}}}$

olarak bilinir Bergman çekirdek bölgesinin D . Bu integral çekirdek, bir çoğaltma özelliğini karşılar.

${\displaystyle f(z)=\int _{D}f(\zeta )K(\zeta ,z)\,\mathrm {d} \mu (\zeta )\,.}$

Bir Bergman uzayı, buna benzer bir yeniden üretme özelliğini doğrulayan bir çekirdek K ( ζ , z ) ile birlikte fonksiyonların bir Hilbert uzayı olan yeniden üreten çekirdek Hilbert uzayına bir örnektir . Hardy uzayı H ² ( D ) ayrıca Szegő çekirdeği olarak bilinen çoğalan bir çekirdeği kabul eder . Çekirdeklerin çoğaltılması, matematiğin diğer alanlarında da yaygındır. Örneğin, içinde harmonik analiz Poisson çekirdeği karesi integrallenebilir Hilbert uzayında bir doğuran çekirdek olduğu harmonik fonksiyonlar içinde birim topu . İkincisinin bir Hilbert uzayı olması, harmonik fonksiyonlar için ortalama değer teoreminin bir sonucudur.

Uygulamalar

Hilbert uzaylarının uygulamalarının çoğu, Hilbert uzaylarının, izdüşüm ve temel değişimi gibi basit geometrik kavramların genelleştirmelerini olağan sonlu boyutlu ayarlarından desteklediği gerçeğinden yararlanır . Özellikle, bir Hilbert uzayı üzerindeki sürekli kendine eş doğrusal operatörlerin spektral teorisi , bir matrisin olağan spektral ayrışmasını genelleştirir ve bu, teorinin matematik ve fiziğin diğer alanlarına uygulamalarında sıklıkla önemli bir rol oynar.

Sturm-Liouville teorisi

Adi diferansiyel denklemler teorisinde, uygun bir Hilbert uzayında spektral yöntemler, diferansiyel denklemlerin özdeğerlerinin ve özfonksiyonlarının davranışını incelemek için kullanılır. Örneğin, Sturm-Liouville problemi bir keman teli veya davulundaki dalgaların harmoniklerinin incelenmesinde ortaya çıkar ve adi diferansiyel denklemlerde merkezi bir problemdir . Sorun, formun diferansiyel denklemidir.

${\displaystyle -{\frac {\mathrm {d} }{\mathrm {d} x}}\left[p(x){\frac {\mathrm {d} y}{\mathrm {d} x}} \sağ]+q(x)y=\lambda w(x)y}$

[ a , b ] aralığında bilinmeyen bir y fonksiyonu için , genel homojen Robin sınır koşullarını sağlayan

${\displaystyle {\begin{cases}\alpha y(a)+\alpha 'y'(a)&=0\\\beta y(b)+\beta 'y'(b)&=0\,. \end{durumlar}}}$

p , q ve w fonksiyonları önceden verilmiştir ve problem, denklemin çözümü olan y fonksiyonunu ve λ sabitlerini bulmaktır . Problemin yalnızca sistemin özdeğerleri olarak adlandırılan belirli λ değerleri için çözümleri vardır ve bu, sistem için Green fonksiyonu tarafından tanımlanan integral operatöre uygulanan kompakt operatörler için spektral teoremin bir sonucudur . Ayrıca, bu genel sonucun bir başka sonucu da , sistemin λ öz değerlerinin sonsuza doğru artan bir sırayla düzenlenebilmesidir.

Kısmi diferansiyel denklemler

Hilbert uzayları, kısmi diferansiyel denklemlerin incelenmesinde temel bir araç oluşturur . Lineer eliptik denklemler gibi birçok kısmi diferansiyel denklem sınıfı için, fonksiyon sınıfını genişleterek genelleştirilmiş bir çözümü ( zayıf çözüm olarak bilinir) düşünmek mümkündür . Birçok zayıf formülasyon , bir Hilbert uzayı olan Sobolev fonksiyonlarının sınıfını içerir . Uygun bir zayıf formülasyon, bir çözüm bulma analitik problemini veya daha da önemlisi, bir çözümün var olduğunu ve verilen sınır verileri için benzersiz olduğunu gösteren analitik problemi geometrik bir probleme indirger. Doğrusal eliptik denklemler için, geniş bir problem sınıfı için benzersiz çözülebilirlik sağlayan bir geometrik sonuç Lax-Milgram teoremidir . Bu strateji , kısmi diferansiyel denklemlerin sayısal çözümü için Galerkin yönteminin ( sonlu elemanlar yöntemi ) temelini oluşturur.

Tipik bir örnek , Poisson denklemi -Δ u = gr ile Dirichlet sınır koşulları sınırlı bir alan içinde Q olarak R ² . Zayıf formülasyon, sürekli türevlenebilir tüm v fonksiyonları için Ω in Ω sınırda kaybolacak şekilde bir u fonksiyonu bulmaktan ibarettir :

${\displaystyle \int _{\Omega }\nabla u\cdot \nabla v=\int _{\Omega }gv\,.}$

Bu, Hilbert uzayı H cinsinden yeniden biçimlendirilebilir.¹
₀(Ω) u fonksiyonlarından oluşan, öyle ki u , zayıf kısmi türevleri ile birlikte Ω üzerinde kare integrallenebilir ve sınırda yok olur. O zaman soru bulma azaltır u herkes için bu alanda öyle ki v bu alanda

${\görüntüleme stili a(u,v)=b(v)}$

burada a sürekli bir çift doğrusal biçimdir ve b , sırasıyla verilen sürekli doğrusal bir işlevseldir .

${\displaystyle a(u,v)=\int _{\Omega }\nabla u\cdot \nabla v,\quad b(v)=\int _{\Omega }gv\,.}$

Poisson denklemi olduğundan eliptik , bu çiftdoğrusal formu olduğunu Poincaré'in eşitsizliğinden gelmektedir bir olduğunu zorlayıcı . Lax-Milgram teoremi daha sonra bu denklemin çözümlerinin varlığını ve benzersizliğini sağlar.

Hilbert uzayları birçok eliptik kısmi diferansiyel denklemin benzer şekilde formüle edilmesine izin verir ve bu durumda Lax-Milgram teoremi onların analizinde temel bir araçtır. Uygun modifikasyonlarla, benzer teknikler parabolik kısmi diferansiyel denklemlere ve bazı hiperbolik kısmi diferansiyel denklemlere uygulanabilir .

ergodik teori

Ergodik teori alanı, kaotik dinamik sistemlerin uzun vadeli davranışlarının incelenmesidir . Ergodik teorinin geçerli olduğu bir alanın protipik durumu, bir sistemin mikroskobik durumu son derece karmaşık olmasına rağmen (madde parçacıkları arasındaki bireysel çarpışmalar topluluğunu anlamak imkansızdır) - yeterince uzun bir süre boyunca ortalama davranışın olduğu termodinamiktir. zaman aralıkları izlenebilir. Termodinamik kanunları böyle ortalama davranış hakkında iddialar vardır. Özellikle, termodinamiğin sıfırıncı yasasının bir formülasyonu, yeterince uzun zaman çizelgelerinde, dengedeki bir termodinamik sistemin işlevsel olarak bağımsız tek ölçümünün, sıcaklık biçimindeki toplam enerjisi olduğunu ileri sürer .

Ergodik dinamik sistem, Hamiltonian tarafından ölçülen enerjiden başka , faz uzayında fonksiyonel olarak bağımsız korunan başka niceliğin olmadığı sistemdir . Daha açık bir şekilde, E enerjisinin sabit olduğunu varsayalım ve Ω _E , tüm E enerji durumlarından (bir enerji yüzeyi) oluşan faz uzayının alt kümesi olsun ve T _t , faz uzayındaki evrim operatörünü göstersin. Ω _E üzerinde sabit olmayan sürekli fonksiyonlar yoksa dinamik sistem ergodiktir .

${\görüntüleme stili f(T_{t}w)=f(w)}$

Ω _E üzerindeki tüm w ve tüm t zamanları için . Liouville teoremi , enerji yüzeyinde zaman ötelemesi altında değişmez olan bir μ ölçüsünün var olduğunu ima eder . Bunun bir sonucu olarak, zaman için bir bir üniter dönüşüm Hilbert boşluk, L ² (Ω _E , μ ) enerji yüzeyi üzerinde kare İntegrallenebilir fonksiyonlar oluşan Ω _e iç ürüne göre

${\displaystyle \left\langle f,g\right\rangle _{L^{2}\left(\Omega _{E},\mu \sağ)}=\int _{E}f{\bar {g }}\,\mathrm {d} \mu \,.}$

Von Neumann ortalama ergodik teoremi aşağıdakileri belirtir:

• Eğer U _t Hilbert alanı üzerinde, yekpare bir operatör (kuvvetli sürekli) bir parametreli yarıgrupdur H ve p ortak sabit nokta alanı üzerine dikey çıkıntıdır u _t , { x ∈ H | U _t x = x , ∀ t > 0} , sonra

  ${\displaystyle Px=\lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}U_{t}x\,\mathrm {d} t\, .}$

Ergodik bir sistem için, zaman evriminin sabit kümesi yalnızca sabit fonksiyonlardan oluşur, bu nedenle ergodik teorem aşağıdakileri ima eder: herhangi bir fonksiyon için f ∈ L ² (Ω _E , μ ) ,

${\displaystyle {\underset {T\to \infty }{L^{2}-\lim }}{\frac {1}{T}}\int _{0}^{T}f(T_{t} w)\,\mathrm {d} t=\int _{\Omega _{E}}f(y)\,\mathrm {d} \mu (y)\,.}$

Yani, gözlemlenebilir bir f'nin uzun zaman ortalaması, bir enerji yüzeyi üzerindeki beklenti değerine eşittir.

Fourier analizi

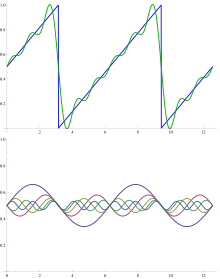
Fourier analizinin temel amaçlarından biri, bir fonksiyonu , verilen temel fonksiyonların (muhtemelen sonsuz) doğrusal bir kombinasyonuna ayrıştırmaktır : ilişkili Fourier serileri . [0, 1] aralığında tanımlanan bir f fonksiyonu ile ilişkili klasik Fourier serisi , şu şekilde bir seridir:

${\displaystyle \sum _{n=-\infty }^{\infty}a_{n}e^{2\pi in\theta}}$

nerede

${\displaystyle a_{n}=\int _{0}^{1}f(\theta )e^{-2\pi in\theta }\,\mathrm {d} \theta \,.}$

Bir testere dişi işlevi için bir Fourier serisindeki ilk birkaç terimi toplama örneği şekilde gösterilmiştir. Temel fonksiyonlar, dalga boylarına sahip sinüs dalgalarıdır.λ/n(tam sayı için n ) dalga boyu daha kısa N- (haricinde testere dişi kendisinin , n = 1 , temel dalga). Tüm temel işlevlerin testere dişinin düğümlerinde düğümleri vardır, ancak temel işlevler hariç tümünde ek düğümler vardır. Testere dişi hakkında toplanan terimlerin salınımına Gibbs fenomeni denir .

Klasik Fourier serilerindeki önemli bir problem, Fourier serisinin hangi anlamda f fonksiyonuna yakınsadığını sorar . Hilbert uzay yöntemleri bu soruya olası bir cevap sağlar. e _n ( θ ) = e ^{2π inθ} fonksiyonları Hilbert uzayı L ² ([0, 1])'in ortogonal bir tabanını oluşturur . Sonuç olarak, herhangi bir kare ile integrallenebilen fonksiyon bir seri olarak ifade edilebilir.

${\displaystyle f(\theta )=\sum _{n}a_{n}e_{n}(\theta )\,,\quad a_{n}=\langle f,e_{n}\rangle }$

ve dahası, bu seri Hilbert uzay anlamında (yani L ² ortalamasında ) yakınsar .

Problem soyut bir bakış açısından da incelenebilir: Her Hilbert uzayının bir ortonormal tabanı vardır ve Hilbert uzayının her elemanı, bu temel elemanların katlarının toplamı olarak benzersiz bir şekilde yazılabilir. Bu temel elemanlar üzerinde görünen katsayılar bazen soyut olarak uzayın elemanının Fourier katsayıları olarak bilinir. Soyutlama, özellikle L ² ([0, 1]) gibi bir uzay için farklı temel fonksiyonların kullanılması daha doğal olduğunda kullanışlıdır . Birçok durumda, bir fonksiyonu trigonometrik fonksiyonlara değil , örneğin ortogonal polinomlara veya dalgacıklara ve daha yüksek boyutlarda küresel harmoniklere ayrıştırmak arzu edilir .

Örneğin, e _n , L ² [0, 1]' nin herhangi bir ortonormal temel işleviyse , o zaman L ² [0, 1]' deki belirli bir işlev, sonlu bir doğrusal kombinasyon olarak tahmin edilebilir.

${\displaystyle f(x)\yaklaşık f_{n}(x)=a_{1}e_{1}(x)+a_{2}e_{2}(x)+\cdots +a_{n}e_{ n}(x)\,.}$

Farkın büyüklüğünü yapmak için { a _j } katsayıları seçilir || f - f _n || ² mümkün olduğunca küçük. Geometrik olarak, en iyi yaklaşım bir dik izdüşüm ve f tüm lineer kombinasyonlarından oluşan matrisini { e _j } ve hesaplanabilir

${\displaystyle a_{j}=\int _{0}^{1}{\overline {e_{j}(x)}}f(x)\,\mathrm {d} x\,.}$

Bu formülün farkı en aza indirdiğini || f - f _n || ² , Bessel eşitsizliğinin ve Parseval formülünün bir sonucudur .

Fiziksel problemlere yönelik çeşitli uygulamalarda, bir fonksiyon bir diferansiyel operatörün (tipik olarak Laplace operatörü ) fiziksel olarak anlamlı özfonksiyonlarına ayrıştırılabilir : bu , diferansiyel operatörün spektrumuna referansla fonksiyonların spektral çalışmasının temelini oluşturur . Somut bir fiziksel uygulama, bir tamburun şeklini duyma problemini içerir : bir davul kafasının üretebildiği temel titreşim modları göz önüne alındığında, tamburun kendisinin şekli çıkarılabilir mi? Bu sorunun matematiksel formülasyonu , keman telinin temel titreşim modlarını temsil eden tamsayılarla doğrudan analoji içinde temel titreşim modlarını temsil eden düzlemdeki Laplace denkleminin Dirichlet özdeğerlerini içerir .

Spektral teori , bir fonksiyonun Fourier dönüşümünün belirli yönlerinin de temelini oluşturur . Fourier analizi, kompakt bir kümede tanımlanan bir fonksiyonu Laplacian'ın (bir keman teli veya davulunun titreşimlerine karşılık gelen) ayrık spektrumuna ayrıştırırken, bir fonksiyonun Fourier dönüşümü, tüm Öklid uzayında tanımlanan bir fonksiyonun ayrıştırılmasıdır. Laplacian'ın sürekli spektrumundaki bileşenlerine . Fourier dönüşümü aynı zamanda , bir Hilbert uzayının ("zaman alanı") diğeriyle ("frekans alanı") bir izometrisi olduğunu iddia eden Plancherel teoremi tarafından kesin kılınan bir anlamda geometriktir . Fourier dönüşümünün bu izometri özelliği, örneğin değişmeli olmayan harmonik analizde meydana gelen küresel fonksiyonlar için Plancherel teoremi tarafından kanıtlandığı gibi (sürekli Fourier Dönüşümü için enerjinin korunumunu yansıttığı için ) soyut harmonik analizde tekrar eden bir temadır .

Kuantum mekaniği

John von Neumann tarafından geliştirilen kuantum mekaniğinin matematiksel olarak titiz formülasyonunda, bir kuantum mekanik sisteminin olası durumları (daha doğrusu saf durumlar ) , bilinen karmaşık bir ayrılabilir Hilbert uzayında bulunan birim vektörler ( durum vektörleri olarak adlandırılır ) ile temsil edilir. olarak durumu alanı , normalin 1 bir karmaşık sayının (kadar tanımlanan faz faktörü ). Başka bir deyişle, olası durumlar , genellikle karmaşık yansıtmalı uzay olarak adlandırılan bir Hilbert uzayının yansıtmasındaki noktalardır . Bu Hilbert uzayının tam doğası sisteme bağlıdır; örneğin, tek bir göreli olmayan spin sıfır parçacığı için konum ve momentum durumları, tüm kare ile integrallenebilen fonksiyonların uzayı iken, tek bir protonun spini için durumlar, iki boyutlu karmaşık Hilbert spinor uzayının birim elemanlarıdır. . Her gözlenebilir, durum uzayı üzerinde hareket eden kendine eş doğrusal bir operatör tarafından temsil edilir . Bir gözlenebilirin her bir özdurumu , operatörün bir özvektörüne karşılık gelir ve ilgili özdeğer , o özdurumdaki gözlenebilirin değerine karşılık gelir.

İki durum vektörü arasındaki iç çarpım, olasılık genliği olarak bilinen karmaşık bir sayıdır . Kuantum mekanik bir sistemin ideal ölçümü sırasında, bir sistemin belirli bir başlangıç ​​durumundan belirli bir öz duruma çökme olasılığı, ilk ve son durumlar arasındaki olasılık genliklerinin mutlak değerinin karesi ile verilir . Bir ölçümün olası sonuçları, operatörün özdeğerleridir; bu, tüm özdeğerlerin gerçek olması gerektiğinden, kendine eş operatörlerin seçimini açıklar. Belirli bir durumda gözlenebilirin olasılık dağılımı, ilgili operatörün spektral ayrışmasının hesaplanmasıyla bulunabilir.

Genel bir sistem için, durumlar tipik olarak saf değildir, bunun yerine yoğunluk matrisleri tarafından verilen saf durumların istatistiksel karışımları veya karışık durumlar olarak temsil edilir : Hilbert uzayı üzerinde iz 1'in kendine-bağlı operatörleri . Ayrıca, genel kuantum mekanik sistemler için, tek bir ölçümün etkileri, bir sistemin diğer parçalarını, bunun yerine pozitif operatör değerli bir ölçü ile tanımlanan şekilde etkileyebilir . Bu nedenle, genel teorideki hem durumların hem de gözlemlenebilirlerin yapısı, saf durumlar için idealleştirmeden çok daha karmaşıktır.

Renk algısı

Herhangi bir gerçek fiziksel renk, saf spektral renklerin bir kombinasyonu ile temsil edilebilir . Fiziksel renkler herhangi bir sayıda spektral renkten oluşabileceğinden, fiziksel renklerin uzayı, spektral renkler üzerinde uygun bir şekilde Hilbert uzayı ile temsil edilebilir. İnsanların renk algısı için üç tip koni hücresi vardır , bu nedenle algılanabilir renkler 3 boyutlu Öklid uzayı ile temsil edilebilir. Hilbert fiziksel renk uzayından, insan tarafından algılanabilen renklerin Öklid uzayına kadar çok-bir doğrusal eşleme, birçok farklı fiziksel rengin insanlar tarafından neden aynı olarak algılanabileceğini açıklar (örneğin, kırmızı ve yeşilin karışımına karşı saf sarı ışık). ışık, bkz. metamerizm ).

Özellikler

Pisagor kimliği

Bir Hilbert uzayında H iki vektörü u ve v , ⟨ u , v ⟩ = 0 olduğunda ortogonaldir . Bunun gösterimi u ⊥ v şeklindedir . Daha genel olarak, ne zaman S bir alt kümesi , H , gösterim u ⊥ S olduğu anlamına gelir u her elemanına dik olan S .

Ne zaman u ve v diktir, birine sahiptir

${\displaystyle \|u+v\|^{2}=\langle u+v,u+v\rangle =\langle u,u\rangle +2\,\operatorname {Re} \langle u,v\rangle +\langle v,v\rangle =\|u\|^{2}+\|v\|^{2}\,.}$

Üzerine tümevarım n , bu herhangi bir aileye uzatılır u ₁ , ..., u _n ait n ortogonal vektörler,

${\displaystyle \left\|u_{1}+\cdots +u_{n}\right\|^{2}=\left\|u_{1}\right\|^{2}+\cdots +\left \|u_{n}\sağ\|^{2}.}$

Belirtildiği gibi Pisagor özdeşliği herhangi bir iç çarpım uzayında geçerliyken, Pisagor kimliğinin seriye genişletilmesi için tamlık gereklidir. Bir dizi Σ u _k bir ortogonal vektörler yakınsak H ancak ve ancak normlar yakınsak karelerinin serisi ve

${\displaystyle \left\|\sum _{k=0}^{\infty }u_{k}\right\|^{2}=\sum _{k=0}^{\infty }\left\| u_{k}\sağ\|^{2}\,.}$

Ayrıca, bir dizi ortogonal vektörün toplamı, alındığı sırada bağımsızdır.

Paralelkenar özdeşliği ve polarizasyon

Tanım olarak, her Hilbert uzayı aynı zamanda bir Banach uzayıdır . Ayrıca, her Hilbert uzayında aşağıdaki paralelkenar özdeşliği bulunur :

${\displaystyle \left\|u+v\sağ\|^{2}+\left\|uv\right\|^{2}=2\left(\left\|u\sağ\|^{2} +\sol\|v\sağ\|^{2}\sağ)\,.}$

Tersine, paralelkenar özdeşliğinin tuttuğu her Banach uzayı bir Hilbert uzayıdır ve iç çarpım, polarizasyon özdeşliği tarafından norm tarafından benzersiz bir şekilde belirlenir . Gerçek Hilbert uzayları için polarizasyon özdeşliği

${\displaystyle \langle u,v\rangle ={\frac {1}{4}}\left(\left\|u+v\right\|^{2}-\left\|uv\right\|^ {2}\sağ)\,.}$

Karmaşık Hilbert uzayları için,

${\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}\left(\left\|u+v\right\|^{2}-\left\|uv\right\|^ {2}+i\left\|u+iv\sağ\|^{2}-i\left\|u-iv\sağ\|^{2}\sağ)\,.}$

Paralelkenar yasası, herhangi bir Hilbert uzayının düzgün konveks bir Banach uzayı olduğunu ima eder .

En iyi yaklaşım

Bu alt bölüm Hilbert izdüşüm teoremini kullanır . Eğer Cı- Hilbert alan bir boş olmayan kapalı konveks alt kümesi , H ve x bir noktaya H , benzersiz bir nokta da mevcuttur y ∈ Cı bu en aza indirir arasındaki mesafe x ve nokta C ,

${\displaystyle y\in C\,,\quad \|xy\|=\operatör adı {dist} (x,C)=\min\{\|xz\|:z\in C\}\,.}$

Bu, çevrilmiş dışbükey D = C - x kümesinde minimum normlu bir nokta olduğunu söylemekle eşdeğerdir . Kanıt, her minimizasyon dizisinin ( d _n ) ⊂ D' nin Cauchy olduğunu (paralelkenar özdeşliğini kullanarak) dolayısıyla D' de minimum norma sahip bir noktaya (tamlığı kullanarak) yakınsadığını göstermekten ibarettir . Daha genel olarak, bu herhangi bir düzgün dışbükey Banach uzayında geçerlidir.

Bu sonuç, bir kapalı alt uygulandığında F arasında H , nokta, gösterilebilir y ∈ F yakın x ile karakterize edilir

${\displaystyle y\in F\,,\quad xy\perp F\,.}$

Bu nokta y olan dik izdüşüm ve x üzerine F ve eşleme P _F  : X → Y doğrusaldır (bkz Ortogonal tamamlar ve çıkıntıları ). Bu sonuç, özellikle en küçük kareler yöntemlerinin temelini oluşturduğu uygulamalı matematikte , özellikle sayısal analizde önemlidir .

Özellikle, F , H'ye eşit olmadığında , F'ye ortogonal v sıfır olmayan bir vektör bulunabilir ( x ∉ F ve v = x − y seçin ). Bu gözlem , H'nin bir S alt kümesi tarafından üretilen kapalı F altuzayına uygulanarak çok yararlı bir kriter elde edilir .

Bir alt G arasında H vektörü 0 tek vektörüdür (ve sadece) ise yoğun bir vektör altuzaya yayılan V ∈ H ortogonal S .

ikilik

İkili uzay H * Her alandır sürekli uzay gelen lineer fonksiyonların H taban alanına. tarafından tanımlanan doğal bir norm taşır.

${\displaystyle \|\varphi \|=\sup _{\|x\|=1,x\in H}|\varphi (x)|\,.}$

Bu norm paralelkenar yasasını karşılar ve dolayısıyla ikili uzay aynı zamanda bir iç çarpım uzayıdır ve bu iç çarpım polarizasyon özdeşliği kullanılarak bu ikili norm açısından tanımlanabilir . İkili uzay da tamdır, yani kendi başına bir Hilbert uzayıdır. Eğer e _• = ( e _i ) _{i ∈ I} , H için tam bir ortonormal taban ise, o zaman herhangi ikisinin ikili uzayındaki iç çarpım şudur: ${\displaystyle f,g\in H^{*}}$

${\displaystyle \langle f,g\rangle _{H^{*}}=\sum _{i\in I}f(e_{i}){\overline {g(e_{i})}}}$

burada bu dizideki terimlerin çoğu hariç hepsi sıfırdır.

Riesz teoremi ikili alan uygun bir tanım verir. Her elemana u arasında H , eşsiz bir unsur olduğunu φ _u ait H * , tarafından tanımlanan

${\displaystyle \varphi _{u}(x)=\langle x,u\rangle \,}$

ayrıca nerede, ${\displaystyle \sol\|\varphi _{u}\sağ\|=\sol\|u\sağ\|.}$

Haritayı o Riesz teoremi devletler H için H * ile tanımlanan u dönderilirlerse j _u olan örten bu harita bir hale getiren izometrik antilinear izomorfizm. Yani her eleman için cp ikili arasında H * Bir ve sadece bir tane var u _j in H şekilde

${\displaystyle \langle x,u_{\varphi }\rangle =\varphi (x)}$

tüm x ∈ H için . İkili boşluk H * üzerindeki iç çarpım aşağıdakileri karşılar:

${\displaystyle \langle \varphi ,\psi \rangle =\langle u_{\psi },u_{\varphi }\rangle \,.}$

Sağ taraftaki geri yükler doğrusal düzeninin üzerinde ters cp arasında antilinearity gelen u _j . Gerçek bir durumda, gelen antilinear izomorfizm H onun ikili aslında bir izomorfizması olduğunu ve bu nedenle gerçek Hilbert uzayları kendi ikililere doğal izomorfik.

Temsil eden vektör u _φ aşağıdaki şekilde elde edilir. Tüm φ ≠ 0 , çekirdek F = Ker ( φ ) kapalı bir vektör alt uzay olan H , değil eşit H dolayısıyla sıfır olmayan bir vektör vardır, hacim için ortogonal F . u vektörü , v'nin uygun bir skaler katı λv'dir . Uygun olduğu veya φ ( v ) = ⟨ v , u ⟩ verimler

${\displaystyle u=\langle v,v\rangle ^{-1}\,{\overline {\varphi (v)}}\,v\,.}$

Bu φ ↔ u denkliği , fizikte popüler olan bra-ket notasyonundan yararlanılır . Fizikte, ⟨ x | y ⟩ , sağda doğrusaldır,

${\displaystyle \langle x|y\rangle =\langle y,x\rangle \,.}$

Sonuç ⟨ x | y ⟩ lineer fonksiyonel ⟨ x | ( sütyen ) vektör üzerinde | y ⟩ ( ket ).

Riesz temsil teoremi temelde sadece bir iç çarpımın varlığına değil, aynı zamanda uzayın bütünlüğüne de dayanır. Aslında teorem , herhangi bir iç çarpım uzayının topolojik dualinin , onun tamamlanmasıyla tanımlanabileceğini ima eder . Riesz temsil teoremi dolaysız bir sonucu, bir Hilbert uzayı o da H olan dönüşlü doğal haritası, yani H onun içine çift çift boşluk bir izomorfizması olduğunu.

Zayıf yakınsak diziler

Bir Hilbert alanı içinde H , bir sekans { x _{, n} } olan zayıf yakınsayan bir vektör x ∈ H olduğunda

${\displaystyle \lim _{n}\langle x_{n},v\rangle =\langle x,v\rangle }$

her v ∈ H için .

Örneğin, herhangi bir ortonormal dizi { f _n } , Bessel eşitsizliğinin bir sonucu olarak zayıf bir şekilde 0'a yakınsar . Her zayıf yakınsak dizi { x _n } , düzgün sınırlılık ilkesiyle sınırlıdır .

Tersine, Hilbert uzayındaki her sınırlı dizi, zayıf yakınsak alt dizileri kabul eder ( Alaoğlu teoremi ). Bu durum sürekli olarak en aza indirilmesi sonucu kanıtlamak için kullanılabilmektedir dışbükey fonksiyonellerin aynı şekilde, Bolzano sıkıştırma teoremi sürekli fonksiyonlar için kullanılan R, ^d . Çeşitli varyantlar arasında basit bir ifade aşağıdaki gibidir:

Eğer f  : H → R bir dışbükey sürekli fonksiyon şekildedir f ( x ) eğilimi + ∞ zaman || x || ∞ eğilimindedir , o zaman f , x ₀ ∈ H bir noktasında bir minimum kabul eder .

Bu gerçek (ve çeşitli genellemeleri) , varyasyon hesabındaki doğrudan yöntemler için temeldir . Konveks fonksiyonellerde için en aza indirilmesi sonucu Hilbert uzayında dışbükey alt kümeleri sınırlı kapalı biraz daha soyut aslında doğrudan bir sonucu da , H olan zayıf kompakt olduğundan, H dönüşlüdür. Zayıf yakınsak alt dizilerin varlığı, Eberlein-Šmulian teoreminin özel bir durumudur .

Banach uzayı özellikleri

Banach uzaylarının herhangi bir genel özelliği Hilbert uzayları için geçerli olmaya devam eder. Açık dönüşüm teoremi bir o devletler sürekli örten bir Banach uzayı diğerine doğrusal dönüşüm bir olduğunu açık haritalama açık setleri açık kümeleri gönderir anlamına gelir. Doğal bir sonucu, bir teoremi ters sınırlanan bir sürekli ve bu, örten (olduğunu, olan ters, bir devamlı doğrusal harita sürekli da olan) bir Banach uzaydan bir doğrusal fonksiyonu, izomorfizm olup. Bu teoremi, Hilbert uzayları durumunda kanıtlamak, genel Banach uzaylarından çok daha basittir. Açık eşleme teoremi, bir Banach uzayından diğerine doğrusal bir fonksiyonun, ancak ve ancak grafiğinin kapalı bir küme olması durumunda sürekli olduğunu iddia eden kapalı grafik teoremine eşdeğerdir . Hilbert uzayları durumunda, bu sınırsız operatörlerin çalışmasında temeldir (bkz. kapalı operatör ).

(Geometrik) Hahn-Banach teoremi , kapalı bir dışbükey kümenin , Hilbert uzayının bir hiperdüzlemi aracılığıyla dışındaki herhangi bir noktadan ayrılabileceğini iddia eder . Bu, en iyi yaklaşıklık özelliğinin doğrudan bir sonucudur : y , x'e en yakın kapalı konveks F kümesinin elemanıysa , o zaman ayırıcı hiperdüzlem, orta noktasından geçen xy doğru parçasına dik olan düzlemdir .

Hilbert uzaylarında operatörler

Sınırlı operatörler

Sürekli lineer operatörler A  : 'H ₁ → H ₂ Hilbert boşluğundan H ₁ , ikinci Hilbert alanı için H ₂ edilir sınırlı eşleştikleri anlamda sınırlı setleri sınırlı kümelerine. Tersine, bir operatör sınırlıysa, o zaman süreklidir. Bu tür sınırlı lineer operatörlerin uzayının bir normu vardır , operatör normu şu şekilde verilir:

${\displaystyle \lVert A\rVert =\sup \left\{\,\lVert Ax\rVert :\lVert x\rVert \leq 1\,\right\}\,.}$

İki sınırlı doğrusal operatörün toplamı ve bileşimi yine sınırlı ve doğrusaldır. İçin y olarak H ₂ gönderir harita x ∈ H ₁ için ⟨ Ax , y ⟩ doğrusal ve sürekli ve uygun olan Riesz teoremi nedenle şeklinde temsil edilebilir:

${\displaystyle \sol\langle x,A^{*}y\sağ\rangle =\langle Ax,y\rangle }$

Bazı vektör için bir * y olarak H ₁ . Bu tanımlar başka sınırlı lineer operatör bir *: H ₂ → H ₁ , eşlenik bir A . Ek, A ** = A'yı sağlar . Riesz teoremi sürekli çift boşluk her Hilbert boşluk tanımlamak için kullanıldığı zaman, bir eşlenik A olduğu gösterilebilir özdeş devrik ^t A  : H ₂ * → H ₁ * ve A tanım olarak gönderir için işlevsel${\displaystyle \psi \in H_{2}^{*}}$${\displaystyle \psi \circ A\in H_{1}^{*}.}$

Grubu B ( H ) tüm sınırlı lineer operatörlerin H (yani operatörler H → H birlikte ilavesi ve bileşimin operasyonları ile), norm ve eşlenik işlemi, a, Cı * cebiri türüdür, operatör cebir .

A * = A ise , B( H ) 'nin bir A elemanına 'kendi kendine eş' veya 'Hermityen' denir . Eğer bir Hermisyen ve bir ⟨ Ax , X ⟩ ≥ 0 , her için x , daha sonra bir 'negatif olmayan', yazılı olarak adlandırılan bir ≥ 0 ; eşitlik yalnızca x = 0 olduğunda geçerliyse , A'ya 'pozitif' denir. Kendine eşlenik operatörlerinin grubu, bir kabul kısmi düzeni olup, burada bir ≥ B ise A - B ≥ 0 . Eğer bir formu vardır B * B bazı B , daha sonra bir negatif olmayan olduğu; eğer B ters çevrilebilir olup, daha sonra bir pozitiftir. Bir tersinin de negatif olmayan bir operatör için, bir anlamda doğrudur A , benzersiz negatif olmayan vardır karekök B öyle

${\displaystyle A=B^{2}=B^{*}B\,.}$

Spektral teoremin kesinleştirdiği bir anlamda , kendine-eşlenik operatörler faydalı bir şekilde "gerçek" operatörler olarak düşünülebilir. Bir eleman A ve B ( H ) olarak adlandırılır , normal durumunda bir * A = AA * . Normal operatörler, kendine eşlenik operatörlerin toplamına ve kendine eşleşik operatörün sanal katının toplamına ayrışır.

${\displaystyle A={\frac {A+A^{*}}{2}}+i{\frac {AA^{*}}{2i}}}$

birbirleriyle gidip gelenler. Normal operatörler, gerçek ve sanal kısımları açısından da faydalı bir şekilde düşünülebilir.

Bir eleman U arasında B ( H ) olarak adlandırılan birim , eğer U tersinirdir ve tersi, aşağıdakiyle verilir U * . Bu aynı zamanda gerektirerek ifade edilebilir U üzerine olabilir ve ⟨ Ux , Uy ⟩ = ⟨ x , y ⟩ tüm x , y ∈ H . Üniter operatörler , H'nin izometri grubu olan bileşim altında bir grup oluşturur .

Bir elemanı B ( H ) olan kompakt bu için bir ön set gönderirse nispeten kompakt kümeleri. Eşdeğer olarak, herhangi bir sınırlı dizi { x _k } için , { Tx _k } dizisinin yakınsak bir altdizisi varsa, sınırlı bir operatör T kompakttır . Birçok integral operatör kompakttır ve aslında Hilbert-Schmidt operatörleri olarak bilinen ve özellikle integral denklemlerinin çalışmasında önemli olan özel bir operatör sınıfını tanımlar . Fredholm operatörleri , bir kompakt operatörden kimliğin katları ile farklılık gösterir ve eşdeğer olarak, sonlu boyutlu çekirdeğe ve kokernel'e sahip operatörler olarak karakterize edilir . Bir Fredholm operatörünün T indeksi şu şekilde tanımlanır:

${\displaystyle \operatöradı {index} T=\dim \ker T-\dim \operatöradı {coker} T\,.}$

İndeks homotopi değişmezdir ve Atiyah-Singer indeks teoremi aracılığıyla diferansiyel geometride derin bir rol oynar .

Sınırsız operatörler

Sınırsız operatörler Hilbert uzaylarında da izlenebilir ve kuantum mekaniği için önemli uygulamalara sahiptir . Bir Hilbert uzayı H üzerindeki bir sınırsız T operatörü, D ( T ) alanı H'nin bir lineer alt uzayı olan lineer bir operatör olarak tanımlanır . Genellikle D ( T ) alanı , H'nin yoğun bir alt uzayıdır, bu durumda T , yoğun tanımlanmış bir operatör olarak bilinir .

Yoğun olarak tanımlanmış sınırsız bir operatörün eki, esasen sınırlı operatörlerle aynı şekilde tanımlanır. Kendine eş sınırsız operatörler , kuantum mekaniğinin matematiksel formülasyonunda gözlenebilirlerin rolünü oynarlar . Hilbert uzayı L ² ( R ) üzerindeki kendinden eşlenik sınırsız operatörlerin örnekleri şunlardır:

• Diferansiyel operatörünün uygun bir uzantısı
  $${\displaystyle (Af)(x)=-i{\frac {\mathrm {d} }{\mathrm {d} x}}f(x)\,,}$$

  
  burada i sanal birim ve f kompakt desteğin türevlenebilir bir fonksiyonudur.
• x ile çarpma operatörü:
  $${\görüntüleme stili (Bf)(x)=xf(x)\,.}$$

  

Bunlar sırasıyla momentum ve konum gözlemlenebilirlerine karşılık gelir. Ne A ne de B'nin H'nin tamamında tanımlı olmadığına dikkat edin , çünkü A durumunda türevin var olması gerekmez ve B durumunda çarpım fonksiyonunun kare integrallenebilir olması gerekmez. Her iki durumda da, olası bağımsız değişkenler grubu yoğun alt uzay oluşturan L ² ( R ) .

İnşaatlar

Doğrudan toplamlar

İki Hilbert uzayı H ₁ ve H ₂ , (ortogonal) doğrudan toplam adı verilen ve ile gösterilen başka bir Hilbert uzayında birleştirilebilir.

${\displaystyle H_{1}\oplus H_{2}\,,}$

Tüm grubu aşağıdakilerden oluşan sıralı çiftleri ( x ₁ , x ₂ ) burada X _i ∈ H _ı , i , 1 = 2 ve iç ürün tarafından tanımlanan

${\displaystyle {\bigl \langle }(x_{1},x_{2}),(y_{1},y_{2}){\bigr \rangle }_{H_{1}\oplus H_{2} }=\left\langle x_{1},y_{1}\right\rangle _{H_{1}}+\left\langle x_{2},y_{2}\right\rangle _{H_{2} }\,.}$

Daha genel olarak, eğer H _i , i ∈ I tarafından indekslenen Hilbert uzaylarının bir ailesiyse , o zaman H _i'nin doğrudan toplamı ile gösterilir.

${\displaystyle \bigoplus _{i\in I}H_{i}}$

dizine alınmış tüm ailelerin kümesinden oluşur

${\displaystyle x=(x_{i}\in H_{i}|i\in I)\in \prod _{i\in I}H_{i}}$

içinde Kartezyen ürün arasında H _I şekilde

${\displaystyle \sum _{i\in I}\|x_{i}\|^{2}<\infty \,.}$

İç çarpım şu şekilde tanımlanır:

${\displaystyle \langle x,y\rangle =\sum _{i\in I}\left\langle x_{i},y_{i}\right\rangle _{H_{i}}\,.}$

Her biri, H, _I , tüm direkt toplamında bir kapalı alt olarak dahil edilir , H _ı . Ayrıca, H _i ikili olarak ortogonaldir. Kapalı Altuzayların bir sistem, varsa Tersine, V _i , i ∈ I bir Hilbert uzayı içinde, H ikişerli ortogonal olan ve sendika yoğun olduğundan, H , daha sonra H doğrudan toplamına canonically izomorftur V _i . Bu durumda H , V _i'nin dahili doğrudan toplamı olarak adlandırılır . (İç veya dış) bir direk toplam de ortogonal çıkıntılar bir aile ile donatılmıştır E _ı üzerine I inci doğrudan toplam kısmı H _i . Bu projeksiyonlar, kendine eş, sınırlanan İdempotent dikgenlik şartını operatörleri

${\displaystyle E_{i}E_{j}=0,\quad i\neq j\,.}$

Spektral teoremi için kompakt bir Hilbert alanı üzerinde özeslenik operatörleri H olduğu durumları , H , bir operatörün Aygen ortogonal bir doğrudan toplamı halinde böler, ve aynı zamanda Aygen üzerine çıkıntıların bir toplamı olarak operatör açık bir ayrışmasını sağlar. Hilbert uzaylarının doğrudan toplamı, kuantum mekaniğinde, değişken sayıda parçacık içeren bir sistemin Fock uzayı olarak da görünür ; burada, doğrudan toplamdaki her Hilbert uzayı , kuantum mekanik sistem için ek bir serbestlik derecesine karşılık gelir . In temsil teorisi , Peter-Weyl teoremi garanti herhangi üniter temsili a kompakt grubunun sonlu boyutlu temsiller direkt toplamı olarak bir Hilbert uzayı bölünme üzerine.

Tensör ürünleri

Eğer x _{, 1} , y ₁ ε H ₁ ve x ₂ , y ₂ ε H ₂ , (olağan) daha sonra bir nolu bir iç ürün tensör ürünü aşağıdaki gibi. On basit tensörlerinin , let

${\displaystyle \langle x_{1}\otimes x_{2},\,y_{1}\otimes y_{2}\rangle =\langle x_{1},y_{1}\rangle \,\langle x_{ 2},y_{2}\rangle \,.}$

Bu formül, daha sonra uzanır sesquilinearity bir iç ürüne H ₁ ⊗ H ₂ . H ₁ ve H ₂ 'nin bazen H ₁ H ₂${\ Displaystyle {\widehat {\otimes }}}$ ile gösterilen Hilbert tensör ürünü, bu iç çarpımla ilişkili metrik için H ₁ ⊗ H ₂ tamamlanarak elde edilen Hilbert uzayıdır .

Hilbert uzayı L ² ([0, 1]) tarafından bir örnek verilmiştir . İki kopya Hilbertian tensör ürün L ² ([0, 1]), izometrik olarak ve doğrusal izomorfik alanı olan L ² ([0, 1] ² ) kare kare integrallenebilen fonksiyonların [0, 1] ² . Bu izomorfizm , fonksiyona basit bir tensör f ₁ ⊗ f ₂ gönderir

${\displaystyle (s,t)\mapsto f_{1}(s)\,f_{2}(t)}$

meydanda.

Bu örnek aşağıdaki anlamda tipiktir. Her basit tensör çarpımı ile ilişkili x ₁ ⊗ x ₂ , H'den birinci derece operatördür.^∗
₁için H ₂ Verilen eşler x * ∈ H^∗
₁ olarak

${\displaystyle x^{*}\mapsto x^{*}(x_{1})x_{2}\,.}$

Basit tensörlerle tanımlanan Bu eşleme arasında doğrusal bir tanımlama uzanan H ₁ ⊗ H ₂ ve sonlu seviye operatörlerin alan H^∗
₁için H ₂ . Bu, Hilbert tensör ürünü H ₁ H _2'nin${\ Displaystyle {\widehat {\otimes }}}$ Hilbert uzayı HS ( H^∗
₁, H ₂ ) arasında Hilbert Schmidt operatörleri arasından H^∗
₁için H ₂ .

ortonormal bazlar

Lineer cebirden bir ortonormal taban kavramı Hilbert uzayları durumuna genellenir. Bir Hilbert uzayında H , bir ortonormal taban, koşulları sağlayan H elemanlarının bir { e _k } _{k ∈ B} ailesidir :

1. Ortogonallik : B'nin her iki farklı elemanı ortogonaldir: ⟨ e _k , e _j ⟩ = 0 k ≠ j ile tüm k , j ∈ B için .
2. Normalleştirme : Ailenin her elemanının normu 1 vardır: || e _k || = 1 tüm k ∈ B için .
3. Tamlığı : doğrusal yayılma aile içinde e _k , k ∈ B , olduğu yoğun içinde H .

İlk iki koşul temel tatmin edici vektörlerin bir sistem ortonormal sistemi veya ortonormal grubu (ya da eğer ortonormal dizi denir B olan sayılabilir ). Böyle bir sistem her zaman lineer bağımsızdır . Bir Hilbert uzayının bir ortonormal vektör sisteminin tamlığı eşdeğer olarak şu şekilde yeniden ifade edilebilir:

Eğer ⟨ v , e _k ⟩ = 0 tüm k ∈ B ve bazı v ∈ H sonra v = 0 .

Bu durum ile ilgilidir, sadece vektör ortogonal yoğun lineer alt uzayı sıfır vektör, eğer söz konusu G bir ortonormal seti ve V dik olan S , daha sonra hacim doğrusal yayılma kapatılması ortogonal olan S , burada tüm uzaydır.

Ortonormal bazların örnekleri şunları içerir:

• grubu {(1, 0, 0), (0, 1, 0), (0, 0, 1)}, bir ortonormal oluşturan R ³ ile nokta ürün ;
• f _n ( x ) = exp (2π inx ) ile { f _n  : n ∈ Z } dizisi L ² ([0, 1]) karmaşık uzayının bir ortonormal tabanını oluşturur ;

Sonsuz boyutlu durumda, bir ortonormal temel lineer cebir anlamında bir temel olmayacaktır ; ikisini ayırt etmek için ikinci temele Hamel temeli de denir . Temel vektörlerin açıklığının yoğun olması, uzaydaki her vektörün sonsuz bir serinin toplamı olarak yazılabileceğini ve diklik, bu ayrıştırmanın benzersiz olduğunu ima eder.

sıra uzayları

Karmaşık sayıların kare toplanabilir dizilerinin uzayı , sonsuz dizilerin kümesidir. ${\ Displaystyle \ _{2}}$

${\displaystyle (c_{1},c_{2},c_{3},\dots )}$

gerçek veya karmaşık sayıların

${\displaystyle \left|c_{1}\right|^{2}+\left|c_{2}\right|^{2}+\left|c_{3}\right|^{2}+\cdots <\infty\,.}$

Bu uzayın ortonormal bir tabanı vardır:

${\displaystyle {\begin{aligned}e_{1}&=(1,0,0,\dots )\\e_{2}&=(0,1,0,\dots )\\&\ \ \vdots \end{hizalanmış}}}$

Bu uzay, sonlu boyutlu vektörlerin uzayının sonsuz boyutlu genellemesidir . Genellikle sonsuz boyutlu uzaylarda, kapalı ve sınırlı bir kümenin (tüm sonlu boyutlu uzaylarda olduğu gibi ) (sıralı olarak) kompakt olmadığını göstermek için kullanılan ilk örnektir . Gerçekten de, yukarıdaki ortonormal vektörler kümesi şunu gösterir: Birim toptaki vektörlerin sonsuz bir dizisidir (yani, normu birden küçük veya ona eşit olan puanlar topu). Bu küme açıkça sınırlı ve kapalıdır; yine de, bu vektörlerin hiçbir ardışıklığı herhangi bir şeye yakınsar ve sonuç olarak birim top kompakt değildir. Sezgisel olarak bunun nedeni, dizinin sonraki öğelerinin kaçabileceği "her zaman başka bir koordinat yönü vardır". ${\ Displaystyle \ _{2}^{n}}$${\ Displaystyle \ _{2}}$

Alanı birçok yönden genelleştirebiliriz . Örneğin, eğer B herhangi bir (sonsuz) küme ise, o zaman şu şekilde tanımlanan B indeks kümesine sahip dizilerin Hilbert uzayı oluşturulabilir . ${\ Displaystyle \ _{2}}$

${\displaystyle \ell ^{2}(B)=\left\{x:B{\xrightarrow {x}}\mathbb {C} \,\left|\,\sum _{b\in B}\left |x(b)\sağ|^{2}<\infty \sağ.\sağ\}\,.}$

B üzerinden toplam burada tanımlanır

${\displaystyle \sum _{b\in B}\left|x(b)\right|^{2}=\sup \sum _{n=1}^{N}\left|x(b_{n} )\doğru|^{2}}$

sup tüm sonlu alt kümelerinin üzerine atılıyor  B . Bu toplamın sonlu olması için, l ² ( B )' nin her elemanının yalnızca sayılabilir sayıda sıfır olmayan terime sahip olduğu sonucu çıkar. Bu uzay iç çarpım ile bir Hilbert uzayı olur.

${\displaystyle \langle x,y\rangle =\sum _{b\in B}x(b){\overline {y(b)}}}$

tüm x , y ∈ l ² ( B ) için . Burada toplamın sadece sayılabilir sıfır olmayan terimleri vardır ve Cauchy-Schwarz eşitsizliği tarafından koşulsuz olarak yakınsaktır.

l ² ( B )' nin bir ortonormal tabanı , tarafından verilen B kümesi tarafından indekslenir .

${\displaystyle e_{b}(b')={\begin{durumlar}1&{\text{if }}b=b'\\0&{\text{aksi halde.}}\end{durumlar}}}$

Bessel eşitsizliği ve Parseval formülü

Let f ₁ , ..., f _n sonlu ortonormal sistem olmak  H . Keyfi bir vektör x ∈ H için , izin verin

${\displaystyle y=\sum _{j=1}^{n}\langle x,f_{j}\rangle \,f_{j}\,.}$

Sonra her k = 1, ..., n için ⟨ x , f _k ⟩ = ⟨ y , f _k ⟩ . İzler , x - y , her ortogonal olan ön _k nedenle, X - Y dik olan  y . Pisagor özdeşliğini iki kez kullanarak, şunu takip eder:

${\displaystyle \|x\|^{2}=\|xy\|^{2}+\|y\|^{2}\geq \|y\|^{2}=\sum _{j= 1}^{n}{\bigl |}\langle x,f_{j}\rangle {\bigr |}^{2}\,.}$

Let { f _i }, i ∈ I , rasgele bir ortonormal sistemi olabilir  H . Her sonlu alt kümesi için önceki eşitsizliği uygulanması J ait I Bessel eşitsizliği verir:

${\displaystyle \sum _{i\in I}{\bigl |}\langle x,f_{i}\rangle {\bigr |}^{2}\leq \|x\|^{2},\quad x\in H}$

( negatif olmayan gerçek sayıların keyfi bir ailesinin toplamının tanımına göre ).

Geometrik olarak, Bessel eşitsizliği ortogonal projeksiyonu ifade eder , x , doğrusal matrisini tarafından gerilen f _ı o aşmayan sahip norm x . İki boyutta, bu, bir dik üçgenin bacak uzunluğunun hipotenüsün uzunluğunu aşamayabileceği iddiasıdır.

Bessel'in eşitsizliği, Bessel'in eşitsizliğinin aslında bir eşitlik olduğu durumu yöneten Parseval'in kimliği olarak adlandırılan daha güçlü sonuca giden bir basamak taşıdır . Tanım gereği, { e _k } _{k ∈ B} ortonormal baz olan , H , daha sonra her eleman X ve H olarak yazılabilir

${\displaystyle x=\sum _{k\in B}\sol\langle x,e_{k}\sağ\rangle \,e_{k}\,.}$

B sayılamayan olsa bile , Bessel'in eşitsizliği, ifadenin iyi tanımlı olduğunu ve yalnızca sayılabilir çok sayıda sıfır olmayan terimden oluştuğunu garanti eder. Bu toplam, x'in Fourier açılımı olarak adlandırılır ve bireysel katsayılar ⟨ x , e _k ⟩ , x'in Fourier katsayılarıdır . Parseval'in kimliği daha sonra şunu iddia ediyor:

${\displaystyle \|x\|^{2}=\sum _{k\in B}|\langle x,e_{k}\rangle |^{2}\,.}$

Tersine, eğer { e _k } , Parseval'in özdeşliği her x için geçerli olacak şekilde bir ortonormal küme ise , o zaman { e _k } bir ortonormal tabandır.

Hilbert boyutu

Zorn lemmasının bir sonucu olarak , her Hilbert uzayı bir ortonormal temeli kabul eder; ayrıca, aynı uzayın herhangi iki ortonormal tabanı, uzayın Hilbert boyutu olarak adlandırılan aynı kardinaliteye sahiptir . Örneğin, l ² ( B ) , B tarafından endekslenen bir ortonormal tabana sahip olduğundan, Hilbert boyutu B'nin kardinalitesidir (bu sonlu bir tamsayı veya sayılabilir veya sayılamayan bir ana sayı olabilir ).

Parseval'ın kimliğinin bir sonucu olarak, eğer { e _k } _{k ∈ B} ortonormal baz olan H sonra harita, : Φ H → l ² ( B ) ile tanımlanan cp ( x ) = ⟨x, e _k ⟩ _{k ∈ B} Hilbert uzaylarının izometrik bir izomorfizmidir: öyle bir çift yönlü doğrusal haritalamadır

${\displaystyle {\bigl \langle }\Phi (x),\Phi (y){\bigr \rangle }_{l^{2}(B)}=\left\langle x,y\right\rangle _ {H}}$

tüm x , y ∈ H için . Asılsayı ait B Hilbert boyutudur H . Bu nedenle, her Hilbert alan bir sekans alanı için izometrik izomorf l ² ( B ), bir resim için B .

Ayrılabilir boşluklar

Tanım olarak, yoğun bir sayılabilir alt küme içermesi koşuluyla bir Hilbert uzayı ayrılabilirdir . Zorn'un lemması ile birlikte bu, Hilbert uzayının sadece ve ancak sayılabilir bir ortonormal temeli kabul etmesi durumunda ayrılabilir olduğu anlamına gelir . Tüm sonsuz boyutlu ayrılabilir Hilbert uzayları bu nedenle izometrik olarak l ^{2 ile} izomorfiktir .

Geçmişte, Hilbert uzaylarının tanımın bir parçası olarak ayrılabilir olması gerekiyordu. Fizik kullanılan çoğu alanlarda ayrılabilir, ve bu birbirine tüm izomorfik olduğu için, sık sık "gibi herhangi bir sonsuz boyutlu ayrılabilir Hilbert alanı gösterir Hilbert alan" ya da sadece "Hilbert alan". Kuantum alan teorisinde bile , Wightman aksiyomlarının şart koştuğu gibi, Hilbert uzaylarının çoğu aslında ayrılabilirdir . Bununla birlikte, bazen ayrılamayan Hilbert uzaylarının kuantum alan teorisinde de önemli olduğu tartışılır, çünkü teorideki sistemler sonsuz sayıda serbestlik derecesine ve herhangi bir sonsuz Hilbert tensör ürününe (birden büyük boyutlu uzayların) sahip olduğu için. ayrılmaz. Örneğin, bir bozonik alan , doğal olarak, faktörleri uzayın her noktasında harmonik osilatörleri temsil eden bir tensör ürününün bir öğesi olarak düşünülebilir. Bu perspektiften, bir bozonun doğal durum uzayı, ayrılamaz bir uzay gibi görünebilir. Ancak, fiziksel olarak anlamlı alanlar (üzerinde gözlemlenebilirlerin tanımlanabileceği) içerebilen, tam tensör çarpımının yalnızca küçük bir ayrılabilir alt uzayıdır. Ayrılamayan başka bir Hilbert uzayı, uzayın sınırsız bir bölgesindeki sonsuz parçacık koleksiyonunun durumunu modeller. Uzayın bir ortonormal temeli, parçacıkların yoğunluğu tarafından endekslenir, sürekli bir parametredir ve olası yoğunluklar kümesi sayılamadığından, taban sayılabilir değildir.

Ortogonal tamamlayıcılar ve projeksiyonlar

Eğer S Hilbert alan bir alt kümesi , H , vektörler grubu ortogonal S ile tanımlanır

${\displaystyle S^{\perp }=\left\{x\in H:\langle x,s\rangle =0\ {\text{ tüm }}s\in S\right\}\,.}$

Grubu S ^⊥ a, kapalı bir alt uzay H (iç ürünün doğrusallığını ve sürekliliği ile kolayca ispat edilebilir) ve form kendisi Hilbert alanı çok. Eğer V bir kapalı alt uzay olan H , sonra V ^⊥ adlandırılan ortogonal tamamlayıcı bir V . Aslında, her x ∈ H daha sonra v ∈ V ve w ∈ V ^⊥ ile x = v + w olarak benzersiz bir şekilde ^yazılabilir . Bu nedenle, H , V ve V ^⊥'nin Hilbert'in dahili doğrudan toplamıdır .

Doğrusal operatör P _V  : H → H haritalar x için v denir ortogonal projeksiyonu üzerine V . Bir vardır doğal tüm kapalı bölme odasının grubu arasında bire bir karşılık H ve sınırlı kendine eşlenik operatörler grubu P , öyle ki p ² = p . özellikle,

Bu, P _V ( x )' in geometrik yorumunu sağlar : V'nin elemanları tarafından x'e en iyi yaklaşımdır .

P _U P _V = 0 ise, P _U ve P _V projeksiyonları karşılıklı olarak dik olarak adlandırılır . Bu, U ve V'nin H'nin alt uzayları olarak ortogonal olmasına eşdeğerdir . P _U ve P _V iki projeksiyonunun toplamı, yalnızca U ve V birbirine dik ise ve bu durumda P _U + P _V = P _{U + V} ise bir projeksiyondur . Bileşik P _U P _V genellikle bir izdüşüm değildir; aslında bileşik, ancak ve ancak iki izdüşüm yer değiştiriyorsa ve bu durumda P _U P _V = P _{U ∩ V} ise bir izdüşümdür .

Kod bölgesini Hilbert uzayı V ile sınırlayarak, ortogonal izdüşüm P _V bir izdüşüm eşlemesine yol açar π  : H → V ; bu, dahil etme eşlemesinin ekidir

${\displaystyle i:V\to H\,,}$

anlamında

${\displaystyle \sol\langle ix,y\sağ\rangle _{H}=\sol\langle x,\pi y\right\rangle _{V}}$

tüm x ∈ V ve y ∈ H için .

Sıfırdan farklı bir kapalı altuzay V üzerine dik izdüşüm P _V'nin operatör normu 1'e eşittir:

${\displaystyle \|P_{V}\|=\sup _{x\in H,x\neq 0}{\frac {\|P_{V}x\|}{\|x\|}}=1 \,.}$

Bir Hilbert uzayının her kapalı V alt uzayı bu nedenle, P ² = P olacak şekilde bir normun P operatörünün görüntüsüdür . Uygun izdüşüm operatörlerine sahip olma özelliği Hilbert uzaylarını karakterize eder:

• 2'den daha yüksek boyut Banah alanı (izometrik) her kapalı alt uzay için Hilbert alan, ancak ve ancak, bir V , bir operatör vardır p _V normu bir görüntü ait V , öyle ki p²
  _V= P _V .

Bu sonuç bir Hilbert uzayının metrik yapısını karakterize ederken, bir topolojik vektör uzayı olarak bir Hilbert uzayının yapısı , tamamlayıcı alt uzayların varlığı açısından karakterize edilebilir:

• Banah alan X, ancak ve ancak, her kapalı alt uzay eğer Hilbert boşluğa topolojik ve doğrusal izomorf V , kapalı bir alt uzay vardır W şekilde X, iç direk toplam eşittir V ⊕ W .

Ortogonal tamamlayıcı, bazı daha temel sonuçları karşılar. Bu bir monoton fonksiyonu anlamda, eğer U ⊂ V , daha sonra V ^⊥ ⊆ U ^⊥ eşitlik tutma ile, ancak ve ancak, eğer V içerdiği kapağın arasında U . Bu sonuç, Hahn-Banach teoreminin özel bir durumudur . Bir alt uzayın kapanması, ortogonal tümleyen açısından tamamen karakterize edilebilir: eğer V , H'nin bir alt uzayı ise , o zaman V'nin kapanması eşittir V ^⊥⊥ . Ortogonal tamamlayıcı böylece olan Galois'in bağlantısı ile kısmi amacıyla Hilbert alan bölme odasının. Genel olarak, bir alt uzay toplamının ortogonal tümleyeni, ortogonal tümleyenlerin kesişimidir:

${\displaystyle \left(\sum _{i}V_{i}\sağ)^{\perp }=\bigcap _{i}V_{i}^{\perp }\,.}$

Eğer V _i ek olarak, daha sonra kapatılır

${\displaystyle {\overline {\sum _{i}V_{i}^{\perp }}}=\left(\bigcap _{i}V_{i}\sağ)^{\perp }\,.}$

spektral teori

Hilbert uzayında kendine eşlenik operatörler için iyi geliştirilmiş bir spektral teori vardır ; bu, gerçekler üzerinde simetrik matrislerin veya karmaşık sayılar üzerinde kendine bitişik matrislerin çalışmasına kabaca benzer . Aynı anlamda, ortogonal izdüşüm operatörlerinin uygun bir toplamı (aslında bir integral) olarak kendine eşlenik bir operatörün bir "köşegenleştirilmesi" elde edilebilir.

Bir operatör spektrumu T ile gösterilen σ ( T ) , karmaşık sayılar kümesidir λ şekilde T - λ sürekli ters yoksundur. Eğer T sınırlanan, daha sonra spektrum her zaman olduğu kompakt kümesi kompleks düzlemde ve diskin içinde yalanlar | z | ≤ || T || . Eğer T kendine eş ise, spektrum gerçektir. Aslında, [ m , M ] aralığında yer alır , burada

${\displaystyle m=\inf _{\|x\|=1}\langle Tx,x\rangle \,,\quad M=\sup _{\|x\|=1}\langle Tx,x\rangle \,.}$

Ayrıca, m ve M'nin her ikisi de aslında spektrum içinde bulunur.

T operatörünün özuzayları şu şekilde verilir:

${\displaystyle H_{\lambda }=\ker(T-\lambda )\,.}$

Sonlu matrislerden farklı olarak, T spektrumunun her elemanı bir özdeğer olmak zorunda değildir: lineer operatör T − λ , surjective olmadığı için sadece bir tersi olmayabilir. Genel anlamda bir operatörün spektrumunun elemanları spektral değerler olarak bilinir . Spektral değerlerin özdeğer olması gerekmediğinden, spektral ayrışma genellikle sonlu boyutlarda olduğundan daha incedir.

Bununla birlikte, T kendi kendine eşlenik operatörünün spektral teoremi , ek olarak, T'nin bir kompakt operatör olduğu varsayılırsa , özellikle basit bir biçim alır . Kompakt kendine eş operatörler için spektral teoremi devletler:

• Bir kompakt kendinden-eşlenik operatör T sadece sayılabilir (veya sonlu olarak) birçok spektral değere sahiptir. T spektrumunun karmaşık düzlemde muhtemelen sıfır dışında bir sınır noktası yoktur . T'nin özuzayları, H'yi dik bir doğrudan toplama ayrıştırır :
  $${\displaystyle H=\bigoplus _{\lambda \in \sigma (T)}H_{\lambda }\,.}$$

  
  Ayrıca, eğer E _λ özuzay H _λ üzerindeki ortogonal izdüşümü gösteriyorsa , o zaman
  $${\displaystyle T=\sum _{\lambda \in \sigma (T)}\lambda E_{\lambda }\,,}$$

  
  burada toplam B( H ) üzerindeki norma göre yakınsar .

Bu teorem, integral denklemler teorisinde temel bir rol oynar , çünkü birçok integral operatör, özellikle Hilbert-Schmidt operatörlerinden ortaya çıkanlar kompakttır .

Kendine-eşleşen operatörler için genel spektral teorem , sonsuz bir toplamdan ziyade bir tür operatör değerli Riemann-Stieltjes integralini içerir . Spektral ailesi ile ilişkili T , bir operatörün λ her bir gerçek sayısı ortakları E _X operatörün nullspace üzerine projeksiyonu, ( T - λ ) ⁺ , bir kendi kendine eşlenik operatörün olumlu bir parçası ile tanımlanmaktadır

${\displaystyle A^{+}={\tfrac {1}{2}}\left({\sqrt {A^{2}}}+A\sağ)\,.}$

E _λ operatörleri , kendine eşlenik operatörlerde tanımlanan kısmi sıraya göre monoton artandır; özdeğerler tam olarak atlama süreksizliklerine karşılık gelir. Bir spektral teorem var, ki bu

${\displaystyle T=\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{\lambda }\,.}$

İntegral, B( H ) üzerindeki norma göre yakınsak bir Riemann-Stieltjes integrali olarak anlaşılır . Özellikle, sıradan skaler değerli integral gösterimi

${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} \langle E_{\lambda }x,y\rangle \,.}$

Benzer bir spektral ayrıştırma normal operatörler için geçerlidir, ancak spektrum artık gerçek olmayan karmaşık sayılar içerebileceğinden, operatör değerli Stieltjes ölçüsü d E _λ bunun yerine kimliğin bir çözünürlüğü ile değiştirilmelidir .

Spektral yöntemlerin önemli bir uygulamasıdır spektral dönüşüm teoremi biri özeslenik'tir uygulamak sağlar, T herhangi bir sürekli karmaşık fonksiyonu f spektrumu tanımlanan T entegrali oluşturarak

${\displaystyle f(T)=\int _{\sigma (T)}f(\lambda )\,\mathrm {d} E_{\lambda }\,.}$

Ortaya çıkan sürekli fonksiyonel hesap , özellikle psödodiferansiyel operatörler için uygulamalara sahiptir .

Sınırsız kendine eşlenik operatörlerin spektral teorisi, sınırlı operatörlerden yalnızca marjinal olarak daha zordur. Sınırsız bir operatörün spektrumu, tam olarak sınırlı operatörlerle aynı şekilde tanımlanır: λ , çözücü operatörü ise spektral bir değerdir.

${\displaystyle R_{\lambda }=(T-\lambda )^{-1}}$

iyi tanımlanmış bir sürekli operatör olamaz. T'nin kendi kendine bitişikliği hala spektrumun gerçek olduğunu garanti eder. Böylece sınırsız operatörler ile çalışmanın temel fikri resolvent de yerine bakmaktır R _X λ ötesi olduğunu. Bu, daha sonra T'nin kendisinin bir spektral temsiline aktarılabilen bir spektral gösterimi kabul eden bir sınırlı normal operatördür . Örneğin, Laplace operatörünün spektrumunu incelemek için benzer bir strateji kullanılır: operatöre doğrudan hitap etmek yerine, bunun yerine Riesz potansiyeli veya Bessel potansiyeli gibi ilişkili bir çözücü olarak görünür .

Bu durumda spektral teoremin kesin bir versiyonu şudur:

Bir Hilbert uzayı H üzerinde yoğun olarak tanımlanmış bir kendine-eşlenik operatör T verildiğinde, R'nin Borel kümelerinde E kimliğinin benzersiz bir çözünürlüğüne karşılık gelir , öyle ki

${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{x,y}(\lambda )}$

tüm x ∈ D ( T ) ve y ∈ H için . Spektral ölçü E , T'nin spektrumu üzerinde yoğunlaşmıştır .

Sınırsız normal operatörler için geçerli olan spektral teoremin bir versiyonu da vardır.

popüler kültürde

Thomas Pynchon , 1973 tarihli Gravity's Rainbow adlı romanında kurgusal karakter Sammy Hilbert-Spaess'i ("Hilbert Space" konulu bir kelime oyunu) tanıttı . Hilbert-Spaess önce "her yerde bulunan bir ikili ajan" ve daha sonra "en az bir ikili ajan" olarak tanımlandı. Roman önceki dost Alman matematikçi çalışmalarını başvurulan etmişti Kurt Gödel 'in Eksiklik Teoremleri gösterdi, Hilbert'in Programı , aksiyomların tek bir set haline Birleştir'me matematik Hilbert'in resmiyete plan mümkün değildi.

Ayrıca bakınız

Uyarılar

Notlar

Referanslar

Dış bağlantılar

• "Hilbert uzayı" , Matematik Ansiklopedisi , EMS Press , 2001 [1994]
• Mathworld'de Hilbert uzayı
• 245B, not 5: Terence Tao tarafından Hilbert uzayları