Euler diyagramı -Euler diagram

"Dört ayaklı hayvanlar" kümesinin "hayvanlar"ın bir alt kümesi olduğunu, ancak "mineraller" kümesinin "hayvanlar" ile ayrık olduğunu (ortak hiçbir üyesi olmadığını) gösteren bir Euler diyagramı

Farklı Güneş Sistemi nesneleri arasındaki ilişkileri gösteren bir Euler diyagramı

Bir Euler diyagramı ( / ˈ l ər / , OY -lər ), kümeleri ve onların ilişkilerini temsil etmenin diyagramatik bir yoludur. Karmaşık hiyerarşileri ve örtüşen tanımları açıklamak için özellikle yararlıdırlar. Başka bir küme diyagramlama tekniği olan Venn diyagramlarına benzerler . Farklı kümeler arasındaki tüm olası ilişkileri gösteren Venn diyagramlarından farklı olarak, Euler diyagramı yalnızca ilgili ilişkileri gösterir.

"Eulerian çemberleri"nin ilk kullanımı genellikle İsviçreli matematikçi Leonhard Euler'e (1707-1783) atfedilir. Amerika Birleşik Devletleri'nde, hem Venn hem de Euler diyagramları , 1960'ların yeni matematik hareketinin bir parçası olarak küme teorisindeki talimatın bir parçası olarak dahil edildi. O zamandan beri, okuma gibi diğer müfredat alanlarının yanı sıra kuruluşlar ve işletmeler tarafından da benimsenmiştir.

Euler diyagramları, her biri bir küme veya kategoriyi gösteren iki boyutlu bir düzlemde basit kapalı şekillerden oluşur. Bu şekillerin nasıl örtüştüğü veya örtüşmediği, kümeler arasındaki ilişkileri gösterir. Her eğri, düzlemi iki bölgeye veya "bölgeye" böler: kümenin öğelerini sembolik olarak temsil eden iç kısım ve kümenin üyesi olmayan tüm öğeleri temsil eden dış kısım. Üst üste binmeyen eğriler, ortak hiçbir öğesi olmayan ayrık kümeleri temsil eder. Üst üste binen iki eğri , ortak öğeleri olan kesişen kümeleri temsil eder ; her iki eğrinin içindeki bölge, her iki kümede ortak olan öğeler kümesini temsil eder (kümelerin kesişimi ). Tamamen bir başkasının içinde olan bir eğri, onun bir alt kümesidir .

Venn diyagramları , Euler diyagramlarının daha kısıtlayıcı bir şeklidir. Bir Venn diyagramı, n eğrisi arasında mantıksal olarak olası 2 ⁿ örtüşme bölgesinin tamamını içermelidir ve bu, bileşen kümelerinin tüm dahil edilmesi/hariç tutulması kombinasyonlarını temsil eder. Kümenin parçası olmayan bölgeler, küme üyeliğinin renk kadar örtüşme ile gösterildiği Euler diyagramlarının aksine, siyah renkle gösterilir.

Tarih

Hamilton'un Mantık Üzerine Derslerinden bir sayfa . A, E, I ve O sembolizmi, bir kıyasta meydana gelebilecek kategorik ifadeleri ifade eder . Soldaki küçük metin hatalı bir şekilde şöyle diyor: "Mantıkta dairesel diyagramların ilk kullanımı uygunsuz bir şekilde Euler'e atfedildi. Christian Weise'de bulunacak", aslında Johann Christian Lange tarafından yazılmış bir kitap.

Sağda, Couturat 1914'ün 74. sayfasında, Venn diyagramının 8 bölgesini etiketliyor. Bu "bölgeler"in modern adı minterms'dir . Bunlar, Venn'in çizimine göre x, y ve z değişkenleri ile solda gösterilmektedir. Sembolizm aşağıdaki gibidir: mantıksal AND ( & ) aritmetik çarpma ile temsil edilir ve mantıksal NOT ( ~ ) değişkenden sonra " ' " ile temsil edilir, örneğin x'y'z bölgesi "NOT x AND NOT olarak okunur y VE z" yani ~x & ~y & z.

Hem Veitch diyagramı hem de Karnaugh haritası tüm mintermleri gösterir , ancak Veitch formüllerin indirgenmesi için özellikle kullanışlı değildir. Venn ve Karnaugh diyagramları arasındaki güçlü benzerliğe dikkat edin; renkler ve x, y ve z değişkenleri Venn örneğine göredir.

Sağdaki resimde gösterildiği gibi, Sir William Hamilton , ölümünden sonra yayınlanan Lectures on Metaphysics and Logic (1858–60) adlı eserinde, hatalı bir şekilde, çemberlerin orijinal kullanımının "Mantığın soyutlamalarını... Leonhard Paul Euler (1707-1783) değil , ölümünden sonra 1712'de çıkan Nucleus Logicae Weisianae'deki Christian Weise (1642-1708) idi , ancak ikinci kitap aslında Weise yerine Johann Christian Lange tarafından yazılmıştır. Euler'in Alman Prensesine Mektupları'na atıfta bulunuyor [Partie II, Lettre XXXV, 17 Şubat 1791, ed. Cournot (1842), s. 412–417. – ED.]

Hamilton'un çiziminde, A, E, I ve O çizimleriyle sembolize edilen bir kıyasta meydana gelebilecek dört kategorik önerme şunlardır:

• C: Evrensel Olumlu , Örnek: "Bütün metaller elementtir".
• E: Evrensel Negatif , Örnek: "Hiçbir metal bileşik madde değildir".
• I: Özel Olumlu , Örnek: "Bazı metaller kırılgandır".
• O: Özel Negatif , Örnek: "Bazı metaller kırılgan değildir".

John Venn (1834–1923) , 1881 Sembolik Mantık Bölüm V "Diyagramatik Temsil" adlı eserinde Euler diyagramının dikkate değer yaygınlığı hakkında şu yorumu yapar:

"...geçen yüzyılda yayınlanan ve bu amaçla başvurulan ilk altmış mantıksal incelemeden: -en erişilebilir oldukları için biraz rastgele:- diyagramlar, bunların neredeyse tamamı Euler Şemasını kullanıyor." (Dipnot 1 sayfa 100)

Venn 1881'den iki sayfa 115-116'dan oluşan bileşik, üç parçadan oluşan bir kıyasın kendi diyagram tipine nasıl dönüştürüleceğine dair örneğini gösteriyor. Venn, "eski moda Euler diyagramları"nın (Venn 1881:113) "Eulerian şemasında" (Venn 1881:100) dairelere "Eulerian daireleri" (cf Sandifer 2003, Venn 1881:114 vb.) adını verir.

Ancak yine de, "bu şemanın gerçekten genel bir Mantığın amaçları için uygulanamaz olduğunu" iddia etti (sayfa 100) ve 101. sayfada şunu gözlemledi: normal olarak uygulanır." Venn, bölümünü aşağıdaki örneklerde gösterilen gözlemle bitiriyor—bunların kullanımının katı bir algoritmik uygulamaya değil, uygulamaya ve sezgiye dayandığı :

"Aslında... bu diyagramlar, örneklemek için kullanıldıkları sıradan önermeler şemasına uymamakla kalmaz, aynı zamanda tutarlı bir şekilde bağlanabilecekleri bilinen herhangi bir önerme şemasına da sahip değil gibi görünürler." (s. 124–125)

Son olarak, Bölüm XX TARİHİ NOTLAR'da Venn çok önemli bir eleştiriye ulaşır (aşağıdaki alıntıda italik yazılmıştır); Hamilton'un çiziminde O ( Özel Negatif ) ve I'in ( Özel Olumlu ) basitçe döndürüldüğünü gözlemleyin:

"Şimdi, Euler'in ilk olarak Lettres a une Princesse d'Allemagne (Mektup 102–105) adlı eserinde tanımlanan iyi bilinen çevrelerine geliyoruz. Bunlarla ilgili zayıf nokta, yalnızca sınıfların gerçek ilişkilerini kesin olarak göstermeleridir. önerme aracılığıyla sahip olabileceğimiz ya da iletmek isteyebileceğimiz bu ilişkilerin eksik bilgisinden ziyade, birbirlerine karşıdırlar. uygun temel önermeler.... Bu kusur, belirli olumlu ve olumsuz durumunda daha baştan fark edilmiş olmalıdır , çünkü aynı diyagram, her ikisini de temsil etmek için yaygın olarak kullanılır ve kayıtsızca iyi yapar ". (italik eklendi: sayfa 424)

(Sandifer 2003, Euler'in de bu tür gözlemler yaptığını bildirir; Euler, 45 rakamının (iki dairenin basit bir kesişimi) 4 farklı yorumu olduğunu bildirir). Durum ne olursa olsun, bu gözlemler ve eleştirilerle donanmış olan Venn daha sonra (s. 100–125) kendi Venn diyagramları olarak bilinen şeyi "...eski moda Euler diyagramlarından" nasıl çıkardığını gösterir. Özellikle solda gösterilen bir örnek veriyor.

1914'te Louis Couturat (1868–1914), terimleri sağdaki çizimde gösterildiği gibi etiketlemişti. Ayrıca (a'b'c' olarak gösterilen) dış bölgeyi de etiketlemişti. Diyagramın nasıl kullanılacağını kısa ve öz bir şekilde açıklıyor – kaybolacak bölgelerin üzeri çizilmelidir:

"VENN'in yöntemi, tüm bileşenleri temsil eden geometrik diyagramlara çevrilir, bu nedenle, sonucu elde etmek için, sadece problemin verileri tarafından yok edilenlerin üzerini çizmemiz (gölgelendirme yoluyla) gerekir." (italikler eklendi s. 73)

Venn'in atamaları göz önüne alındığında, dairelerin içindeki gölgelenmemiş alanlar Venn örneği için aşağıdaki denklemi verecek şekilde toplanabilir:

"Hayır Y Z'dir ve TÜM X Y'dir: bu nedenle Hiçbir X Z'dir", dairelerin içindeki gölgelenmemiş alan için x'yz' + xyz' + x'y'z denklemine sahiptir (ancak bu tamamen doğru değildir; bkz. sonraki paragraf).

Venn'de 0. terim olan x'y'z' yani daireleri çevreleyen arka plan görünmez. Hiçbir yerde tartışılmıyor veya etiketlenmiyor, ancak Couturat bunu çiziminde düzeltiyor. Doğru denklem, kalın harflerle gösterilen bu gölgelenmemiş alanı içermelidir:

"Hayır Y Z'dir ve TÜM X Y'dir: bu nedenle Hiçbir X Z değildir", x'yz' + xyz' + x'y'z + x'y'z' denklemine sahiptir .

Modern kullanımda, Venn şeması tüm daireleri çevreleyen bir "kutu" içerir; buna söylem evreni veya söylem alanı denir .

Couturat şimdi, doğrudan algoritmik (biçimsel, sistematik) bir şekilde, indirgenmiş Boole denklemlerinin türetilemediğini ve "Hiçbir X, Z değildir" sonucuna nasıl ulaşılacağını göstermediğini gözlemliyor. Couturat, sürecin "mantıksal sorunları çözmek için bir yöntem olarak ciddi sakıncaları olduğu" sonucuna varmıştır:

"Belirli bileşenlerin iptal edilmesiyle verilerin nasıl sergilendiğini göstermez, kalan bileşenlerin nasıl birleştirileceğini de göstermez, böylece aranan sonuçları elde eder. Kısacası, argümanda yalnızca tek bir adım sergilemeye hizmet eder, yani problemin denklemi; ne önceki adımlardan, yani "problemin bir denkleme dönüştürülmesi" ve öncüllerin dönüştürülmesinden ne de sonraki adımlardan, yani çeşitli sonuçlara yol açan kombinasyonlardan vazgeçer. bileşenleri düzlem bölgeler kadar cebirsel sembollerle temsil edilebildiği ve bu formda ele alınması çok daha kolay olduğu için çok az kullanışlıdır."(s. 75)

Böylece mesele, Maurice Karnaugh'un (1924– ) Edward W. Veitch tarafından önerilen bir yöntemi uyarlayıp genişleteceği 1952 yılına kadar duracaktı ; bu çalışma, Emil Post'un 1921 tarihli "Temel önermelerin genel bir teorisine giriş" adlı doktora tezinde tam olarak tanımlanan doğruluk tablosu yöntemine ve (diğerlerinin yanı sıra) Claude Shannon , George Stibitz ve Alan Turing'in fotoğrafı . Örneğin, "Boole Cebiri" bölümünde, Hill ve Peterson (1968, 1964) 4.5ff "Boole Cebirinin Örneği Olarak Küme Teorisi" bölümlerini sunarlar ve bu bölümde gölgelendirme ve tüm Venn diyagramını sunarlar. Örnek anahtarlama devresi problemlerini çözmek için Venn diyagramlarından örnekler verirler, ancak şu ifadeyle sonuçlanırlar:

"Üçten fazla değişken için, Venn diyagramının temel açıklayıcı biçimi yetersizdir. Ancak, en uygunu Bölüm 6'da tartışılacak olan Karnaugh haritası olan uzantılar mümkündür." (s. 64)

Bölüm 6, bölüm 6.4 "Boolean Fonksiyonlarının Karnaugh Harita Temsili" bölümünde şu şekilde başlarlar:

"Karnaugh haritası ¹ [ ¹ Karnaugh 1953], mantık tasarımcısının repertuarındaki en güçlü araçlardan biridir. ... Bir Karnaugh haritası, bir doğruluk tablosunun resimli bir biçimi veya Venn'in bir uzantısı olarak kabul edilebilir. diyagram." (s. 103-104)

Karnaugh'un "harita" veya "harita" yöntemini geliştirmesinin tarihi belirsizdir. Karnaugh 1953'te Veitch 1951'e atıfta bulundu, Veitch Claude E. Shannon 1938'e atıfta bulundu (esas olarak Shannon'ın MIT'deki yüksek lisans tezi ) ve Shannon da diğer mantık metinleri yazarları arasında Couturat 1914'e atıfta bulundu. Veitch'in yönteminde değişkenler bir dikdörtgen içinde düzenlenmiştir. veya kare; Karnaugh haritasında açıklandığı gibi , Karnaugh yönteminde değişkenlerin sırasını hiperküp (köşeleri) olarak bilinen şeye karşılık gelecek şekilde değiştirdi .

Euler ve Venn diyagramları arasındaki ilişki

Boş kümeleri temsil eden gölgeli bölgelere sahip küçük Venn diyagramlarının örnekleri (solda) , eşdeğer Euler diyagramlarına nasıl kolayca dönüştürülebileceklerini gösteren (sağda)

Venn diyagramları , Euler diyagramlarının daha kısıtlayıcı bir şeklidir. Bir Venn diyagramı, n eğrisi arasında mantıksal olarak olası 2 ⁿ örtüşme bölgesinin tamamını içermelidir ve bu, bileşen kümelerinin tüm dahil edilmesi/hariç tutulması kombinasyonlarını temsil eder. Kümenin parçası olmayan bölgeler, küme üyeliğinin renk kadar örtüşme ile gösterildiği Euler diyagramlarının aksine, siyah renkle gösterilir. Küme sayısı 3'ün üzerine çıktığında, bir Venn diyagramı, özellikle karşılık gelen Euler diyagramıyla karşılaştırıldığında, görsel olarak karmaşık hale gelir. Euler ve Venn diyagramları arasındaki fark aşağıdaki örnekte görülebilir. Üç seti alın:

• ${\ Displaystyle A=\{1,\,2,\,5\}}$
• ${\ Displaystyle B=\{1,\,6\}}$
• ${\ Displaystyle C=\{4,\,7\}}$

Bu kümelerin Euler ve Venn diyagramları:

• 

  Euler diyagramı

• 

  Venn şeması

Mantıksal bir ortamda, bir söylem evreni içinde Euler diyagramlarını yorumlamak için model-teorik anlambilim kullanılabilir . Aşağıdaki örneklerde, Euler diyagramı, karşılık gelen eğriler ayrık olduğundan Animal ve Mineral kümelerinin ayrık olduğunu ve ayrıca Four Legs kümesinin Animal s kümesinin bir alt kümesi olduğunu gösterir. Aynı Animal , Mineral ve Four Legs kategorilerini kullanan Venn diyagramı bu ilişkileri kapsamaz. Geleneksel olarak Venn diyagramlarında bir kümenin boşluğu , bölgedeki gölgeleme ile gösterilir. Euler diyagramları, boşluğu gölgelendirme veya bir bölgenin yokluğu ile temsil eder.

Genellikle bir dizi iyi biçimlenme koşulu uygulanır; bunlar, diyagramın yapısına dayatılan topolojik veya geometrik kısıtlamalardır. Örneğin, bölgelerin bağlantılılığı zorunlu kılınabilir veya eğrilerin veya birden çok noktanın eşzamanlılığı yasaklanabilir ve eğrilerin teğetsel kesişimi yasaklanabilir. Bitişik diyagramda, küçük Venn diyagramlarının örnekleri, dönüşüm dizileriyle Euler diyagramlarına dönüştürülür; ara diyagramlardan bazıları eğrilerin eşzamanlılığına sahiptir. Bununla birlikte, gölgelemeli bir Venn diyagramının gölgelemesiz bir Euler diyagramına dönüştürülmesi her zaman mümkün değildir. Düzlemsel olmayan ikili grafiklere sahip olmaları gerektiğinden, istenmeyen bölgeler oluşturulmadan basit kapalı eğriler kullanılarak çizilemeyen 9 kümeli Euler diyagramlarının örnekleri vardır.

Örnek: Euler'den Venn'e diyagramı ve Karnaugh haritası

Bu örnek, Euler ve Venn diyagramlarını ve Karnaugh haritasını "Hiçbir X s, Z s değildir" çıkarımını türeten ve doğrulayan gösterir. Çizimde ve tabloda aşağıdaki mantıksal semboller kullanılmıştır:

• 1 "doğru", 0 "yanlış" olarak okunabilir
• ~ NOT için ve mintermleri gösterirken ' olarak kısaltılır, örneğin x' = _tanımlı NOT x,
• + Boole VEYA için ( Boole cebirinden : 0 + 0 = 0, 0 + 1 = 1 + 0 = 1, 1 + 1 = 1)
• & (mantıksal VE) önermeler arasında; mintermlerde AND, aritmetik çarpmaya benzer bir şekilde atlanır: örneğin x'y'z = _{tanımlanmış} ~x & ~y & z (Boole cebirinden: 0·0 = 0, 0·1 = 1·0 = 0, 1·1 = 1, burada "·" netlik için gösterilmiştir)
• → (mantıksal UYGULAMA): IF ... THEN ... veya " IMPLIES " olarak okuyun, P → Q =  _tanımlı NOT P OR Q

Bir Venn diyagramında veya Karnaugh Haritasında sunulmadan önce, Euler diyagramının "Hayır Y , Z'dir , Tüm X Y'dir " kıyasının, ilk önce önermeler hesabının daha resmi dilinde yeniden yazılması gerekir : " 'Öyle değil. : Y VE Z' VE 'Eğer bir X ise bir Y' ". Önermeler sembollere ve bir önerme formülüne ( ~(y & z) & (x → y) ) indirgendiğinde, formülün doğruluk tablosu oluşturulabilir ; bu tablodan Venn ve/veya Karnaugh haritası kolayca üretilir. Karnaugh haritasındaki "1"lerin bitişikliğini kullanarak (0 ve 1 terimleri ve 2 ve 6 terimlerinin etrafındaki gri ovallerle gösterilir) örneğin Boole denklemi "azaltılabilir" yani (x'y'z' + x'y'z) + (x'yz' + xyz') sadece iki terime çevirir: x'y' + yz'. Ancak, "X'in Z olmadığı" fikrini çıkarmanın yolu ve indirgemenin bu çıkarımla nasıl ilişkili olduğu bu örnekten öğrenilemez.

"No X , Z'dir " gibi önerilen bir sonuç göz önüne alındığında , bir doğruluk tablosu kullanılarak bunun doğru bir çıkarım olup olmadığı test edilebilir . En kolay yöntem, başlangıç ​​formülünü sola koymak (kısaltmak P ) ve (olası) kesintiyi sağa koymak ( Q olarak kısaltın ) ve ikisini mantıksal çıkarımla bağlamak, yani P → Q , IF P THEN olarak okuyun S. _ Doğruluk tablosunun değerlendirmesi, ima-işareti (→, ana bağlaç olarak adlandırılan ) altında tüm 1'leri üretiyorsa, o zaman P → Q bir totolojidir . Bu gerçek göz önüne alındığında, sağdaki formül ( Q olarak kısaltılır ) doğruluk tablosunun altında açıklanan şekilde "ayırılabilir".

Yukarıdaki örnekte, Euler ve Venn diyagramlarının formülü şu şekildedir:

" Y'lerin hiçbiri Z'dir " ve "Tüm X'ler Y'dir " : ( ~(y & z) & (x → y) ) = _{tanımlanmış} P

Ve önerilen kesinti:

" X s, Z s değildir": ( ~ (x & z) ) = _{tanımlanmış} Q

Şimdi değerlendirilecek formül şu şekilde kısaltılabilir:

( ~(y & z) & (x → y) ) → ( ~ (x & z) ): P → Q

EĞER ("Hayır Y'ler Z'dir " ve "Tüm X'ler Y'dir ") THEN ( " Hiçbir X , Z'dir " )

Bu noktada, yukarıdaki P → Q (yani ~(y & z) & (x → y) ) → ~(x & z) ) hala bir formüldür ve tümdengelim – Q'nun P'den " ayrılması" → Q – oluşmadı. Ancak, P → Q'nun totoloji olduğunun ispatı göz önüne alındığında, şimdi modus ponens prosedürünün kullanımı için aşama, Q'yu "ayırmak" için hazırlanmıştır: "Hiçbir X , Z değildir " ve soldaki terimlerden vazgeçer.

Modus ponens (veya "temel çıkarım kuralı") genellikle şu şekilde yazılır: Soldaki iki terim olan P → Q ve P , öncül olarak adlandırılır (geleneksel olarak virgülle birbirine bağlanır), ⊢ sembolü "verimler" anlamına gelir. (mantıksal tümdengelim anlamında) ve sağdaki terime sonuç denir :

P → Q , P ⊢ Q

Modus ponens'in başarılı olması için, hem P → Q hem de P öncüllerinin doğru olması gerekir . Yukarıda gösterildiği gibi, P → Q öncülü bir totoloji olduğundan, x, y ve z'nin değeri ne olursa olsun "hakikat" her zaman geçerlidir, ancak "hakikat" yalnızca P için geçerlidir, ancak P " olarak değerlendirildiğinde bu koşullarda "gerçek". true" (ör. satır 0 VEYA 1 VEYA 2 VEYA 6 : x'y'z' + x'y'z + x'yz' + xyz' = x'y' + yz').

P → Q , P ⊢ Q

• yani: ( ~(y & z) & (x → y) ) → ( ~ (x & z) ) , ( ~(y & z) & (x → y) ) ⊢ ( ~ (x & z) )
• yani: EĞER "Hayır Y'ler Z'dir " ve " Tüm X'ler Y'dir " SONRA " Hayır X'ler Z'dir " , " Hayır Y'ler Z'dir " ve "Tüm X'ler Y'dir " ⊢ " Hayır X'ler Z'dir " _

Kişi artık "Hiçbir X , Z değildir " sonucunu "ayırmakta" , belki de onu sonraki bir çıkarımda (veya bir konuşma konusu olarak) kullanmakta özgürdür.

Totolojik çıkarımın kullanılması, "Hiçbir X s, Z s değildir" dışında başka olası tümdengelimlerin de var olduğu anlamına gelir ; Başarılı bir çıkarım için kriter, sağdaki alt ana bağlaç altındaki 1'lerin, soldaki alt ana bağlaç altındaki tüm 1'leri içermesidir ( ana bağlaç, totolojiyle sonuçlanan imadır). Örneğin, doğruluk tablosunda, çıkarımın sağ tarafında (→, ana bağlaç sembolü) alt ana bağlaç sembolü " ~ " altındaki kalın sütun, kalın harflerle gösterilen tüm aynı 1'lere sahiptir. sol taraftaki alt ana bağlacı & (sıra 0 , 1 , 2 ve 6 ) altındaki yüzlü sütun, artı iki tane daha (sıra 3 ve 4 ).

Galeri

Çeşitli çok uluslu Avrupa kuruluşları ve anlaşmaları arasındaki ilişkileri gösteren tıklanabilir bir Euler diyagramı ^{[dosyası] .}

• v
• t
• e

• 

  Bir Venn şeması tüm olası kesişmeleri gösterir.

• 

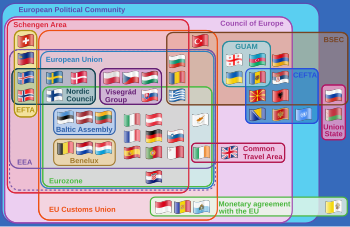
  Gerçek bir durumu, çeşitli uluslarüstü Avrupa örgütleri arasındaki ilişkileri görselleştiren Euler diyagramı . ( tıklanabilir sürüm )

• 

  Euler ve Venn diyagramlarını karşılaştıran mizahi diyagram .

• 

  Euler üçgen türleri diyagramı, ikizkenar üçgenlerin en az (tam olarak değil) 2 eşit kenara sahip olduğu tanımını kullanarak.

• 

  Britanya Adaları terminolojisinin Euler diyagramı .

• 

  3 daire (üstte) ve bunlara karşılık gelen Euler diyagramları (altta) ile 22 (256) esasen farklı Venn diyagramları
  Euler diyagramlarından bazıları tipik değildir ve hatta bazıları Venn diyagramlarına eşdeğerdir. Alanlar, hiçbir öğe içermediklerini belirtmek için gölgelenir.

• 

  Henri Milne -Edwards'ın (1844) omurgalı hayvanların ilişkileri diyagramı, bir dizi iç içe küme olarak gösterilmiştir.

Ayrıca bakınız

• Gökkuşağı kutusu
• Örümcek diyagramı – kontur kesişimlerine varlık ekleyen Euler diyagramlarının bir uzantısı.
• Venn şeması

Notlar

Referanslar

daha fazla okuma

Yayınlanma tarihine göre:

• Sir William Hamilton 1860 Metafizik ve Mantık Üzerine Dersler, Henry Longueville Mansel ve John Veitch , William Blackwood ve Sons , Edinburgh ve Londra tarafından düzenlendi .
• W. Stanley Jevons 1880 Temel Mantık Dersleri: Tümdengelim ve Tümevarım. Bol Sorular ve Örnekler ve Mantıksal Terimler Sözlüğü ile MA MacMillan and Co. , London and New York.
• Alfred North Whitehead ve Bertrand Russell 1913 1. baskı, 1927 2. baskı Principia Mathematica'dan *56 Cambridge At The University Press (1962 baskısı), Birleşik Krallık, ISBN yok.
• Louis Couturat 1914 Mantığın Cebiri: Philip EB Jourdain , The Open Court Publishing Company , Chicago ve Londra'nın Önsözüyle Lydia Gillingham Robinson tarafından Yetkili İngilizce Çevirisi .
• Emil Post 1921 "Temel önermelerin genel bir teorisine giriş" Jean van Heijenoort'un yorumlarıyla yeniden basıldı Jean van Heijenoort, editör 1967 Frege'den Gödel'e : Matematiksel Mantığın Kaynak Kitabı, 1879–1931 , Harvard University Press , Cambridge, MA , ISBN  0-674-32449-8 (pbk.)
• Claude E. Shannon 1938 "Röle ve Anahtarlama Devrelerinin Sembolik Bir Analizi", İşlemler Amerikan Elektrik Mühendisleri Enstitüsü cilt 57, s. 471-495. Claude Elwood Shannon'dan türetilmiştir : NJA Solane ve Aaron D. Wyner, IEEE Press , New York tarafından düzenlenen Collected Papers.
• Hans Reichenbach 1947 Elements of Symbolic Logic , 1980'de Dover Publications, Inc. , NY, ISBN  0-486-24004-5 tarafından yeniden yayınlandı .
• Veitch, Edward Westbrook (1952-05-03) [1952-05-02]. "Hakikat İşlevlerini Basitleştirmek İçin Bir Grafik Yöntemi". 1952 ACM Yıllık Toplantısının İşlemleri . ACM Yıllık Konferansı/Yıllık Toplantısı: 1952 ACM Yıllık Toplantısının Tutanakları (Pittsburgh, Pennsylvania, ABD). New York, ABD: Bilgisayar Makineleri Birliği (ACM): 127-133. doi : 10.1145/609784.609801 . S2CID  17284651 .
• Karnaugh, Maurice (Kasım 1953) [1953-04-23, 1953-03-17]. "Birleşimsel Mantık Devrelerinin Sentezi için Harita Yöntemi" (PDF) . Amerikan Elektrik Mühendisleri Enstitüsü'nün İşlemleri, Bölüm I: İletişim ve Elektronik . 72 (5): 593–599. doi : 10.1109/TCE.1953.6371932 . S2CID  51636736 . Kağıt 53-217. Orijinalinden (PDF) 2017-04-16 tarihinde arşivlendi . 2017-04-16 alındı .
• Frederich J. Hill ve Gerald R. Peterson 1968, 1974 Anahtarlama Teorisine ve Mantıksal Tasarıma Giriş , John Wiley & Sons , NY, ISBN  978-0-471-39882-0 .
• Sandifer, Ed (Ocak 2004). "Euler Bunu Nasıl Yaptı" (PDF) . maa.org . Orijinalinden (PDF) 2013-01-26 tarihinde arşivlendi .

Dış bağlantılar

• Euler Diyagramları. Brighton, Birleşik Krallık (2004). Euler diyagramları nedir?