Meşgul kunduz - Busy beaver
Gelen teorik bilgisayar bilimleri , yoğun kunduz oyunu bir sonlandırma bulma amacı programı mümkün olan en çıktı üretir belirli bir boyutta. Bir yana hiç durmadan döngü sonsuz çıktı üreten bir program kolayca tasavvur edilir, bu tür programlar oyun dışında bırakılır.
Daha doğrusu, meşgul kunduz oyunu , yalnızca belirli bir dizi durumu kullanarak, bant üzerine en fazla 1'i yazan, durdurmalı, ikili alfabeli bir Turing makinesi tasarlamaktan ibarettir . 2 devletli oyunun kuralları aşağıdaki gibidir:
- makinenin durma durumuna ek olarak iki durumu olmalıdır ve
- bant başlangıçta yalnızca 0'lar içerir.
Bir oyuncu, makinenin sonunda duracağından emin olarak, bantta en uzun 1 saniyelik çıktıyı hedefleyen bir geçiş tablosu tasarlamalıdır.
Bir n inci meşgul kunduz , BB- n veya basitçe "meşgul kunduz" kazanır Turing makinesi n -devlet Meşgul Beaver Oyunu. Yani, diğer tüm olası n- durumlu rakip Turing Makineleri arasında en fazla 1 sayısına ulaşır . BB-2 Turing makinesi , örneğin, altı adımda dört 1s elde edilir.
Rastgele bir Turing makinesinin meşgul bir kunduz olup olmadığını belirlemek karar verilemez . Bunun hesaplanabilirlik teorisinde , durma probleminde ve karmaşıklık teorisinde etkileri vardır . Konsept ilk olarak Tibor Radó tarafından 1962 tarihli "Hesaplanınamayan Fonksiyonlar Üzerine" makalesinde tanıtıldı .
Oyun
N -devlet meşgul kunduz oyunu (veya BB- n oyun ), tanıtıldı Tibor Radó 'ın 1962 kağıt, sınıfını içerir Turing makineleri aşağıdaki tasarım özellikleri karşılamak için gerekli olan her üye olan,:
- Makinenin n "operasyonel" durumu artı bir Halt durumu vardır, burada n pozitif bir tam sayıdır ve n durumundan biri başlangıç durumu olarak ayırt edilir. (Tipik olarak, durumlar 1, 2, ..., n , başlangıç durumu olarak durum 1 ile veya durum A başlangıç durumu olarak A , B , C , ... ile etiketlenir .)
- Makine, tek bir iki yönlü sonsuz (veya sınırsız) bant kullanır.
- Bant alfabesi {0, 1}'dir ve 0 boş sembol olarak işlev görür.
- Makinenin geçiş işlevi iki girdi alır:
- mevcut Durmayan durum,
- geçerli bant hücresindeki sembol,
- ve üç çıktı üretir:
- mevcut teyp hücresindeki sembolün üzerine yazılacak bir sembol (üzerine yazılan sembolle aynı sembol olabilir),
- hareket etmek için bir yön (sola veya sağa; yani, geçerli hücrenin solundaki veya sağındaki bir yerdeki teyp hücresine kaydırma) ve
- geçilecek bir durum (bu, Halt durumu olabilir).
- Bu nedenle (4 n + 4) 2 n n durumlu Turing makineleri bu tanımı karşılayan çünkü formülün genel formu ( semboller × yönler × ( durumlar + 1)) ( semboller × durumlar ) .
- Geçiş fonksiyonu, her biri formun her biri olan 5 demetin sonlu bir tablosu olarak görülebilir.
- (mevcut durum, mevcut sembol, yazılacak sembol, kaydırma yönü, sonraki durum).
Makineyi "çalıştırmak", mevcut bant hücresinin boş (tümü-0) bir bandın herhangi bir hücresi olduğu başlangıç durumunda başlatmayı ve ardından Durma durumuna girilene kadar (varsa) geçiş işlevini yinelemeyi içerir. Yalnızca ve ancak makine sonunda durursa, bantta kalan 1 saniyenin sayısına makinenin puanı denir .
N -devlet meşgul kunduz (BB- n ) oyunu böyle bir bulmak için bir yarışma n durdurulduğu sonra kasete 1'ler en fazla sayıda - mümkün olan en büyük skora sahip -devlet Turing makinesi. Tüm n- durumlu Turing makineleri arasında mümkün olan en yüksek puanı alan bir makineye n- durumlu meşgul kunduz denir ve puanı yalnızca şimdiye kadar elde edilen en yüksek (belki de mümkün olan en büyük olmayan) bir makineye şampiyon n- durumlu denir. makine.
Radó, yarışmaya katılan her makineye, Durdurma durumuna ulaşmak için atması gereken tam adım sayısının bir ifadesinin eşlik etmesini istedi, böylece makineyi belirtilen sayı için çalıştırarak her bir girişin puanının (prensipte) doğrulanmasına izin verdi. adımlardan oluşur. (Girişler yalnızca makine tanımlarından oluşacak olsaydı, o zaman her potansiyel girişi doğrulama sorununa karar verilemezdi, çünkü bu, iyi bilinen durma sorununa eşdeğerdir - keyfi bir makinenin sonunda durup durmayacağına karar vermenin etkili bir yolu olmazdı.)
İlgili işlevler
Meşgul kunduz işlevi Σ
Yoğun kunduz fonksiyonu belirli bir ölçü bir Meşgul Beaver maksimum skor elde edilebilen miktarını belirler. Bu hesaplanamaz bir fonksiyondur . Ayrıca, meşgul bir kunduz fonksiyonunun herhangi bir hesaplanabilir fonksiyondan asimptotik olarak daha hızlı büyüdüğü gösterilebilir .
Meşgul kunduz işlevi, Σ: ℕ → ℕ, Σ( n ) tüm durma 2 sembollü n durumlu Turing makineleri arasında elde edilebilecek maksimum puan (son olarak banttaki maksimum 1 sayısı) olacak şekilde tanımlanır. boş bir bantta başlatıldığında açıklanan tür.
Σ'nin iyi tanımlanmış bir fonksiyon olduğu açıktır: her n için , izomorfizme kadar en fazla sonlu sayıda n- durumlu Turing makinesi vardır , dolayısıyla en fazla sonlu sayıda olası çalışma süresi vardır.
Bu sonsuz bir dizi Σ olan yoğun kunduz fonksiyonu , herhangi bir n, -durum 2-simge Turing makinesi K olan σ ( M ) = Σ ( N (en yüksek puan ulaşır, yani,)) olarak da adlandırılır, yoğun bir kunduz . Her n için , en az dört n- durumlu meşgul kunduz bulunduğuna dikkat edin (çünkü, herhangi bir n- durumlu meşgul kunduz verildiğinde , bir diğeri sadece bir durma geçişinde kaydırma yönünü değiştirerek elde edilir, bir diğeri ise tüm yön değişikliklerini karşıtlarına kaydırarak elde edilir. , ve tamamen değiş tokuş edilen meşgul kunduzun durma yönünü değiştirerek son).
hesaplanamazlık
Rado 1962'de kağıt kanıtladı eğer f : ℕ → ℕ herhangi bir hesaplanabilir fonksiyon daha sonra, Σ ( n )> f (n) tüm yeterince büyük için n ve dolayısıyla Σ hesaplanabilir bir fonksiyon değildir.
Ayrıca, bu, keyfi bir Turing makinesinin meşgul bir kunduz olup olmadığına genel bir algoritma tarafından karar verilemeyeceğini ima eder . (Böyle bir algoritma var olamaz, çünkü varlığı Σ'nin hesaplanmasına izin verir ki bu kanıtlanmış bir imkânsızlıktır. Özellikle, böyle bir algoritma Σ'yi aşağıdaki gibi hesaplayacak başka bir algoritma oluşturmak için kullanılabilir: herhangi bir n için , her biri sonlu sayıda n durumlu 2 sembollü Turing makinesi, n durumlu bir meşgul kunduz bulunana kadar test edilecektir ; bu meşgul kunduz makinesi daha sonra, tanım gereği Σ( n ) olan puanını belirlemek için simüle edilecektir .)
Σ (olsa n ) bir uncomputable fonksiyonudur, bazı küçük vardır n onun değerlerini almak ve onlar doğru olduğunu kanıtlamak mümkün olduğu. Σ(0) = 0, Σ(1) = 1, Σ(2) = 4 olduğunu göstermek zor değildir ve giderek daha fazla zorlukla Σ(3) = 6 ve Σ(4) = olduğu gösterilebilir. 13 (dizi A028444 içinde OEIS ). Alt sınırlar belirlenmiş olmasına rağmen , n > 4'ün herhangi bir örneği için Σ( n ) henüz belirlenmemiştir ( aşağıdaki Bilinen değerler bölümüne bakın).
2016 yılında Adam Yedidia ve Scott Aaronson üst az üzerine bağlanmış (açık) bir elde edilen ilk n- S (kendisi için N ) 'de kanıtlanabilir değil ZFC . Onlar kimin davranış küme kuramı (olağan aksiyomlarından dayalı kanıtlanmış edilemez bir 7910-devlet Turing makinesi inşa Bunu yapmak için Zermelo-Fraenkel küme teorisinin ile seçim belitinin ), makul tutarlılık hipotez altında ( sabit Ramsey mülkiyet ). Bu daha sonra, sabit Ramsey mülküne olan bağımlılık ortadan kaldırılarak 1919 eyaletlerine ve daha sonra 748 eyalete düşürüldü.
Σ'nin karmaşıklığı ve kanıtlanamazlığı
Kolmogorov karmaşıklığının bir çeşidi aşağıdaki gibi tanımlanır [cf. Boolos, Burgess & Jeffrey, 2007]: karmaşıklığı Bir sayının n BB sınıf Turing makinesi için gerekli devletlerin küçük sayı olduğu bir tek bloklu durur n bir başlangıçta boş kasete ardışık 1'ler. Karşılık gelen varyant Chaitin olmayan teoremi belirli bir bağlamında, devletler aksiyomatik sistem doğal sayılar için, bir dizi vardır k belirli bir sayısı daha karmaşıklığı daha büyük olduğu kanıtlanmıştır şekildedir k ve bundan dolayı herhangi bir belirli üst bağlandığını S (için ispat edilebilir k ) (ikincisi "karmaşıklığı nedeni n daha büyüktür k " ise kanıtladı olacağını " n > Σ ( k )" ispat edilmiştir). Alıntılanan referansta belirtildiği gibi, "sıradan matematik"in herhangi bir aksiyomatik sistemi için bunun doğru olduğu en küçük k değeri 10↑↑10'dan çok daha küçüktür ; sonuç olarak, sıradan matematik bağlamında, Σ(10 ↑↑ 10)'un ne değeri ne de herhangi bir üst sınırı kanıtlanamaz. ( Gödel'in ilk eksiklik teoremi bu sonuçla gösterilmektedir: Sıradan matematiğin aksiyomatik bir sisteminde, "Σ(10 ↑↑ 10) = n " biçiminde doğru ama kanıtlanamaz bir cümle vardır ve sonsuz sayıda doğru- ancak "Σ(10 ↑↑ 10) < n " biçimindeki kanıtlanamayan cümleler .)
Maksimum vardiya fonksiyonu S
İşlev Σ ek olarak, [1962] adlı Radó Turing makineleri BB-sınıfı için bir aşırı işlev kişiye en kaymalar işlev , S , aşağıdaki gibi tanımlanmıştır:
- s ( M ) = kaydırma sayısıdır M herhangi biri için, kesilmeden önce yapar M içinde E , n ,
- S ( n ) = maks{ s ( M ) | M ∈ E n } = Duran herhangi bir n -durumlu 2 sembollü Turing makinesi tarafından yapılan en büyük kaydırma sayısı .
Bu Turing makinelerinin her geçişte veya "adımda" (Durma durumuna geçiş dahil) bir kaymaya sahip olması gerektiğinden, maksimum vardiya işlevi aynı zamanda bir maksimum adım işlevidir.
Radó, S'nin hesaplanamaz olduğunu gösterdi , aynı nedenle Σ hesaplanamaz - herhangi bir hesaplanabilir işlevden daha hızlı büyür. Bunu basitçe, her n , S ( n ) ≥ Σ( n ) için not ederek kanıtladı . Her vardiya bant üzerine 0 veya 1 yazabilirken, Σ 1 yazan vardiyaların bir alt kümesini, yani Turing makinesi durduğunda üzerine yazılmamış olanları sayar; sonuç olarak, S , en az Σ kadar hızlı büyür; bu, herhangi bir hesaplanabilir fonksiyondan daha hızlı büyüdüğü zaten kanıtlanmıştır.
Σ arasında aşağıdaki bağlantı S Lin ve Rado [tarafından kullanılan Turing makinesi Sorunların Bilgisayar alanında Σ (3) 6 = kanıtlamak için, 1965]: Belirli için , n ise, S ( n ) her zaman bilinen bir N -durum Turing makineleri (prensipte) S ( n ) adımlarına kadar çalıştırılabilir , bu noktada henüz durmamış herhangi bir makine asla durmaz. Bu noktada, bantta en fazla 1 saniye ile hangi makinelerin durduğunu gözlemleyerek (yani meşgul kunduzlar), bantlarından Σ( n ) değerini elde ederiz . Lin & Radó tarafından n = 3 durumu için kullanılan yaklaşım , S (3) = 21 olduğunu varsaymak, ardından esasen farklı olan tüm 3 durumlu makineleri 21 adıma kadar simüle etmekti . 21 adımda durmayan makinelerin davranışını analiz ederek, bu makinelerin hiçbirinin durmayacağını göstermeyi başardılar, böylece S (3) = 21 varsayımını kanıtladılar ve Σ(3) = 6 olduğunu belirlediler. az önce açıklanan prosedür.
Σ ve S ile ilgili eşitsizlikler , tüm n ≥ 1 için geçerli olan aşağıdakileri içerir ([Ben-Amram, et al., 1996]'dan itibaren) :
ve asimptotik olarak iyileştirilmiş bir sınır ([Ben-Amram, Petersen, 2002]'den): sabit bir c vardır , öyle ki tüm n ≥ 2 için ,
karesine yakın olma eğilimindedir ve aslında birçok makine daha az verir .
Σ ve S için bilinen değerler
2016 itibariyle Σ( n ) ve S ( n ) için fonksiyon değerleri sadece n < 5 için tam olarak bilinmektedir .
Mevcut (2018 itibariyle) 5 eyaletli meşgul kunduz şampiyonu üretir 4098 1s, kullanarak47 176 870 adım (1989'da Heiner Marxen ve Jürgen Buntrock tarafından keşfedilmiştir), ancak hiçbir zaman durmadığına inanılan, ancak durmadığı kanıtlanmayan 18 veya 19 (muhtemelen 10'un altında, aşağıya bakınız) makineler kalmıştır. sonsuz çalıştırın. Skelet, 42 veya 43 kanıtlanmamış makine listeler, ancak 24'ü zaten kanıtlanmış. Kalan makineler 81,8 milyar adıma simüle edildi, ancak hiçbiri durdurulmadı. Daniel Briggs ayrıca bazı makineleri kanıtladı. Başka bir kaynak, 98 makinenin kanıtlanmadığını söylüyor. Tutukluların bir analizi var. Bu nedenle, Σ(5) = 4098 ve S(5) = 47176870 olması muhtemeldir, ancak bu kanıtlanmamıştır ve herhangi bir gecikme olup olmadığı bilinmemektedir (2018 itibariyle). Şu anda rekor 6 eyalet şampiyonu üzerinde üretiyor3.515 × 10 18 267 1s (tam olarak (25×4 30341 +23)/9), üzerinde7.412 × 10 36 534 adım (Pavel Kropitz tarafından 2010'da bulundu). Yukarıda belirtildiği gibi, bunlar 2 sembollü Turing makineleridir.
6 durumlu makinenin basit bir uzantısı, 10 10 10 10'dan fazla yazacak 7 durumlu bir makineye yol açar.18 705 353 1s kasete, ancak şüphesiz çok daha yoğun 7 durumlu makineler var. Ancak, diğer meşgul kunduz avcıları farklı makine setlerine sahiptir.
Milton Green, 1964 tarihli "İkili Turing Makineleri için Rado'nun Sigma İşlevinde Bir Alt Sınır" adlı makalesinde, bir dizi Turing makinesi inşa etti.
burada ↑, Knuth yukarı ok gösterimidir ve A , Ackermann'ın işlevidir .
Böylece
(3 3 3 ile = 7 625 597 484 987 üstel kulede terim) ve
burada g 1 sayısı , Graham'ın sayısını tanımlayan dizideki muazzam başlangıç değeridir .
1964'te Milton Green, Anahtarlama devresi teorisi ve mantıksal tasarım üzerine 1964 IEEE sempozyumunun tutanaklarında yayınlanan Meşgul Kunduz işlevi için bir alt sınır geliştirdi. Heiner Marxen ve Jürgen Buntrock bunu "önemsiz (ilkel özyinelemeli olmayan) bir alt sınır" olarak tanımladı. Bu alt sınır hesaplanabilir ancak n cinsinden tek bir ifade olarak ifade edilemeyecek kadar karmaşıktır. n=8 olduğunda yöntem Σ(8) ≥ 3 × (7 × 3 92 - 1) / 2 ≈ 8.248×10 44 verir .
Mevcut alt sınırlardan şu şekilde türetilebilir:
Buna karşılık, Σ(6) üzerindeki en iyi akım (2018 itibariyle) alt sınırı Green'in formülüyle verilen alt sınırdan daha büyük olan 10 18 267 , 3 3 = 27 (karşılaştırıldığında çok küçük). Aslında, alt sınırdan çok daha büyüktür: 3 ↑↑ 3 = 3 3 3 =7 625 597 484 987 , Green'in Σ(8) için ilk alt sınırıdır ve ayrıca ikinci alt sınırdan çok daha büyüktür: 3×(7×3 92 −1)/2.
Σ(7) aynı şekilde mevcut ortak alt sınırdan 3 31 (yaklaşık 618 trilyon) çok, çok daha büyüktür , dolayısıyla ikinci alt sınır da çok, çok zayıftır.
S ( n ) ve Σ( n )' nin hesaplanamazlığının kanıtı
Varsayalım ki S ( n ) hesaplanabilir bir fonksiyonudur ve izin evals değerlendirilmesi, bir TM ifade S ( n ). n 1s olan bir bant verildiğinde, bant üzerinde S ( n ) 1s üretecek ve sonra duracaktır . Let Temiz başlangıçta kasete yazılı 1'lerin dizisini temizleme Turing makinesi belirtir. Let Çift fonksiyonunu değerlendiren Turing makinesi belirtmek n + n . n 1'li bir bant verildiğinde, bant üzerinde 2 n 1 üretecek ve sonra duracaktır . Bize kompozisyon yaratalım Çift | Değerlendirme | Temizleyin ve bu makinenin durum sayısı n 0 olsun . Let Create_n 0 belirtmektedir oluşturma Turing makinesi , n 0 , başlangıçta boş bir banda 1s. Bu makine için önemsiz bir şekilde inşa edilebilir , n 0 durumları (durum i 1 yazar, baş doğru hareket eder ve devlet geçer i durum hariç, 1 + n, 0 , durur). Let , N toplamı belirtmektedir , n 0 + n 0 .
Let bads yapıyı ifade Create_n 0 | Çift Kişilik | Değerlendirme | Temiz . Bu makinenin N durumu olduğuna dikkat edin . Başlangıçta boş bir bantla başlayarak, önce n 0 1'lik bir dizi oluşturur ve ardından bunu ikiye katlayarak N 1'lik bir dizi oluşturur . Ardından BadS , bant üzerinde S ( N ) 1'ler üretecek ve sonunda tüm 1'leri temizleyecek ve sonra duracaktır. Ancak temizleme aşaması en azından S ( N ) adımlarını sürdürecektir , bu nedenle BadS'nin çalışma süresi S ( N )' den kesinlikle daha büyüktür , bu da S ( n ) fonksiyonunun tanımına aykırıdır .
Σ( n )' nin hesaplanamazlığı da benzer şekilde kanıtlanabilir. Yukarıdaki kanıtta , EvalS makinesinin EvalΣ ve Clean with Increment ile değiştirilmesi gerekir - basit bir TM, bantta ilk 0'ı arar ve 1 ile değiştirir.
S ( n )' nin hesaplanamazlığı , boş bant durma problemine referansla da belirlenebilir. Boş bant durdurma problemi, herhangi bir Turing makinesinin boş bir bant üzerinde başlatıldığında durup durmayacağına karar verme problemidir. Boş bant durdurma sorunu, standart durdurma sorununa eşdeğerdir ve dolayısıyla aynı zamanda hesaplanamaz. S ( n ) hesaplanabilir olsaydı , boş bant durma problemini S ( n ) adımları için n durumlu herhangi bir Turing makinesini çalıştırarak çözebilirdik ; hala durmadıysa, asla durmayacaktır. Dolayısıyla, boş bant durdurma problemi hesaplanabilir olmadığından, S ( n )'nin de aynı şekilde hesaplanamaz olması gerektiği sonucu çıkar.
genellemeler
Herhangi bir hesaplama modeli için meşgul kunduzun basit analogları vardır. Örneğin, n durumlu ve m sembollü Turing makinelerine genelleme , aşağıdaki genelleştirilmiş meşgul kunduz fonksiyonlarını tanımlar :
- Σ( n , m ): bir n -durumu tarafından yazdırılabilen sıfır olmayan en büyük sayı , m -sembol makinesi , durmadan önce başlangıçta boş bir bantta başlatılır ve
- S ( n , m ): Durmadan önce başlangıçta boş bir bantta başlatılan bir n durumlu , m -sembol makinesi tarafından atılan en fazla adım sayısı .
Örneğin, şimdiye kadar bulunan en uzun süre çalışan 3 durumlu 3 sembollü makine çalışır Durmadan önce 119 112 334 170 342 540 adım. Her adımda bant değerini tersine çevirme özelliğine sahip en uzun çalışan 6 durumlu, 2 sembollü makine6147 1s sonra47 339 970 adım. Yani S RTM (6) ≥47 339 970 ve Σ RTM (6) ≥6147 .
Meşgul kunduz işlevini birden fazla boyuta genişleterek daha da genelleştirmek mümkündür.
Benzer şekilde , belirli bir komut sayısı için, durma sırasında herhangi bir kayıtta bulunabilecek en büyük sayı olarak kayıt makineleri için Σ işlevine bir analog tanımlayabiliriz .
Kesin değerler ve alt sınırlar
Aşağıdaki tablo , genelleştirilmiş meşgul kunduz problemleri için S ( n , m ) ve Σ( n , m ) için kesin değerleri ve bilinen bazı alt sınırları listeler . Not: "?" olarak listelenen girişler soldan ve yukarıdan tüm girişlerin maksimumu ile aşağıdan sınırlandırılır. Bu makineler ya araştırılmamış ya da daha sonra daha küçük bir makine tarafından aşılmıştır.
Bu değerlere ulaşan Turing makineleri Pascal Michel'in web sayfasında mevcuttur. Bu web sitelerinin her biri ayrıca Turing makinelerinin bazı analizlerini ve kesin değerlerin kanıtlarına referanslar içerir.
S( n , m ) değerleri nm2 durumlu 3 durumlu 4 durumlu 5 durumlu 6-devlet 7-devlet 2 sembol 6 21 107 47 176 870 ? > 7.4 × 10 36 534 > 10 10 10 1018 705 353 3-sembol 38 ≥ 119 112 334 170 342 540 > 1.0 × 10 14 072 ? ? ? 4 sembol ≥ 3 932 964 > 5,2 × 10 13 036 ? ? ? ? 5 sembol > 1.9 × 10 704 ? ? ? ? ? 6-sembol > 2.4 × 10 9866 ? ? ? ? ? Σ( n , m ) değerleri nm2 durumlu 3 durumlu 4 durumlu 5 durumlu 6-devlet 7-devlet 2 sembol 4 6 13 4098 ? > 3.5 × 10 18 267 > 10 10 10 1018 705 353 3-sembol 9 ≥ 374 676 383 > 1,3 × 10 7036 ? ? ? 4 sembol ≥ 2050 > 3,7 × 10 6518 ? ? ? ? 5 sembol > 1,7 × 10 352 ? ? ? ? ? 6-sembol > 1.9 × 10 4933 ? ? ? ? ?
Belirsiz Turing makineleri
| P | adımlar | devletler |
|---|---|---|
| 1 | 2 | 2 |
| 2 | 4 | 4 |
| 3 | 6 | 7 |
| 4 | 7 | 11 |
| 5 | 8 | 15 |
| 6 | 7 | 18 |
| 7 | 6 | 18 |
Problem, tüm dallarda en fazla durum sayısına sahip sistemi veya en uzun adım sayısına sahip şubeyi arayarak Nondeterministik Turing makinelerine genişletilebilir . Belirli bir NDTM'nin durup durmayacağı sorusu hala hesaplama açısından indirgenemez ve bir NDTM meşgul kunduz bulmak için gereken hesaplama, dikkate alınması gereken birden çok dal olduğundan, deterministik durumdan önemli ölçüde daha büyüktür. p vakası veya kuralı olan 2 durumlu, 2 renkli bir sistem için, sağdaki tablo durmadan önceki maksimum adım sayısını ve NDTM tarafından oluşturulan maksimum benzersiz durum sayısını verir.
Uygulamalar
Oldukça zorlu bir matematiksel oyun oluşturmaya ek olarak , meşgul kunduz işlevleri, saf matematik problemlerini çözmek için tamamen yeni bir yaklaşım sunar. Matematikteki birçok açık problem teoride olabilir, ancak pratikte değil, yeterince büyük bir n için S ( n )' nin değeri verilen sistematik bir şekilde çözülebilir .
Herhangi düşünün varsayım olabilir çürütüldü bir aracılığı kar¸ıt bir arasında sayılabilir davaların sayısında (örn Goldbach en varsayım ). Artan değerler için bu varsayımı sırayla test eden bir bilgisayar programı yazın. Goldbach varsayımı durumunda, her çift sayıyı ≥ 4 sıralı olarak ele alır ve iki asal sayının toplamı olup olmadığını test ederiz. Bu programın n- durumlu bir Turing makinesinde simüle edildiğini varsayalım . Bir karşı örnek bulursa (örneğimizde iki asal sayının toplamı olmayan bir çift sayı ≥ 4), durur ve bunu belirtir. Ancak varsayım doğruysa, programımız asla durmaz. (Bu program yalnızca bir karşı örnek bulduğunda durur .)
Şimdi, bu program n- durumlu bir Turing makinesi tarafından simüle edilir , bu nedenle S ( n ) 'yi biliyorsak , makineyi bu kadar çok adımda çalıştırarak durup durmayacağına (sınırlı bir süre içinde) karar verebiliriz. Ve eğer S ( n ) adımlarından sonra makine durmazsa, asla durmayacağını ve dolayısıyla verilen varsayıma karşı hiçbir örnek olmadığını (yani iki asal sayının toplamı olmayan çift sayılar olmadığını) biliriz. Bu, varsayımın doğru olduğunu kanıtlayacaktır.
Böylece S ( n ) için özel değerler (veya üst sınırlar) matematikte (teoride) birçok açık problemi sistematik olarak çözmek için kullanılabilir. Ancak, meşgul kunduz sorunuyla ilgili mevcut sonuçlar, bunun iki nedenden dolayı pratik olmayacağını gösteriyor:
- Meşgul kunduz işlevi (ve maksimum kaydırma işlevi) için değerleri kanıtlamak son derece zordur. Kullanışlı bir makine yapmak için muhtemelen en az 20-50 duruma ihtiyaç duyulurken, yalnızca beşten daha az durumu olan son derece küçük makineler için kanıtlanmıştır. Ayrıca, S ( n )'nin bilinen her kesin değeri, her n- durumlu Turing makinesini numaralandırarak ve her birinin durup durmadığını kanıtlayarak kanıtlandı. Bir hesaplamak zorunda kalacak S ( n aslında yararlı olması için bazı daha az doğrudan yöntemle).
- Ancak S ( n ) hesaplamak için daha iyi bir yol bulunsa bile , meşgul kunduz fonksiyonunun (ve maksimum kaydırma fonksiyonunun) değerleri çok büyük, çok hızlı olur. S (6) > 1036 534 , tamamlanmaya kadar simüle edebilmek için zaten özel desen tabanlı hızlandırma gerektirir. Benzer şekilde, S (10) > Σ(10) > 3 ↑↑↑ 3'ün devasa bir sayı olduğunu ve S (17) > Σ(17) > G'nin, burada G'nin Graham'ın sayısıolduğunu biliyoruz- muazzam bir sayı. Bu nedenle, diyelim ki S (30) olduğunu bilsek bile, herhangi bir makineyi bu sayıda adım çalıştırmak tamamen mantıksızdır. Evrenin bilinen kısmında S (6) işlemlerinibiledoğrudangerçekleştirebilecek yeterli hesaplama kapasitesi yoktur.
Önemli örnekler
Bir 748-durum ikili Turing makinesi durur şekilde inşa edilmiştir IFF ZFC tutarsız. Riemann hipotezinin yanlış olması durumunda onu durduran 744 durumlu bir Turing makinesi yapılmıştır . Goldbach'ın varsayımının yanlış olması durumunda durduran 43 durumlu bir Turing makinesi inşa edildi ve bu varsayım için 27 durumlu bir makine önerildi, ancak henüz doğrulanmadı.
Bir 15-durum Turing makinesi durur şekilde inşa edilmiştir IFF formüle, aşağıdaki varsayım Paul Erdös 1979 yanlıştır: her n için> 8 2 tabanı 3 temsili en az bir basamak 2 vardır n .
Örnekler
Bunlar, Σ(1) ve S (1), Σ(2) ve S (2), Σ(3) (ancak S (3) değil), Σ(4) ve S üreten Turing makineleri için kural tablolarıdır. (4) ve Σ(5) ve S (5) ve Σ(6) ve S (6) için en iyi bilinen alt sınır . Diğer görselleştirmeler için
Tablolarda sütunlar mevcut durumu, satırlar ise banttan okunan mevcut sembolü temsil eder. Her tablo girişi, bant üzerine yazılacak sembolü, hareket yönünü ve yeni durumu (bu sırayla) gösteren üç karakterden oluşan bir dizedir. Durma durumu H olarak gösterilir .
Her makine, A durumunda , tüm 0'ları içeren sonsuz bir bantla başlar . Bu nedenle, banttan okunan ilk sembol 0'dır.
Sonuç tuşu: ( üstü çizili konumda başlar, altı çizili konumda durur )
1 durumlu, 2 sembollü meşgul kunduz A 0 1R H 1 (kullanılmamış)
Sonuç: 0 0 1 0 0 (1 adım, toplamda bir "1")
2 durumlu, 2 sembollü meşgul kunduz A B 0 1R B 1L A 1 1L B 1R H
Sonuç: 0 0 1 1 1 1 0 0 (6 adım, toplam dört "1")
3 durumlu, 2 sembollü meşgul kunduz A B C 0 1R B 0R C 1L C 1 1R H 1R B 1L A
Sonuç: 0 0 1 1 1 1 1 1 0 0 (14 adım, toplamda altı "1").
Önceki makinelerden farklı olarak, bu yalnızca Σ için meşgul bir kunduzdur, ancak S için değildir . ( S (3) = 21.)
4 durumlu, 2 sembollü meşgul kunduz A B C NS 0 1R B 1L A 1R H 1R D 1 1L B 0L C 1L D 0R bir
Sonuç: 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 adım, toplam on üç "1")
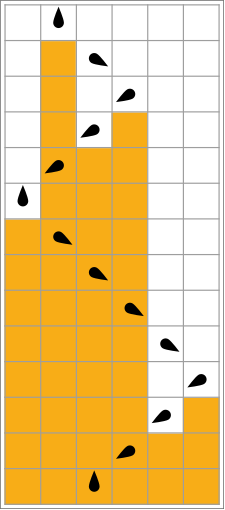
mevcut 5 durumlu, 2 sembollü en iyi yarışmacı (olası meşgul kunduz) A B C NS E 0 1R B 1R C 1R D 1L A 1R H 1 1L C 1R B 0L E 1L D 0L bir
Sonuç: 47.176.870 adımda serpiştirilmiş 8191 "0" ile 4098 "1".
Sağdaki resimde, bu çözümün niteliksel olarak bazı hücresel otomatların evrimine nasıl benzediğine dikkat edin .
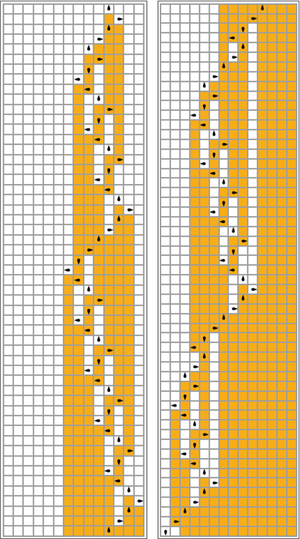
mevcut 6 durumlu, 2 sembollü en iyi yarışmacı A B C NS E F 0 1R B 1R C 1L D 1R E 1L A 1L H 1 1L E 1R F 0R B 0L C 0R D 1R C
Sonuç: × 10 ≈3.515 18267 "1" ≈7.412 × 10 s 36534 adımlar.
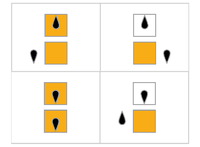
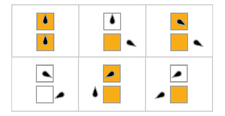
görselleştirmeler
Aşağıdaki tabloda, her meşgul kunduz için kurallar (Σ 'yi maksimize ederek), bant üzerinde "1"e karşılık gelen turuncu kareler ve "0"a karşılık gelen beyaz ile görsel olarak temsil edilmektedir. Başın konumu, durumu temsil eden başın yönü ile siyah oval ile gösterilir. Bireysel bantlar yatay olarak düzenlenir, zamanla dikey olarak ilerler. Durma durumu, bir durumu kendisine eşleyen bir kuralla temsil edilir (kafa hareket etmez).
Ayrıca bakınız
Notlar
- ^ a b Radó, Tibor (Mayıs 1962). "Hesaplanamayan işlevler hakkında" (PDF) . Bell Sistemi Teknik Dergisi . 41 (3): 877-884. doi : 10.1002/j.1538-7305.1962.tb00480.x .
- ^ Chaitin (1987)
- ^ Adam Yedidia ve Scott Aaronson (Mayıs 2016). Davranışı Küme Teorisinden Bağımsız olan Nispeten Küçük Bir Turing Makinesi (Teknik Rapor). MİT. arXiv : 1605.04343 . Bibcode : 2016arXiv160504343Y .
- ^ Aron, Yakup. "Matematik yanlış olmadığı sürece bu Turing makinesi sonsuza kadar çalışmalı" . 2016-09-25 alındı .
- ^ a b 3 Mayıs tarihli sürüm 7918 durum içeriyordu: "8000'inci Meşgul Kunduz sayısı ZF küme teorisini atlatıyor" . Shtetl için Optimize Edilmiş blog . 2016-05-03 . 2016-09-25 alındı .
- ^ a b c "Üç duyuru" . Shtetl için Optimize Edilmiş blog . 2016-05-03 . 2018-04-27 alındı .
- ^ "GitHub - boğaz / metamath-turing-makineleri: Metamath geçirmez numaralandırıcılar ve diğer şeyler" . 2019-02-13.
- ^ "Meşgul Kunduz Sınırı" (PDF) .
- ^ "Meşgul Kunduz sorunu için İskelet sayfası" . iskelet.ludost.net .
- ^ Turing: Busy Beaver of 5'i Bitirecek Bir Proje
- ^ "Meşgul Kunduz Sorunu: YENİ BİR BİN YILLIK SALDIRI" .
- ^ a b Wolfram, Stephen (4 Şubat 2021). "Çok Yönlü Turing Makineleri" . www.wolframphysics.org .
- ^ Chaitin 1987
- ^ Lloyd 2001. Evrenin Hesaplamalı Kapasitesi .
- ^ a b c Pavlus, John (10 Aralık 2020). "En Yavaş Bilgisayar Programları Matematiğin Temel Sınırlarını Nasıl Aydınlatıyor" . Quanta Dergisi . 2020-12-11 alındı .
- ^ Tristan Sérin ve Damien Woods (Temmuz 2021). Meşgul kunduz değerlerinin BB(15) ve BB(5,4) bilmenin sertliği üzerine (Teknik Rapor). Maynooth Üniversitesi. arXiv : 2107.12475 .
- ^ Erdos, Paul (1979). "Sayı teorisinde bazı geleneksel olmayan problemler" . Matematik. Mag. 52 (2): 67–70. doi : 10.1080/0025570X.1979.11976756 .
- ^ Lin, Shen; Rado, Tibor (Nisan 1965). "Turing makinesi problemlerinin bilgisayar çalışmaları" . ACM Dergisi . 12 (2): 196–212. doi : 10.1145/321264.321270 . S2CID 17789208 .
Referanslar
-
Radó, Tibor (Mayıs 1962). "Hesaplanamayan işlevler hakkında" (PDF) . Bell Sistemi Teknik Dergisi . 41 (3): 877-884. doi : 10.1002/j.1538-7305.1962.tb00480.x .
- Radó'nun meşgul kunduz problemini ilk tanımladığı ve hesaplanamaz olduğunu ve herhangi bir hesaplanabilir fonksiyondan daha hızlı büyüdüğünü kanıtladığı yer burasıdır.
-
Lin, Shen; Radó, Tibor (Nisan 1965). "Turing Makinesi Problemlerinin Bilgisayar Çalışmaları" . ACM Dergisi . 12 (2): 196–212. doi : 10.1145/321264.321270 . S2CID 17789208 .
- Bu makalenin sonuçları, Lin'in 1963'te Radó'nun rehberliğinde yaptığı doktora tezinde kısmen ortaya çıkmıştı. Lin & Radó, 21 adımda durmayan tüm 3 durumlu 2 sembollü Turing Makinelerinin asla durmayacağını kanıtlayarak Σ(3) = 6 ve S (3) = 21 olduğunu kanıtlıyor. (Çoğu bir bilgisayar programı tarafından otomatik olarak kanıtlanmıştır, ancak 40'ı insan denetimiyle kanıtlanmıştır.)
-
Brady, Allen H. (Nisan 1983). " Dört durumlu Turing makineleri için Rado'nun hesaplanamayan fonksiyonu Σ( k ) değerinin belirlenmesi " . Hesaplama Matematiği . 40 (162): 647-665. doi : 10.1090/S0025-5718-1983-0689479-6 . JSTOR 2007539 .
- Brady, Σ(4) = 13 ve S (4) = 107 olduğunu kanıtlar. Brady, durmayan 3 durumlu 2 sembollü Turing Makineleri için iki yeni kategori tanımlar: Noel Ağaçları ve Sayaçlar. 107 adımın üzerinde çalışan 27 makine dışında hepsinin sonsuz çalıştığı kanıtlanabilen Noel Ağaçları ve Sayaçların çeşitleri olduğunu kanıtlamak için bir bilgisayar programı kullanıyor. Son 27 makinenin (bekleme olarak anılır) durmadığı Brady'nin bizzat yaptığı kişisel incelemeyle kanıtlanmıştır.
-
Maclin, Rona; Stout, Quentin F. (Haziran 1990). "Basit makinelerin karmaşık davranışı" . Physica D: Doğrusal Olmayan Olaylar . 42 (1–3): 85–98. Bibcode : 1990PhyD...42...85M . doi : 10.1016/0167-2789(90)90068-Z . hdl : 2027.42/28528 .
- Machlin ve Stout, meşgul kunduz problemini ve meşgul kunduzları bulmak için kullanılan birçok tekniği tanımlar (4 durumlu ve 2 sembollü Turing Makinelerine uyguladıkları ve böylece Brady'nin kanıtını doğruladıkları). Chaitin'in durma olasılığının (Ω) bir varyantının nasıl tahmin edileceğini önerirler.
-
Marxen, Heiner; Buntrock, Jürgen (Şubat 1990). "Meşgul Kunduz 5'e Saldırmak" . EATCS Bülteni . 40 : 247–251. 2006-10-09 tarihinde kaynağından arşivlendi . 2020-01-19 alındı .
- Marxen ve Buntrock, Σ(5) ≥ 4098 ve S (5) ≥ olduğunu gösterir. 47 176 870 ve bu makineleri bulmak için kullandıkları yöntemi ayrıntılı olarak açıklayın ve diğerlerinin asla durmayacağını kanıtlayın.
-
Green, Milton W. (1964). İkili Turing Makineleri için Rado'nun Sigma İşlevinde Daha Düşük Bir Sınır . 1964 Anahtarlama Devresi Teorisi ve Mantıksal Tasarım Beşinci Yıllık Sempozyumu Bildiriler Kitabı . s. 91–94. doi : 10.1109/SWCT.1964.3 .
- Green, herhangi bir sayıda durum için makineleri yinelemeli olarak oluşturur ve puanlarını hesaplayan özyinelemeli işlevi sağlar (σ hesaplar), böylece Σ için bir alt sınır sağlar. Bu fonksiyonun büyümesi, Ackermann fonksiyonunun büyümesiyle karşılaştırılabilir .
-
Dewdney, Alexander K. (1984). "Meşgul kunduz için bir bilgisayar tuzağı, en çalışkan Turing makinesi". Bilimsel Amerikalı . 251 (2): 10–17.
- Meşgul kunduz programları Alexander Dewdney tarafından Scientific American , Ağustos 1984, sayfa 19-23, ayrıca Mart 1985 s. 23 ve Nisan 1985 s. 30 .
- Chaitin, Gregory J. (1987). "Meşgul Kunduz İşlevinin Hesaplanması" (PDF) . Kapakta, TM; Gopinath, B. (ed.). İletişim ve Hesaplamada Açık Sorunlar . Springer. s. 108–112. ISBN'si 978-0-387-96621-2.
-
Brady, Allen H. (1995). "Meşgul Kunduz Oyunu ve Hayatın Anlamı". Herken'de, Rolf (ed.). Evrensel Turing Makinesi: Yarım Yüzyıl Araştırması (2. baskı). Wien, New York: Springer-Verlag. s. 237–254. ISBN'si 978-3-211-82637-9.
- Burada (4 eyaletli ünlü) Brady, canavarın bazı tarihini anlatıyor ve arayışını "Meşgul Kunduz Oyunu" olarak adlandırıyor. Diğer oyunları anlatıyor (örneğin hücresel otomatlar ve Conway'in Game of Life ). "İki Boyutta Meşgul Kunduz Oyunu" (s. 247) özellikle ilgi çekicidir. 19 referans ile.
-
Booth, Taylor L. (1967). Sıralı Makineler ve Otomata Teorisi . New York: Wiley. ISBN'si 978-0-471-08848-6.
- Bkz. Bölüm 9, Turing Makineleri. Elektrik mühendisleri ve teknik uzmanlar için zor bir kitap. Turing Machines, durma problemine referansla özyineleme, kısmi özyinelemeyi tartışır. Booth'taki bir referans, meşgul kunduzu Rado'ya bağlar. Booth ayrıca Rado'nun meşgul kunduz problemini Bölüm 9, s. 3, 4, 5, 6 "ev sorunları"nda tanımlar. 396. Problem 3, "meşgul kunduz probleminin tüm n değerleri için... çözülemez olduğunu göstermektir."
-
Ben Amram, AM; Julstrom, BA; Zwick, U. (1996). "Meşgul Kunduzlar ve diğer yaratıklar üzerine bir not" . Matematiksel Sistemler Teorisi . 29 (4): 375–386. CiteSeerX 10.1.1.75.1297 . doi : 10.1007/BF01192693 . S2CID 30937913 .
- Σ ve S fonksiyonları arasındaki sınırlar .
-
Ben Amram, AM; Petersen, H. (2002). "Meşgul Kunduzlarla İlgili İşlevler için İyileştirilmiş Sınırlar". Hesaplama Sistemleri Teorisi . 35 : 1–11. CiteSeerX 10.1.1.136.5997 . doi : 10.1007/s00224-001-1052-0 . S2CID 10429773 .
- Geliştirilmiş sınırlar.
-
Lafitte, G.; Papazyan, Ç. (Haziran 2007). "Küçük Turing makinelerinin kumaşı". Gerçek Dünyada Hesaplama ve Mantık, Avrupa'da Hesaplanabilirlik Üzerine Üçüncü Konferansın Tutanakları . s. 219–227. CiteSeerX 10.1.1.104.3021 .
- Bu makale, 2 durumlu, 3 sembollü Turing makinelerinin tam bir sınıflandırmasını ve dolayısıyla (2, 3) meşgul kunduz için bir kanıt içerir: Σ(2, 3) = 9 ve S(2, 3) = 38.
- Boolos, George S.; Burgess, John P.; Jeffrey, Richard C. (2007). Hesaplanabilirlik ve Mantık (Beşinci baskı). Cambridge Üniversitesi Yayınları. ISBN'si 978-0-521-87752-7.
-
Kropitz, Pavel (2010). Problem Meşgul Kunduz (Lisans tezi) (Slovakça). Prag'daki Charles Üniversitesi.
- Bu, 31 adet 4 çekirdekli bilgisayarda paralel olarak çalıştırılan 5 durumlu ve 6 durumlu Turing makinelerini inceleyen deneylerin açıklaması ve son olarak 6 durumlu TM için en iyi sonuçların, fikirlerin, algoritmaların ve bunların uygulanmasının açıklamasıdır.
Dış bağlantılar
- Jürgen Buntrock ile birlikte 5 ve 6 durumlu bir Turing makinesi için yukarıda belirtilen kayıtları bulan Heiner Marxen'in sayfası .
- Pascal Michel'in en iyi sonuçları ve bazı analizleri de içeren meşgul kunduz sonuçlarına ilişkin Tarihsel araştırması .
- RTM sınıfının tanımı - Ters Turing Makineleri, TM'lerin basit ve güçlü alt sınıfı.
- Rensselaer RAIR Laboratuarında meşgul kunduz Problemi üzerine " Milenyum Saldırısı ". Bu çaba birkaç yeni kayıt buldu ve dörtlü formalizasyon için birkaç değer belirledi.
- Daniel Briggs'in 5 durumlu, 2 sembollü meşgul kunduz problemini çözmek için web sitesi arşivi ve forumu , Skelet (Georgi Georgiev) düzensiz makineler listesine dayanmaktadır .
- Aaronson, Scott (1999), En büyük sayıyı kim söyleyebilir?
- Weisstein, Eric W. "Meşgul Kunduz" . Matematik Dünyası .
- Meşgul Kunduz Turing Makineleri - Computerphile
- Pascal Michel. Meşgul Kunduz Yarışması: tarihsel bir anket . 70 sayfa. 2017. <hal-0039880v5>